Понятие вывода

Решение

Пример 8.4

Доказать, что из совокупности 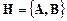можно вывести . Записать полученный вывод.

1. Так как по условию задачи формула принадлежит (), то по определению выводимой формулы

├ . (8.4.1)

2. Так как по условию задачи и формула принадлежит (),то по определению выводимой формулы

├ . (8.4.2)

3. На основании аксиомы II₃ 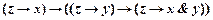и подстановки получим доказуемую формулу, которая выводима из по определению выводимой формулы (как конечная совокупность формул)

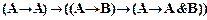├ . (8.4.3)

4. На основании аксиомы I₁ 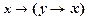и подстановки получим доказуемую формулу, которая выводима из по определению выводимой формулы (как конечная совокупность формул)

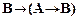├ . (8.4.4)

5. Так как формула 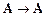, являющаяся частью формулы (8.4.3), является доказуемой формулой (см. пример 8.2), то

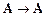├ . (8.4.5)

8. Из формул (8.4.3) и (8.4.5) по правилу заключения получим

,

├ ;├

├

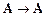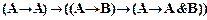
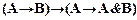
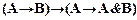├ . (8.4.6)

7. Из формул (8.4.2) и (8.4.4) по правилу заключения получим

,

├ ;├

├

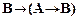
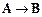
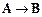├ . (8.4.7)

8. Из формул (8.4.6) и (8.4.7) по правилу заключения получим

,

├ ;├

├

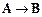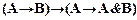
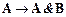
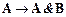├ . (8.4.8)

9. Наконец, из формул (8.4.1) и (8.4.8) по правилу заключения получим

,

├ ;├

├

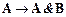
├ . (8.4.9)

Таким образом, доказано, что из совокупности 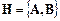можно вывести формулу .

Данный вывод можно привести в виде короткой записи, последовательно записывая формулы (8.4.1) – (8.4.9).

.

(8.4.10)

Отметим, что при доказательстве выводимости формулы из совокупности формул можно пользоваться не только основным правилом заключения, но и правилом сложного заключения (п. 8.1.3), применяя которое, формулу (8.4.9) можно получить из формул (8.4.5), (8.4.7), (8.4.1) и (8.4.3).

10. Формула (8.4.3) 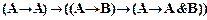доказуема. Поскольку в эту формулу входят доказуемые формулы, выводимые из совокупност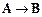и : (), () и , то, применяя правило сложного заключения 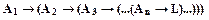, где 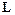доказуемая формула, получим, что и = 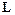тоже является доказуемой формулой, выводимой из совокупности .

Таким образом, и с помощью правила сложного заключения доказано, что из совокупности можно вывести формулу .

Данный вывод можно также привести в виде короткой записи, последовательно записывая формулы (8.4.1) – (8.4.5), (8.4.7), (8.4.9).

.

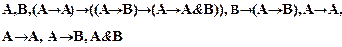(8.4.11)

Вывод из конечной совокупности формул – это всякая конечная последовательность формул , любой член которой удовлетворяет одному из следующих условий:

1) он является одной из формул совокупности ,

2) является доказуемой формулой,

3) получается по правилу заключения из двух любых предшествующих членов последовательности .

Как было показано в примере 8.4, выводом из совокупности формул 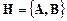является конечная последовательность формул (8.4.10) и (8.4.11).

Из определений выводимой формулы и вывода из совокупности формул следуют свойства вывода:

1. Всякий начальный отрезок вывода из совокупности есть вывод из .

Действительно, все формулы начального отрезка вывода удовлетворяют определению вывода.

2. Если между двумя соседними членами вывода из (или в начале, или в конце его) вставить некоторый вывод из , то полученная новая последовательность формул будет выводом из .

Например, если совокупности формул 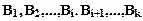и являются выводами из , то совокупность по определению вывода является выводом из .

3. Всякий член вывода из совокупности является формулой, выводимой из .

Всякий вывод из является выводом его последней формулы.

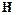4. Если , то всякий вывод из является выводом из .

5. Для того чтобы формула была выводима из совокупности 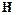, необходимо и достаточно, чтобы существовал вывод этой формулы из .

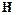Дата добавления: 2017-02-01