
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Учебно-методическое обеспечение
|
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
Задания к выполнению работы
1. Какие из следующих выражений являются формулами исчисления высказываний:
1)  ;
;
2) 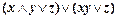 ;
;
3) 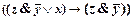 ;
;
4) 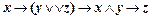 ;
;
5) 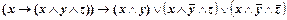 ;
;
6) 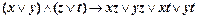 ;
;
7)  ;
;
8)  ;
;
9)  .
.
2.2. Выписать все подформулы формул:
1)  ;
;
2) 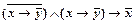 ;
;
3) 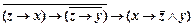 ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7) 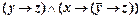 ;
;
8)  ;
;
9) 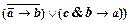 .
.
2.3. Для формул 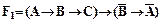 ,
,  ,
, 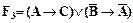 ,
,  записать результаты каждой из следующих подстановок:
записать результаты каждой из следующих подстановок:
1)  ; 2)
; 2) 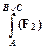 ; 3)
; 3) 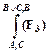 ; 4)
; 4) 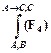 ;
;
5)  ; 6)
; 6) 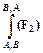 ; 7)
; 7)  ; 8)
; 8)  .
.
Решение примера 1.
 .
.
2.4. Показать, доказуемость нижеследующих формул, применяя правило подстановки:
16)  ;
;
17)  ;
;
18)  ;
;
19) 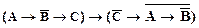 ;
;
20)  ;
;
21) 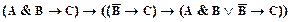 ;
;
22) 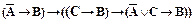 ;
;
23)  .
.
Решение примера 1.
Для решения подобных примеров необходимо подобрать соответствующую аксиому из четырех групп аксиом, которые все являются доказуемыми формулами, и найти такие подстановки переменных, которые приведут к необходимой формуле. В частности для данного примера необходимо взять аксиому I1 и вместо  надо подставить выражение
надо подставить выражение  , а вместо
, а вместо  –
– 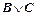
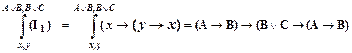 .
.
2.5. Показать, доказуемость нижеследующих формул, применяя правило подстановки и правило заключения:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5) 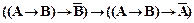 ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  .
.
Решение примера 1.
Для решения подобных примеров необходимо подобрать соответствующую аксиому из четырех групп аксиом, таким образом, чтобы после проведения подстановки можно было применить либо правило заключения
|
├В
либо правило сложного заключения
|
 ├
├  ├
├ 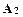 ,…,├
,…,├  ;├
;├ 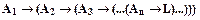
├ 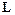
1) Возьмем аксиому I1 
и сделаем в ней подстановку  . Получим доказуемую формулу
. Получим доказуемую формулу
├ 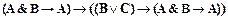 ,
,
в которой можно выделить две части: доказуемую формулу  = ├
= ├ 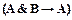 (аксиома II1
(аксиома II1  ) и еще недоказанную формулу
) и еще недоказанную формулу  .
.
2) Применяя правило заключения,
|
 ├
├ 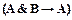 ; ├
; ├ 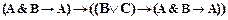
├ 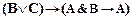
получим доказуемую формулу ├ 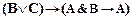 .
.
2.6. Показать, доказуемость нижеследующих формул, применяя производные правила вывода.
1)  ;
;
2) 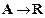 ;
;
3)  ;
;
4) 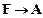 ;
;
5)  ;
;
6) 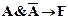 ;
;
7) 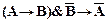 ;
;
8) 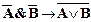 ;
;
9) 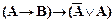 .
.
Решение примера 1.
Для решения подобных примеров необходимо так же, как и в предыдущих заданиях, подобрать соответствующую аксиому из четырех групп аксиом, произвести подстановку таким образом, чтобы можно было применить производные правила вывода, после осуществления которых применяют либо правило заключения, либо правило сложного заключения.
1) Возьмем аксиому III3 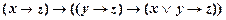
и сделаем подстановку 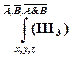 , получим доказуемую формулу ├
, получим доказуемую формулу ├  .
.
2) Покажем доказуемость формул 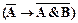 и
и  . Для этого берем аксиомы II1
. Для этого берем аксиомы II1  и II2
и II2  и применяем к ним подстановку
и применяем к ним подстановку  и
и 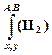 , получим ├
, получим ├  и ├
и ├ 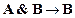 . Далее применяем к ним правило контрпозиции
. Далее применяем к ним правило контрпозиции
|
 , ├
, ├ 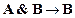

 ├
├  ├
├ 
получим доказуемые формулы ├  и ├
и ├  .
.
3) Теперь можно применить правило сложного заключения
 ├
├  , ├
, ├  ; ├
; ├  .
.
├ 
Получим доказуемую формулу  .
.
2.7. Доказать, что
1) 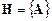 ├
├  ;
;
2)  ├
├  ;
;
3)  ├
├  ;
;
4) 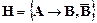 ├
├  ;
;
5)  ├
├ 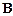 ;
;
6) 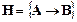 ├
├  ;
;
7) 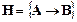 ├
├ 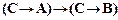 ;
;
8) 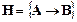 ├
├  ;
;
9) 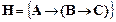 ├
├ 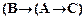 ;
;
10) 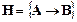 ├
├  .
.
Решение примера 1.
1) Так как по условию задачи формула  принадлежит
принадлежит  (
( ), то по определению выводимой формулы она доказуема
), то по определению выводимой формулы она доказуема
 ├
├  .
.
2) На основании аксиомы I1 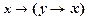 и подстановки
и подстановки 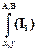 получим доказуемую формулу, которая выводима из
получим доказуемую формулу, которая выводима из  по определению выводимой формулы
по определению выводимой формулы
├  .
.
3) Применяя правило заключения
|
 ├
├ 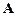 ; ├
; ├ 
├ 
получим доказуемую формулу
├  .
.
В итоге запишем вывод из  :
: 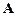 ,
,  ,
,  .
.
Решение примера 2.
1) Так как по условию задачи совокупности  принадлежат доказуемые формулы
принадлежат доказуемые формулы  и
и 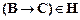 , то, применяя правило силлогизма
, то, применяя правило силлогизма
|
├ А → С
получим доказуемую формулу  . Вывод из
. Вывод из  запишется так:
запишется так:  :
: 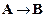 ,
,  ,
, 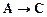 .
.
2.8. Показать доказуемость нижеследующих формул, применяя обобщенную теорему дедукции:
1)  ;
;
2) 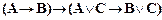 ;
;
3) 
Решение примера 1.
Возьмем совокупность формул

и докажем, что  ├
├  . Запишем для этого вывод из
. Запишем для этого вывод из  :
: 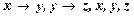 . Тогда по обобщенной теореме дедукции, заключающейся в том, что если существует доказуемая формула
. Тогда по обобщенной теореме дедукции, заключающейся в том, что если существует доказуемая формула  , выводимая из объединения совокупностей
, выводимая из объединения совокупностей  , то существует и доказуемая формула
, то существует и доказуемая формула  , выводимая из совокупности
, выводимая из совокупности 
|

 ├
├ 
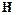 ├
├ 
получим ├  .
.
2.9. Показать, что справедливы законы логики (доказуемы формулы):
1)  ; 2)
; 2)  ; 3)
; 3) 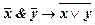 .
.
Решение примера 1.
1) Сделаем подстановки в аксиомы I1  и IV1
и IV1 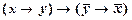
 и
и 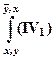 .
.
В результате получим доказуемые формулы
├  ,
,
├ 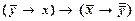 .
.
2) Из этих формул по правилу силлогизма (е сли доказуемы формулы А → В и В → С, то доказуема иформула А → С) следует:
├  .
.
3) Используя закон соединения посылок (если формула  доказуема, то доказуема и формула
доказуема, то доказуема и формула 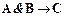 , полученная из исходной путем объединения посылок
, полученная из исходной путем объединения посылок  и
и 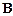 ), получим
), получим
├  .
.
4) Используем правило снятия двойного отрицания (е сли доказуема формула  , то доказуема формула
, то доказуема формула  , и е сли доказуема формула
, и е сли доказуема формула  , то доказуема формула
, то доказуема формула 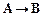 ), получим
), получим
├ 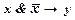 .
.
5) И в итоге применим правило разъединения посылок (е сли формула 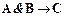 доказуема, то доказуема и формула
доказуема, то доказуема и формула  , полученная из исходной путем разъединения посылок
, полученная из исходной путем разъединения посылок  и
и 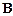 ), получим доказуемую формулу
), получим доказуемую формулу
├ 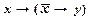 .
.
2.10. Используя правила перестановки посылок, соединения посылок и разъединения посылок, доказать, что
1) ├  ;
;
2) ├  ;
;
3) ├  .
.
2.11. Доказать производные правила вывода:
|
|
|
|
|
|
 ├
├ 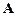 ├
├ 


 ├
├ 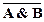 ├
├  ├
├ 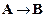


|
|
|
|
|
|
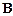 ├
├ 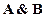 ├
├ 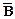
 ├
├ 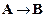 ├
├ 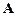 ├
├ 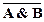
|

|
|
|
|
|
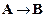 , ├
, ├ 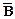 ├
├ 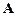 , ├
, ├ 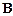 ├
├  , ├
, ├ 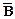

 ├
├  ├
├ 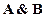 ├
├ 
|
|
|
|
|
|
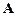 , ├
, ├ 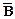 ├
├ 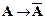 ├
├ 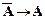


 ├
├ 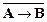 ├
├  ├
├ 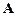
|
|
|

|
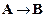 , ├
, ├ 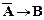 ├
├ 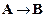 , ├
, ├ 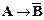
 ├
├ 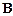 ├
├ 
Решение примера 1.
1) По условию формула  доказуема, то есть ├
доказуема, то есть ├  .2) Используем аксиому II1
.2) Используем аксиому II1  и подстановку
и подстановку  ,получим ├
,получим ├  .
.
3) Применим к данной формуле правило контрпозиции (е сли доказуема формула  , то доказуема формула
, то доказуема формула 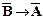 ). Получим
). Получим
├  .
.
4) Из формул п. 1 и п. 3 по правилу заключения (е сли формулы  и
и  доказуемы, то формула
доказуемы, то формула  также доказуема) получим ├
также доказуема) получим ├ 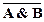 . Таким образом, пример 1 доказан.
. Таким образом, пример 1 доказан.
2.12. Дана формула  и наборы значений переменных. Записать вывод формулы
и наборы значений переменных. Записать вывод формулы 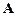 или ее отрицания из соответствующей совокупности формул
или ее отрицания из соответствующей совокупности формул
1) 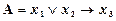 . Наборы переменных: 1) (0, 0, 1); 2) (1, 0, 0).
. Наборы переменных: 1) (0, 0, 1); 2) (1, 0, 0).
2)  . 1) (1, 1, 1); 2) (1, 0, 1); 3) (0, 1, 0).
. 1) (1, 1, 1); 2) (1, 0, 1); 3) (0, 1, 0).
3) 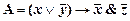 . 1) (1, 0, 0); 2) (0, 1, 1).
. 1) (1, 0, 0); 2) (0, 1, 1).
Решение примера 1.
1)  ├
├  . Вывод:
. Вывод:
 .
.
2) 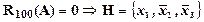 ├
├  . Вывод:
. Вывод:
 .
.
1. В чем заключается отличие исчисления высказываний от алгебры высказываний?
2. Из чего состоит алфавит исчисления высказываний?
3. Дать определение формулы исчисления высказываний.
4. Дать понятие подформулы исчисления высказываний.
5. Привести первую и вторую группу аксиом.
6. Привести третью и четвертую группу аксиом.
7. Сформулировать правило подстановки и правило заключения.
8. Определение доказуемой формулы.
9. Пояснить правило одновременной подстановки, сложного заключения, правило силлогизма, контрпозиции и снятия двойного отрицания.
10. Определение формулы, выводимой из совокупности  .
.
11. Привести понятие вывода.
12. Привести основные правила выводимости.
13. Теорема дедукции и обобщенная теорема дедукции.
14. Привести правило введения конъюнкции и дизъюнкции.
15. Сформулировать правило перестановки, соединения и разъединения посылок. Правило исключения третьего.
16. Привести формулировку трех теорем, устанавливающих связь между основными положениями алгебры высказываний и исчисления высказываний.
1. Лихтарников, Л. М. Математическая логика: курс лекций / Л. М. Лихтарников, Т. Г. Сукачева. – СПб.: Лань, 1998.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 77; Нарушение авторских прав?; Мы поможем в написании вашей работы!