Кванторные операции

Из вышесказанного следует, что для превращения одноместного предиката в высказывание нужно подставить вместо его переменной какой-нибудь конкретный предмет из области задания предиката. Такое высказывание называется единичным.

Помимо указанной процедуры образования единичных высказываний в логике предикатов имеются еще две операции, которые превращают одноместный предикат в высказывание. Это применение к предикату операций связывания квантором всеобщности или квантором существования. Каждая такая операция ставит в соответствие одноместному предикату некоторое высказывание, истинное или ложное в зависимости от исходного предиката. Кванторные операции можно рассматривать как обобщение операций конъюнкции и дизъюнкции в случае бесконечных областей.

Квантор (от лат. quantum – сколько), логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа " все ", " каждый ", " некоторый ", " существуе т", " имеется ", " любой ", " всякий ", " единственный ", " несколько ", " бесконечно много ", " конечное число ", а также все количественные числительные. В формализованных языках, составной частью которых является исчисление предикатов, для выражения всех подобных характеристик оказывается достаточным использование двух вышеуказанных кванторов.

1. Квантор всеобщности .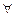

Операция связывания квантором всеобщности 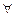– это операция, по которой каждому одноместному предикату , определенному на множестве , сопоставляется высказывание 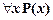, которое истинно, если истинно для каждого элемента , и ложное в противном случае. Это высказывание уже не зависит от . Соответствующее ему словесное выражение записывается так «Для всякого истинно».

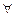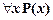Операция связывания квантором всеобщности обозначается символом (происходит от первой буквы англ. Аll – «все»). Сам символ называют квантором общности по переменной . Переменная в предикате называется свободной переменной ( любое из ), а в высказывании переменную называют связанной переменной. Высказывание 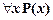называется универсальным высказыванием для предиката .

2. Квантор существования .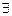

Операция связывания квантором существования 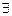– это операция, по которой каждому одноместному предикату , определенному на множестве , сопоставляется высказывание , которое истинно, если истинно для каждого элемента , и ложное в противном случае. Это высказывание уже не зависит от . Соответствующее ему словесное выражение записывается так: «Существует , при котором истинно».

Операция связывания квантором всеобщности обозначается символом 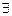(происходит от первой буквы англ. Exist – «существовать»). Сам символ 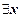называют квантором существования по переменной . Переменная в предикате называется свободной переменной ( любое из ), а в высказывании переменную называют связанной переменной. Высказывание называется экзистенциональным высказыванием для предиката .

Дата добавления: 2017-02-01