Производные правила вывода

Решение

Пример 8.3

Решение

Пример 8.2

Определение доказуемой формулы

Правило заключения.

Если формулы и доказуемы в исчислении высказываний, то формула также доказуема.

Схематическая запись этого правила имеет вид:

├А; ├ А→В.

├В

а) Всякая аксиома является доказуемой формулой.

б) Формула, полученная из доказуемой формулы путем применения подстановки вместо переменной произвольной формулы , есть доказуемая формула.

в) Формула 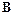, полученная из доказуемых формул и путем применения правила заключения, есть доказуемая формула.

г) Никакая другая формула исчисления высказываний не считается доказуемой.

Процесс получения доказуемых формул называется доказательством.

Примеры доказательств (получения доказуемых формул)

Доказать, что ├ (рефлексивность импликации).

1) Воспользуемся аксиомой I₂:

и выполним подстановку . Тогда получим

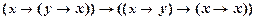├ (8.2.1)

2) В данной формуле можно выделить две части, обозначив их буквами 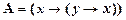и : и , и тогда формулу (8.2.1) можно записать в виде . После этого можно применить правило заключения к аксиоме I₂ и полученной формуле

.

├ ;├

├

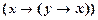В результате получим доказуемую формулу

├ . (8.2.2)

3) В формуле (8.2.2) осуществим подстановку

.

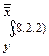В результате получим еще одну доказуемую формулу

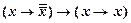├ . (8.2.3)

4) На основании аксиомы IV₂ в составе формулы (8.2.3) имеем доказуемую формулу 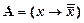и пока еще недоказуемую формулу .

Применим правило заключения к аксиоме IV₂ и формуле (8.2.3).

.

├ ; ├ ,

├

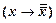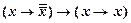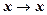
Получим доказуемую формулу

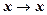├ . (8.2.4)

5) Осуществив подстановку в формуле (8.4) вместо формулу , получим

├ .

Доказать, что ├ .

Интерпретацией доказуемости данной формулы в алгебре логики является закон де Моргана .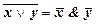

1) Возьмем аксиому II₃ и выполним в ней последовательно две подстановки, заменяя сначала на , а затем на . В результате получим доказуемую формулу

├ . (8.3.1)

2) В формуле (8.3.1) выполним подстановку , получим

. (8.3.2)

Докажем теперь, что формулы

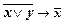(8.3.3)

и 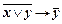(8.3.4)

доказуемы.

3) Возьмем аксиому IV₁ 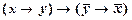и выполним подстановку 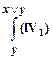, получим доказуемую формулу

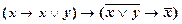├ . (8.3.5)

Левая часть в скобках в формуле (8.3.5) представляет собой аксиому III₁ 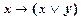, то есть ├ и . Применяя правило заключения, получим

.

├ ; ├ ,

├

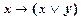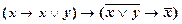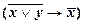
Таким образом, формула (8.3.3) доказана.

4) Для доказательства формулы (8.3.4) опять воспользуемся аксиомой IV₁ и произведем в ней последовательно подстановку на 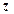, получим ├ 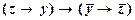, затем на 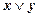: ├ 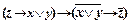и, наконец, 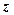на : ├ .

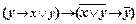В данной формуле в левой части получим аксиому III₂: 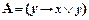, и .

Применяя правило заключения

.

├ ; ├ ,

├

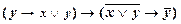получим доказуемую формулу (8.3.4).

5) Теперь применим правило заключения к формулам (8.3.2) и (8.3.3)

├ ; ├

├

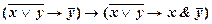
и получим доказуемую формулу

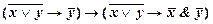├ . (8.3.6)

Применяя правило заключения к формулам (8.3.4) и (8.3.6), получим

.

├ ; ├

├

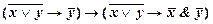
то есть формула доказана.

Производные правила вывода, как и рассмотренные ранее правила подстановки и заключения, дают возможность получать новые доказуемые формулы. Они также получаются с помощью правил подстановки и заключения и поэтому являются производными от них.

Дата добавления: 2017-02-01