Машины Тьюринга

Классификация алгоритмических моделей

Пример 10.3

Пример 10.2

Пример 10.1

Наиболее простой пример бесконечного алгоритмического процесса можно привести из процедуры деления десятичных дробей. Так, числа 11,5 и 5 являются в этом случае допустимыми начальными данными, применение к которым алгоритма деления приводит к искомому результату – 2,3.

Но все будет по-другому для чисел 40 и 6, которые также являются допустимыми начальными данными. Для них алгоритм деления будет выглядеть следующим образом:

40 6

¯ 36 6,66…

¯ 36

…

Данный процесс не встречает препятствий и никогда не заканчивается, так что получить точный результат для чисел 40 и 6 невозможно. Необходимо отметить, что обрыв процесса произвольным образом в данном алгоритме не предусмотрен. Хотя его можно было бы предусмотреть в вычислительном алгоритме при достижении результата заданной точности – количества знаков после запятой.

Теперь приведем пример алгоритма, заходящего в тупик, безрезультатно обрывающегося. Его предписания таковы.

1. Исходное число умножить на 2. Перейти к выполнению п.2.

2. К полученному числу прибавить 1. Перейти к выполнению п.3.

3. Определить остаток от деления полученной в п.2 суммы на 3. Перейти к выполнению п. 4.

4. Разделить исходное число на остаток. Частное является искомым результатом. Конец.

Пусть натуральные целые положительные числа будут допустимыми исходными (начальными) данными для этого алгоритма. Для числа 6 алгоритмический процесс будет проходить так:

1-й шаг: 6 · 2 = 12; переходим к п. 2;

2-й шаг: 12 + 1 = 13; переходим к п. 3.

3-й шаг: остаток (13: 3) = 1, переходим к п. 4.

4-й шаг: 6: 1 = 6. Конец.

Искомый результат равен 6.

Иначе будет протекать алгоритмический процесс для исходного данного 7:

1-й шаг: 7 · 2 = 14; переходим к п. 2;

2-й шаг: 14 + 1 = 15; переходим к п. 3.

3-й шаг: остаток (15: 3) = 0, переходим к п. 4.

4-й шаг: 7: 0 - деление невозможно. Процесс зашел в тупик, натолкнулся на препятствие и безрезультатно оборвался. Конец.

В результате рассмотренных выше особенностей алгоритма можно дать еще одно определение.

Алгоритм – четкая система инструкций, определяющая дискретный детерминированный процесс, ведущий от варьируемых исходных данных (входов) к искомому результату (выходу), если он существует, через конечное число элементарных шагов (тактов) работы алгоритма.

Пожалуй, это будет наиболее полное и точное определение из рассмотренных нами понятий алгоритма.

Алгоритмы, в которых основную роль играют математические действия, называются численными алгоритмами. Но кроме них существуют логические алгоритмы, которые используются в теории игр.

В качестве примера, дающего логический алгоритм, рассмотрим следующую игру.

Имеется 15 предметов. В игре участвуют двое: начинающий и противник. Каждый игрок по очереди берет один, два или три предмета. Выигрывает тот, кто берет последний предмет. Какой стратегии в игре должен придерживаться начинающий, чтобы выиграть?

Выигрышная стратегия начинающего может быть описана в форме следующей таблицы:

Таблица 10.1

Таблица выигрышной стратегии начинающего игрока

Номер хода	Ход начинающего	Ход противника
	4 -
	4 -
	4 -

Почему такая стратегия выигрышная? Потому что в результате предложенной стратегии начинающий возьмет в итоге предметов, а противник – , то есть в сумме они возьмут 15 предметов, и последний предмет будет взят начинающим (у противника в таблице последний ход равен нулю).

Существуют три основных класса универсальных алгоритмических моделей, отличающихся исходными предпосылками относительно того, что такое алгоритм.

Первый класс моделей. Наиболее известная модель данного класса – это машина Тьюринга. Такие модели основаны на представлении об алгоритме как о некотором простейшем детерминированном устройстве для его реализации.

Второй класс моделей. К ним относятся рекурсивные функции, при использовании которых основной упор делается на результат выполнения алгоритма, то есть алгоритм рассматривается с точки зрения его результата.

Третий класс моделей. К этому классу относятся модели, в которых происходит преобразование слов в произвольных алфавитах. В них алгоритм рассматривается как процесс преобразования исходных данных в конечный результат. Классическим примером моделей этого типа являются нормальные алгоритмы Маркова.

Кроме названных моделей известны и другие.

Различие и многообразие типов алгоритмических моделей позволяет выбрать аппарат, наиболее подходящий для целей проводимого исследования. При этом не происходит потери общности формализации благодаря тому, что модели взаимно сводимы. Поэтому оказалось возможным разработать инвариантную по отношению к моделям систему понятий, позволяющую рассматривать и исследовать свойства алгоритмов независимо от того, какая формализация алгоритма выбрана.

Приведенная классификация моделей является традиционной и отражает подходы к их разработке в разное время различными авторами, чьими именами и названы многие алгоритмические модели. В дальнейшем в рамках конструктивной математики были получены результаты, благодаря которым можно рассматривать все модели с единых позиций и не различать машины Тьюринга, рекурсивные функции, нормальные алгоритмы Маркова и т.д.

Введение понятия машины Тьюринга явилось одной из первых и успешных попыток дать точный формализованный математический эквивалент для общего интуитивного представления об алгоритме. Это понятие названо по имени английского математика Алана Тьюринга, сформулировавшего его в 1937 г., за 9 лет до появления первой электронной вычислительной машины.

Определение машины Тьюринга. Машина Тьюринга хоть и названа машиной, но на самом деле является не физической машиной, а математической воображаемой. Она является таким же математическим объектом, как функция, производная, интеграл, группа и т.д. И так же, как и другие математические понятия, машина Тьюринга отражает объективную реальность, моделирует некие реальные процессы.

Тьюринг предпринял попытку смоделировать действия математика (или другого человека), осуществляющего некую умственную деятельность. Такой человек, находясь в определенном «умонастроении» или «состоянии», просматривает некоторый текст, затем вносит в него какие-то изменения, проникается новым «умонастроением» и переходит к просмотру последующих записей.

Машина Тьюринга действует примерно так же. Ее удобно представлять в виде автоматически работающего устройства. В каждый дискретный момент времени устройство, находясь в некотором состоянии, обозревает содержимое одной ячейки, протягиваемой через устройство ленты, и делает шаг, заключающийся в том, что устройство переходит в новое состояние, изменяет (или оставляет без изменения) содержимое обозреваемой ячейки и переходит к обозрению следующей ячейки – справа или слева. Причем шаг осуществляется на основании предписанной команды. Совокупность всех команд представляет собой программу машины Тьюринга.

Опишем машину Тьюринга более подробно. Устройство этой математической воображаемой машины включает в себя:

1. Внешний алфавит – конечное множество знаков, символов, букв , которыми кодируется информация, подаваемая в машину. Машина перерабатывает информацию, поданную в виде слова, в новое слово.

2. Внутренний алфавит – конечное множество знаков, символов, букв 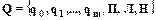, которыми кодируются состояния и действия машины. Символы выражают конечное число состояний машины. Для любой машины число состояний фиксировано. Два состояния имеют особое значение: - начальное состояние машины, - заключительное состояние машины. Находясь в состоянии , машина начинает работать, а попав в состояние , машина останавливается. Символы - это символы сдвига (вправо, влево, на месте).

3. Внешняя память – бесконечная лента в обе стороны, разбитая на клетки, в каждую клетку которой может быть записана только одна буква. Пустую клетку обозначаем символом .

4. Управляющая головка – считывающая головка. Она передвигается вдоль ленты и может останавливаться напротив какой-либо клетки, то есть воспринимать символ. В одном такте работы машины управляющая головка может сдвигаться только на одну клетку (вправо, влево) или оставаться на месте. Каждое сведение, хранящееся на ленте, изображается конечным набором символов (букв) внешнего алфавита, отличного от . К началу работы машины на ленту подается начальное сведение (начальная информация). В этом случае управляющая головка, как правило, находится у крайнего левого знака с указанием начального состояния (рис.10.1) (начальная конфигурация). Работа машины складывается из тактов, по ходу которых происходит преобразование начальной информации в промежуточные информации.

В качестве начальной информации на ленту можно подать любую конечную систему знаков внешнего алфавита (любое слово в этом алфавите), расставленную произвольным образом по ячейкам. Слово в алфавите А или алфавите Q – любая последовательность букв соответствующего алфавита.

В зависимости от того, какая была подана начальная информация, возможны два случая.

1. После конечного числа тактов машина останавливается (переходит в стоп-состояние ), и при этом на ленте оказывается изображенной информация В. В этом случае машина применима к начальной информации А и перерабатывает ее в результирующую информацию В.

2. Машина никогда не останавливается (не переходит в стоп-состояние). В этом случае машина не применима к начальной информации А.

В каждом такте работы машина действует по функциональной схеме, которая имеет вид

.

Здесь , - буквы внешнего алфавита; , 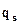- состояния машины; П, Л, Н – символы сдвига.

В зависимости от того, какая буква на ленте обозревается управляющей головкой (в нашей записи ) и в каком состоянии находится машина (в нашей записи ), в данном такте вырабатывается команда, состоящая из трех элементов.

1. Буква внешнего алфавита (), на которую заменяется обозреваемая буква ().

2. Адрес внешней памяти для следующего такта .

3. Следующее состояние машины ().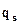

Совокупность всех команд образует программу машины Тьюринга.

Программа представляется в виде двумерной таблицы (двумерной, потому что имеется два алфавита A и Q) и имеет название Тьюринговой функциональной схемы.

Тьюрингова функциональная схема – программа машины Тьюринга, оформленная в виде двумерной таблицы.

Пример такой схемы дан в табл. 10.2 (машина Тьюринга 1).

Ясно, что работа машины Тьюринга полностью определяется ее программой. Иными словами, две машины Тьюринга с общей функциональной схемой неразличимы, и различные машины Тьюринга имеют различные программы.

Таблица 10.2

Тьюрингова функциональная схема

Состояния машины Тьюринга	Последовательность букв внешнего алфавита (слова)

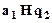
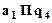
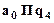
В дальнейшем для простоты изображения различных конфигураций машины Тьюринга будем записывать информацию в виде слова, не изображая ленты и ее разбивки на клетки, и ниже этого слова под соответствующей буквой записывать состояние машины.

Применение машин Тьюринга к словам. Проиллюстрируем примерами работу машины Тьюринга.

Дата добавления: 2017-02-01