Реализующей алгоритм примера 10.7

Решение.

Пример 10.7

Решение

Пример 10.6

Решение

Пример 10.5

Решение

Пример 10.4

Рассмотреть, как работает машина Тьюринга, заданная функциональной схемой (табл.10.2), если начальная конфигурация имеет вид:

.

Так как управляющей головкой обозревается буква 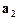, а машина находится в состоянии , то она вырабатывает команду, находящуюся в клетке на пересечении строки и столбца 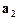, то есть это команда - , при этом управляющая головка перемещается влево, так как в команде стоит буква Л, означающая перемещение головки влево.В результате получится вторая конфигурация

.

Сейчас управляющей головкой снова обозревается буква 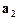, только уже другая, находящаяся на другом месте, при этом машина находится в прежнем состоянии . Понятно, что поскольку и внешняя буква, и состояние машины не изменились, то она снова выработает ту же команду, находящуюся в клетке на пересечении строки и столбца 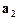, то есть - , при этом управляющая головка снова перемещается влево.В результате получится третья конфигурация

.

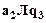Сейчас управляющей головкой обозревается уже другая буква , при этом машина находится в прежнем состоянии . В табл.10.2 на пересечении строки и столбца стоит команда . Следовательно, управляющая головка снова перемещается влево, но там у нас нет обозначенных ячеек, поэтому вводим дополнительную пустую ячейку, которую всегда обозначаем буквой , а прежняя стирается, и вместо нее записывается буква 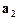, которая является частью вновь выработанной команды. В результате получится четвертая конфигурация

.

Для этой конфигурации машина вырабатывает команду . Видим, что головка перемещается вправо, содержимое ячейки не изменяется, а машина переходит в состояние . Пятая конфигурация будет иметь вид

.

Так как при пятой конфигурации машина находится в состоянии , то машина останавливается, а результатом будет являться слово .

Рассмотреть, как работает машина Тьюринга, заданная функциональной схемой (табл.10.2), если начальная конфигурация имеет вид:

.

Действуя аналогично предыдущему примеру, мы придем к следующим конфигурациям:

- вторая конфигурация,

- третья конфигурация,

- четвертая конфигурация,

- пятая конфигурация,

- шестая конфигурация.

Видно, что вторая и шестая конфигурации повторяются, то есть процесс работы машины начал повторяться и, следовательно, результата не будет.

Тьюринговая функциональная схема 1, заданная таблицей 10.2, может быть записана и в виде строки:

Конструирование машин Тьюринга. Создание (синтез) машин Тьюринга (то есть написание соответствующих программ) является задачей более сложной, чем применение машины к исходным данным (словам).

На примерах рассмотрим, как строятся тьюринговые машины, реализующие некоторые простые арифметические алгоритмы.

Сконструировать машину Тьюринга, реализующую алгоритм перехода от натурального числа к натуральному числу , в десятичной системе счисления. Указать десятичную запись числа , то есть вычислить функцию .

Определим внешний алфавит А. Очевидно, что он должен содержать все цифры от 0 до 9 и символ пустой клетки , то есть . Число будем записывать в десятичной системе на ленте, при этом цифры будут помещаться по одной в каждой клетке подряд без пропусков.

Чтобы решить поставленную задачу, машина должна в первом такте работы стереть последнюю цифру числа , заменить ее цифрой на единицу большей и перейти в стоп-состояние, если последняя цифра была меньше 9. Например, в числе 135 надо последнюю цифру 5 заменить на 6 и остановиться, так задача выполнена.

Если же последняя цифра числа была 9, то машина должна, стерев цифру 9, записать в освободившуюся клетку цифру 0 и произвести сдвиг влево к соседнему разряду (влево, потому что справа цифр нет), оставаясь в том же начальном состоянии. Здесь во втором такте работы машина должна прибавить единицу к цифре более высокого разряда. Например, в числе 139 надо стереть цифру 9, вместо нее на освободившееся место записать 0, перейти влево к цифре 3 и прибавить к ней единицу, получим число 140.

В случае сдвига влево, управляющая головка может выйти на пустую клетку, когда нет цифры более высокого разряда нет. Тогда машина вписывает в пустую клетку цифру 1.

Из сказанного следует, что при реализации алгоритма вычисления функции машина может пребывать лишь в двух состояниях: начальном – и заключительном – .

Тогда машина Тьюринга, реализующая алгоритм перехода от к , в десятичной системе счисления будет иметь вид (табл.10.3):

Таблица 10.3

Программа (схема) работы машины Тьюринга, реализующей алгоритм перехода от натурального числа к натуральному числу , в десятичной системе счисления

Состояния машины Тьюринга	Внешний алфавит

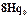
На рис. 10.2, а и б показаны соответствующие конфигурации для чисел 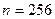и .

а) б)

Рис. 10.2. Результаты обработки чисел (а) и (б) машиной Тьюринга (табл. 10.3), реализующей алгоритм перехода от натурального числа к натуральному числу , в десятичной системе счисления

Сконструировать машину Тьюринга, реализующую алгоритм, по которому из записанных подряд единиц на ленте оставалось бы единицы, также записанные подряд, если при этом 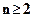и работала бы вечно, если или .

В качестве внешнего алфавита возьмем двухэлементное множество 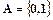. В соответствии с принятыми ранее обозначениями здесь у нас в качестве состояния будет 0, а в качестве состояний станут выступать единицы - 1. Количество необходимых внутренних состояний будет определено в процессе составления программы. Считаем, что машина начинает работать из стандартного начального положения, то есть когда в состоянии обозревается крайняя правая единица из записанных на ленте.

Начнем с того, что сотрем первую единицу, если она имеется, перейдем к обозрению следующей левой ячейки и сотрем там единицу, если она в этой ячейке записана. На каждом таком переходе машина должна переходить в новое внутреннее состояние, иначе в противном случае будут стерты вообще все единицы, записанные подряд.

Если в качестве исходного слова взять

,

то после двух расмотренных шагов машины Тьюринга будем иметь следующую последовательность конфигураций

Команды, осуществляющие описанные действия, при записи в строку будут иметь следующий вид

; .

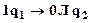Сейчас машина находится в состоянии и обозревает третью справа ячейку из тех, в которых записано данное слово. Не меняя содержимого обозреваемой ячейки, машина должна остановится, чтобы выполнить условие задачи, то есть перейти в заключительное состояние независимо от содержимого ячейки. Вот эта команда для случая, когда третья ячейка справа занята единицей (наш пример)

.

Если же третья ячейка справа занята нулем, то тогда должна выполняться команда

.

Осталось рассмотреть ситуации, когда на ленте записана всего одна единица или не записано ни одной. Если на ленте записана одна единица, например, слово , то после первого шага (выполнив команду 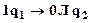) машина будет находиться в состоянии и обозревать вторую справа ячейку, в которой записан 0. По условию задания машина в таком случае должна работать вечно. Это можно обеспечить в частности такой командой

,

выполняя которую шаг за шагом, машина будет двигаться по ленте неограниченно влево (или протягивать ленту через считывающее устройство слева направо).

Наконец, осталось выполнить последнее условие, когда на ленте нет ни одной единицы. В этом случае машина также должна работать вечно. Здесь в начальном состоянии обозревается ячейка с содержимым 0, и вечная работа машины будет обеспечиваться следующей командой:

.

Таким образом, получилось, что число внутренних состояний должно быть равно трем: , , , внешний алфавит, определенный заранее, состоит из двух букв 0 и 1, а также установлены все необходимые действия машины, которые определяются сочетанием букв алфавита и состоянием машины.

Рассмотренный алгоритм можно записать в виде функциональной схемы (табл. 10.4).

Таблица 10.4

Программа (схема) работы машины Тьюринга,

Состояние машины Тьюринга	Последовательность букв внешнего алфавита (слова)

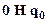
В заключение необходимо отметить, что созданная нами машина Тьюринга может применяться не только к словам в алфавите , представляющим собой записанные подряд единиц при 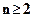. Она применима и ко многим другим словам в этом алфавите, например,: 1011, 10011, 111011, 11011, 1100111, 1001111, 10111, 10110111 и т.д. (исходя из стандартного начального положения у первой единицы справа).

Однако оказывается, что она неприменима к ряду слов, отвечающих условию 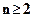, то есть при подаче этих слов она будет работать вечно, вместо того, чтобы остановиться. Например, она неприменима к следующим словам: 101, 1001, 11101, 101101, 1100101101 и т.д.

Рассмотрим работу машины применительно к слову 1001. Конфигурации работы приведены ниже.

; ; ;

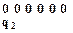
; ; и т.д.

Дата добавления: 2017-02-01