Обработка экспериментальных данных и расчеты

Порядок выполнения работы

1. Записывают спектр поглощения СО в области 2000 - 2250 см^-1 (основной тон). Условия записи: масштаб регистрации – 150мм/см^-1; скорость регистрации – 42 см^-1/мин; щелевая программа – 2.

2. Проводят обработку полученных экспериментальных данных так, как это описано в разделе "Обработка экспериментальных данных и расчеты".

1. На полученном спектре находят и обозначают Р- и R-ветви полосы поглощения.

2. Пронумеровывают все линии вращательной структуры, отсчитывая от центра полосы, где нет поглощения (1,2,3 и т.д. для R-ветви и -1,-2,-3 и т.д. для Р - ветви).

3. Определяют волновое число максимума каждой линии вращательной структуры в Р- и R-ветвях, относят каждую линию к определен­ному переходу между вращательным уровнем нижнего колебательного состояния и вращательным уровнем верхнего колебательного состояния. Данные заносят в табл. 1.5.

Таблица 1.5

Волновые числа вращательных линий колебательно-вращательного спектра поглощения газообразного ______

Р- ветвь	R- ветвь
J	x=-J	, см^-1	, см^-1	J	x=J+1	, см^-1	, см^-1
.	-1 -2 -3

Обозначения: J – вращательное квантовое число нижнего уровня; х – номер линий во вращательной структуре; - волновое число линии в спектре; - разность волновых чисел соседних линий в ветви.

4. Определяют приближенно волновое число основного колебательного перехода по положению нулевой линии, взяв среднее арифметическое значение из волновых чисел двух ближайших к центру полосы линий, одной в Р- ветви, другой – в R-ветви.

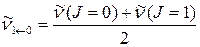
5. Используя приближение модели жёсткого ротатора, рассчитывают величину равновесного межъядерного расстояния.

а) Вычисляют средние величины вращательной постоянной В_е и момента инерции. Для этого определяют среднюю разность волновых чисел между двумя соседними линиями, используя 4 - 5 ближайшие к центру полосы в Р- и R-ветви. Из соотношения находят среднюю величину вращательной постоянной В_е.

б) По уравнениям (1.7) и (1.4) рассчитывают момент инерции I_e и межъядерное расстояние r_e в молекуле.

6. Сопоставляют полученные молекулярные константы B_e, I_e, r_e, а также волновое число основного перехода со справочными данными.

Дополнительные задания

Расчет сумм состояний и распределения молекул по вращательным и колебательным уровням

1. Рассчитывают вращательную сумму состояний Q_r при температуре, указанной преподавателем:

, (1.26)

где фактор симметрии σ = 1.

2. Рассчитывают долю молекул от общего их числа, находящихся на каждом из первых одиннадцати (включая нулевой) вращательных уровнях при температуре, указанной преподавателем.

, (1.27)

где степень вырождения g = 2J+1.

3. Строят график зависимости

4. Рассчитывают колебательную сумму состояний Q_ν при Т = 298 и 1000 К приняв, что волновое число основного тона равно колебательной постоянной: .

, где (1.28)

5. Рассчитывают долю молекул от общего числа, находящихся при 298 и 1000К на нулевом и первом колебательных уровнях. При вычислениях не забывают о том, что Е_кол на нулевом уровне не равна нулю, но энергия колебаний ни любом другом уровне отсчитывается от нулевого. Колебании ядер на нулевом и первом уровнях можно считать гармоническими

(1.29)

Строят график зависимости

Контрольные вопросы к работе 1.3

1. Превращение энергии при поглощении и причина появления полосы поглощения в спектре.

2. Вращательные спектры поглощения двухатомных молекул. Их внешний вид и механизм возникновения. Вращательная энергия и вращательный терм. Вращательная постоянная. Модель “жёсткого ротатора” для определения межъядерных расстояний по вращательным спектрам поглощения. Выражение для собственных значений вращательной энергии.

3. Колебательные спектры поглощения двухатомных молекул. Модель “гармонического осциллятора” для анализа колебательных спектров поглощения. Энергия колебательного движения. Смысл колебательной постоянной. Кривая потенциальной энергии и колебательные уровни. Правило отбора и количество полос в спектре.

4. Основные недостатки модели “гармонического осциллятора”. Модель “ангармонического осциллятора”. Кривая потенциальной энергии и колебательные уровни. Энергия колебательного движения. Правило отбора и вид колебательного спектра.

5. Определение колебательной постоянной, коэффициента ангармоничности, числа колебательных уровней и энергии диссоциации по колебательному спектру поглощения.

6. Колебательно-вращательные спектры поглощения двухатомных молекул. Их вид и природа их возникновения. Определение вращательной постоянной, момента инерции и равновесного межъядерного расстояния по колебательно-вращательному спектру.

Глава. 2. Термохимия

2.1. Термохимические измерения

2.1.1. Тепловые эффекты, теплоёмкость

Для большинства физико-химических расчетов необходимо знать теплоёмкости веществ, тепловые эффекты процессов растворения, фазовых превращений и химических реакций. Эти величины можно измерить экспериментально. При температурах, близких к комнатной, обычно применяют калориметрический метод.

При калориметрических опытах величину и знак теплового эффекта (количества теплоты) Q процесса определяют по изменению температуры Δ t калориметра:

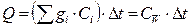, (2.1)

где g_i - массы исследуемого вещества, калориметра и вспомогательных устройств (мешалки, ампулы, термометра); С_i- удельные теплоёмкости исследуемого вещества, калориметра и вспомогательных устройств; С_W - суммарная теплоёмкость системы - это теплоёмкость всех частей системы, участвующих в теплообмене, Дж/К. Уравнение (2.1) может быть записано как:

, (2.2)

где К - константа калориметра, т.е. теплоемкость частей калориметра и вспомогательных устройств, участвующих в теплообмене, Дж/К; C ₁ - теплоёмкость содержимого калориметра; g₁ - масса содержимого калориметра; Δ t - изменение температуры процесса, протекающего в условиях отсутствия теплообмена калориметра с окружающей средой.

Калориметр с изотермической оболочкой позволяет учесть теплообмен егос окружающей средой, что даёт возможность вычислять изменение температурыΔ t, соответствующее опыту без теплообмена.

Теплоёмкость – это мера инертности системы к нагреванию (или охлаждению), она численно равна количеству теплоты, которое необходимо подвести к системе, чтобы повысить её температуру на один градус. Различают среднюю и истинную теплоёмкости. Среднюю теплоёмкость системы в интервале температур Т ₁ – Т ₂ вычисляют по уравнению:

, (2.3)

где Q – количество теплоты, необходимое для повышения температуры системы от Т ₁ до Т ₂.

Истинную теплоёмкость вычисляют по уравнению:

, (2.4)

где С - теплоемкость системы при данной температуре Т. Связь истинной и средней теплоемкостей выражается уравнением:

(2.5)

При ∆ T ≤ 5° даже на совершенных калориметрах (при измерении с точностью 0,05 %) не удаётся установить различия между истинной и средней теплоемкостью. Поэтому теплоемкость, определённую врезультате изменения температуры калориметра до 5º, принимают за истинную.

Теплоемкость системы зависит от её массы, т.е. это экстенсивное свойство системы. Если теплоемкость отнести к единице массы g, то получается интенсивная величина – удельная теплоёмкостьс, Дж/кг×К:

С = с×g или C _ср = с _ср g,

Если же масса равна молярной или атомной массе, то теплоёмкость будет соответственно молярной или атомной С _мол [Дж/(моль×К)].

Если во время опыта давление в калориметрической системе остаётся постоянным (в калориметрах открытого типа оно равно атмосферному), то из определяемого теплового эффекта процесса Q_p по уравнениям (2.3) и (2.4) вычисляют теплоёмкость при постоянном давлении С_р (изобарная теплоёмкость).

Если же во время опыта остается постоянным объем калориметрической системы, а давление изменяется, то из определяемого теплового эффекта процесса Q_v по уравнениям (2.3) и (2.4) вычисляют теплоёмкость при постоянном объеме С_v (изохорная теплоёмкость).

При термохимических измерениях процессам, сопровождающимся выделением теплоты (экзотермическим процессам), приписывается положительный знак, т.е. теплота экзотермического процесса Q > 0, а теплота эндотермического процесса Q < 0.В термодинамической системе знаков все наоборот: положительной считается теплота эндотермических процессов Q_P = D H > 0.

2.1.2. Описание калориметрической установки

Калориметрическая установка состоит из воздушного термостата и помещенного в него калориметра. Термостат представляет собой бокс с застеклёнными дверцами, в котором установлены нагреватель, вентилятор, химический и контактный термометры. Нагреватель выключается при помощи реле при достижении в термостате заданной температуры. В качестве нагревателя воздуха используется электрическая лампочка, обладающая малой тепловой инерцией. Температура в термостате поддерживается с точностью ±0,02°. Воздушная среда в термостате с постоянной температурой является изотермической оболочкой калориметра.

Калориметр представляет собой полиэтиленовый стакан. Через отверстия в крышке бокса в калориметре крепятся стеклянная мешалка, термометр Бекмана, электронагреватель. Калориметр устанавливается в боксе на столике, перемещающемся вертикально. Электронагреватель питается от электросети через стабилизатор и трансформатор. Число оборотов вентилятора и мешалки регулируют лабораторными автотрансформаторами. Напряжение в электронагревателе регулируют реостатом. Отсчеты времени производятся с помощью звукового сигнализатора, подающего сигналы через каждые 30 с.

Тепловой баланс процесса в калориметрической установке выражается уравнением:

Q = ( å g_ic_i)D t¢ + q, (2.6)

Величина q учитывает теплообмен калориметра с окружающей средой за период калориметрического опыта.

Если бы исследуемый процесс и выравнивание температуры в калориметре происходили мгновенно, то теплообмен с окружающей средой отсутствовал (q = 0). В реальных условиях процесс и выравнивание температуры протекают во времени, в течение которого калориметр получает от среды или отдает ей некоторое количество теплоты q. Величину q обычноне вычисляют, а определяют экспериментально. Для этого калориметрический опыт проводят так, чтобы на основании полученных данных можно было бы вычислить изменение температуры D t (отличное от D t¢) того же процесса, но протекающего без тепловых потерь.

2.1.3. Проведение калориметрического опыта

Экспериментследует начинать при условии, когда система близка к состоянию теплового равновесия, характеризуемого постоянным температурным ходом (не более 0,04 град/мин). Это условие можно выполнить, установив температуру содержимого калориметра при работающей мешалке на 1-2° ниже температуры воздуха в боксе. При такой разности температур скорость поступления теплоты в калориметр от воздуха становится равной скорости отдачи теплоты за счёт испарения воды, находящейся в калориметрическом сосуде, что обеспечивает тепловое равновесие системы. При постоянной скорости изменения температуры производят 10-12 измерений по термометру Бекмана через каждые 30 с. Это - начальный период калориметрического опыта. Далее в калориметре осуществляют необходимый эксперимент: растворяют соль, смешивают реагенты, включают нагрев и т.п. При этом температуру по термометру Бекмана продолжают непрерывно записывать через те же промежутки времени. За счёт выделения или поглощения теплоты в процессе происходит резкое изменение температуры. Это - главный период калориметрического опыта. По завершении главного периода вновь устанавливается равномерный ход температуры. Это - конечный период калориметрического опыта, в течение которого производят еще 12 - 15 измерений температуры по термометру Бекмана.

2.1.4. Определение величины Δ t

Величину Δ t с учётом теплообмена обычно рассчитывают графическим способом (рис. 2.1).

Рис. 2.1. Типичный вид температурной кривой калориметрического опыта при экзотермическом процессе в главном периоде

Для этогорезультаты калориметрического опыта представляют графически на миллиметровой бумаге: по оси абсцисс откладывают время в масштабе 1 мин = 1 см, а по оси ординат - температуру, выбор масштаба которой зависит от величины Δ t. Если Δ t ≤ 1º, то выбирают 1º = 10 см,если Δ t ≥ 1º, то принимают 1^о = 5 см. После того, как на график нанесены все экспериментальные точки, получается кривая ABCD. Участок АВ на ней соответствует начальному периоду калориметрического опыта, ВС - главному, а CD - конечному. Чтобы определить изменение температуры Δ t, не искажённое теплообменом, происходящим в течение главного периода, продолжают АВ и CD до пересечения с вертикальной прямой EF. Для этого точки т и п, соответствующие начальной и конечной температурам главного периода, наносят на ось ординат. Через середину отрезка mn проводят линию КР. Пересечение этой линии с кривой ВС даёт точку l, определяющую положение прямой EF. Отрезок EF и будет равен Δ t, отрезок mn = Δ t'. Чем меньше температурный ход в начальном и конечном периодах, тем меньше потери теплоты за счёт теплообмена и тем ближе Δ t' к Δ t.

Для определения тепловых эффектов в калориметрических опытах необходимо знать суммарную теплоёмкость системы C_W. Эту величину рассчитывают из опытных данных по уравнению (2.1), сообщив системе известное количество теплоты Q и определив графически Δ t. Дозированное количество теплоты можно сообщить системе, подведя к ней электрическую энергию или растворив соль с известной теплотой растворения.

2.1.5. Определение суммарной теплоёмкость системы C_W

электрическим методом

Наиболее распространённым методом определения С_W является электрический метод. К калориметрической системе подводят известное количество электрической энергии, превращающейся в теплоту Q. Измеряют силу тока I (A), падение напряжения на нагревателе E (В) и время пропускания тока τ (с). Количество сообщённой системе теплоты вычисляют по закону Джоуля–Ленца:

(2.7)

Изменение температуры Δ t калориметрической системы в ходе этого опыта определяют графически, как это было описано выше (раздел 2.1.4, рис. 2.1).

Последовательность выполнения работы. Включают вентилятор и термостат, установленный на температуру в пределах 24-26 °С. В калориметрический сосуд заливают 200 см³ воды (или исследуемой жидкости). Устанавливают его в термостат и закрепляют на такой высоте, чтобы ртутный резервуар термометра Бекмана был полностью покрыт водой (или исследуемым раствором). Лопасти мешалки должны быть расположены у дна сосуда.

Включают мешалку, устанавливают с помощью реостата предельную скорость вращения, при которой не происходит разбрызгивания исследуемой жидкости. Нагревают до температуры на 1-2º ниже температуры воздуха в боксе, что соответствует ~1º по термометру Бекмана. Проверяют скорость изменения температуры содержимого калориметра, которое не должно превышать 0,04 град./мин. Начинают запись показаний термометра Бекмана с точностью 0,01 град. через 30 с (начальный период). После одиннадцатого отсчёта включают нагреватель на время τ, не прерывая записи показаний термометра Бекмана через каждые 30 с. Температура вначале резко повышается (главный период), затем, после выключения нагревателя, начинает равномерно падать, приближаясь к равновесной температуре калориметра t _равн. Отсчётом температуры, с которой начинается равномерное понижение, кончается главный период калориметрического опыта и начинается конечный период. Производят еще 12 - 15 отсчетов после того, как установится постоянный ход температуры. Выключают мешалку. Определяют графически изменение температуры Δ t (рис. 2.1). Вычисляют суммарную теплоемкость C_w по уравнению:

(2.8)

2.1.6. Определение суммарной теплоёмкости системы C_W по

теплоте растворении КCl

За теплоту Q в этом случае принимают теплоту растворения навески соли (обычно KCl).

Последовательность выполнения работы. В стакан калориметра заливают 200 см³ воды. Взвешивают на весах ~2 г тщательно измельченной соли KCl. Проводят операции, аналогичные описанным в разделе 2.1.3. После начального периода калориметрического опыта (после 11-го измерения температуры по термометру Бекмана) всыпают навеску KCl в калориметр и продолжают запись температуры через каждые 30 с. Температура воды при эндотермическом растворении сначала резко падает (главный период), затем начинает равномерно расти, приближаясь ксредней температуре системы. Отсчётом температуры, с которой начинается её равномерное повышение, кончается главный период калориметрического опыта и начинается конечный период. После него проводят ещё 12-15 измерений температуры (конечный период).

Далее определяют графически изменение температуры Δ t _раств и суммарную теплоемкость системы по уравнению:

, (2.9)

где Q – теплота растворения KCl, Дж/моль; g ₂ – навеска KCl (около 2 г); М ₂ – молярная масса KCl.

Работа 2.1. Определение удельной интегральной теплоты

растворения соли

Цель работы. Определить интегральную теплоту растворения соли Q, предварительно определив суммарную теплоёмкость калориметрической системы электрическим методом (вариант А) или по теплоте растворения хлорида калия (вариант Б).

Теоретическое обоснование. Тепловой эффект, сопровождающий растворение определённого количества вещества в опредёленном количестве растворителя, называют интегральной теплотой растворения. Тепловой эффект, отнесенный к 1 моль растворяемого вещества, называют молярной теплотой растворения, к 1 г – удельной теплотой растворения. Теплота растворения зависит от концентрации раствора.

Дифференциальной теплотой растворения называют тепловой эф­фект, сопровождающий процесс растворения 1 моль вещества в бесконечно большом объёме раствора заданной концентрации (настолько большом объёме раствора, что растворение 1 моль вещества не изменяет его концентрации).

Интегральные теплоты растворения определяют экспериментально, а дифференциальные вычисляют из зависимости интегральных теплот растворения от концентрации раствора:

, (2.10)

где g - навеска исследуемого вещества, г;Δ t _раств - изменение температуры при растворении.

Дата добавления: 2017-02-01