
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Последовательность выполнения работы
|
|
|
|
1. Определяют суммарную теплоёмкость калориметра с водой электрическим методом (раздел 2.1.5). В калориметр наливают 200 см3 (~200 г) воды. С помощью нагревателя доводят в нём температуру до 1º по термометру Бекмана, дожидаются равновесия, когда температурный ход будет не более 0,02º за 30 с и проводят опыт: 10-12 измерений температуры по термометру Бекмана – начальный период, затем пропускают ток I = 2 А через нагреватель в течение t = 2 мин – главный период. Записывают показания вольтметра Е. Конечный период опыта – 10-12 измерений температуры по термометру Бекмана. Графически определяют ∆t главного периода (раздел 2.1.4).
2. Постоянную калориметра К вычисляют из уравнения:
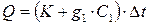 ,
,
где
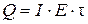 .
.
3. Рассчитывают суммарную теплоёмкость калориметра:
CW = К + С 1 g 1,
где С 1 – удельная теплоёмкость воды; g 1 – навеска воды (200 г).
4. Повторяют опыт. Если значения СW в двух опытах окажутся близкими, то берут их среднее значение.
5. Определяют суммарную теплоёмкость калориметра с раствором соли. Для этого заливают в предварительно взвешенный калориметр 200 см3 раствора соли, взвешивают его вновь и проводят опыт аналогично двум предыдущим.
6. Определяют CW калориметра с раствором по уравнению:
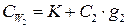
7. Истинную теплоёмкость раствора вычисляют по уравнению:
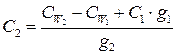
Работа 2.3. Определение средней теплоёмкости веществ
Цель работы. Определить среднюю теплоёмкость вещества, предварительно определив суммарную теплоёмкость калориметра.
Методика проведения опыта. Установка состоит из двух ультратермостатов. В одном из них поддерживает температуру ~25 ºС (холодный термостат). В другом термостате (горячем) поддерживается температура ~50 ºC. В холодном термостате имеется калориметр (стеклянная пробирка объёмом 120 см3), в который помещён термометр Бекмана. В горячем термостате имеется пробирка объёмом 3 см3 для исследуемого вещества и химический термометр.
Последовательность выполнения работы. Работа выполняется в 3 этапа:
1. Определяют суммарную теплоёмкость калориметра по уравнению:
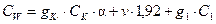 ,
,
где g к, g 1– массы калориметра и воды, соответственно, г; Ск, С 1 – удельные теплоёмкости калориметра и воды; a - часть калориметрического сосуда, заполненная водой; v - объём погруженной части термометра Бекмана
2. Определяют тепловую константу пустой пробирки для вещества, находящейся в горячем термостате:
Взвешивают калориметр на технических весах (gк), заливают в него 50 см3 воды (навеска g 1= 50 г). Включают ультратермостаты. Через 40 мин начинают опыт. Измеряют температуру воды в калориметре по термометру Бекмана через 30 с. После 11-го измерения пустую пробирку из горячего термостата быстро переносят в калориметр с водой, перемешивая воду пробиркой. Сначала наблюдается резкое повышение температуры, затем постепенное её уменьшение.
Делают 11 измерений по термометру Бекмана при равномерном изменении температуры. Затем записывают показания химического термометра в горячем термостате (t 1) и им же замеряют температуру в калориметре (t 2). Определяют графически ∆t (см. раздел 2.1.4). Рассчитывают тепловую константу пробирки по уравнению:
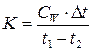
Опыт повторяют ещё раз для уточнения значения К.
3. Определяют среднюю теплоёмкость вещества. Взвешивают пробирку на аналитических весах, заполняют её на 2/3 объёма веществом и вновь взвешивают. Помещают пробирку в горячий термостат и через 40 мин проводят опыт, подобный описанному в п. 2. Среднюю теплоёмкость вещества рассчитывают из уравнения:
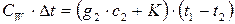 ,
,
где g 2 – навеска вещества, г; с 2– средняя удельная теплоёмкость вещества.
Контрольные вопросы
Общие вопросы для всех работ
- Первое начало термодинамики. Закон Гecca.
- Основы калориметрического метода.
- Особенности конструкции термометра Бекмана.
- Графический метод определения поправки на теплообмен калориметра с окружающей средой.
- Устройство калориметра с изотермической оболочкой.
- Последовательность проведения опыта по определению суммарной теплоёмкости системы электрическим методом.
Вопросы к работе 1
1. Что называют интегральной и дифференциальной теплотами растворения?
2. Последовательность проведения опыта по определению D t раств при растворении соли.
3. Что называют суммарной теплоёмкостью системы?
4. Последовательность проведения опыта по определению CW.
5. Уравнения для расчета суммарной теплоёмкости и удельной интегральной теплоты растворения.
6. Последовательность определения константы калориметра по теплоте растворения КС1.
Вопросы к работам 2 и 3
1. Что называют теплоёмкостью вещества?
2. Связь истинной и средней теплоёмкости.
3. С какой целью определяют суммарную теплоёмкость системы по воде?
4. Уравнение для расчёта истинной теплоёмкости жидкости.
Глава 3. Термодинамика фазовых равновесий
3.1. Основные понятия. Правило фаз
Гетерогенными фазовыми равновесиями называются равновесия, устанавливающиеся в физических процессах перехода веществ из одной фазы в другую. Такие равновесия наблюдаются при кипении жидкости под постоянным давлением (жидкость ↔ пар), плавлении кристаллов (твёрдое тело ↔ жидкость), при выделении кристаллов из насыщенного раствора и в других процессах. Термодинамическое равновесие в гетерогенных системах характеризуется сколь угодно длительным сосуществованием различных фаз в условиях постоянства давления и температуры. При этом концентрации веществ в каждой фазе не изменяются. В целом многофазная гетерогенная система в состоянии истинного равновесия имеет минимальное абсолютное значение энергии Гиббса.
Каждое вещество, которое может быть выделено из системы и существовать вне её, называют составляющим систему веществом. Так, например, в водном растворе хлористого натрия составляющими веществами являются H2O и NaCl, ионы Na+ и Cl– не могут быть причислены к составляющим, хотя и существуют в растворах в виде самостоятельно перемещающихся, кинетически независимых частиц.
Количество каждого из составляющих веществ, входящих в систему, в которой отсутствуют химические реакции, не зависит от количества других веществ. Если же в системе протекают химические реакции, то количества составляющих веществ, входящих в равновесную систему, зависят друг от друга. Состав фаз равновесной системы в этом случае можно определить, зная концентрации лишь части составляющих веществ. Тогда концентрации остальных веществ определяются по уравнению реакции и константе химического равновесия. Вещества, концентрации которых определяют состав фаз данной равновесной системы, называют независимыми составляющими или компонентами системы.
Число компонентов равняется числу составляющих веществ системы минус число уравнений, связывающих концентрации этих веществ в равновесной системе.
Фазой системы называют совокупность всех гомогенных частей системы, имеющих одинаковые физические, химические свойства и отделенных от других частей системы видимыми границами (поверхностью) раздела. Так, например, в системе, состоящей из тающего льда, все куски льда образуют одну фазу, а вода – другую фазу.
Условием равновесия в гетерогенной системе является равенство во всех фазах температуры, давления и химических потенциалов каждого компонента. Между числом компонентов и количеством фаз в равновесной системе существует связь, установленная правилом фаз. Если на состояние системы оказывают влияние такие независимые параметры, как давление и температура, то максимальное число фаз Ф, которое может существовать в системе, содержащей К компонентов, равно Ф = К + 2. В этом случае система находится в равновесии при строго определенных значениях давления и температуры.
Если же Ф < К + 2, то для существования равновесия в системе возможны некоторые вариации значений параметров и концентраций составляющих системы. Это число вариаций называют числом термодинамических степеней свободы f. Число f определяет число независимых параметров, которые можно изменять в известных пределах без изменения числа и природы фаз в равновесной гетерогенной системе и рассчитывается по уравнению:
f = К – Ф + 2(3.1)
Уравнение (3.1) представляет собой математическое выражение правила фаз, выведенного Гиббсом в 1876 г. Оно описывает общие закономерности, которым подчиняются равновесные гетерогенные системы, состоящие из любого числа фаз и любого числа компонентов. На основании правила фаз Гиббса проводят классификацию систем:
· по числу компонентов: одно-, двух- или трёхкомпонентные системы;
· по числу фаз: одно-, двух- или трёхфазные системы;
· по числу степеней свободы: нонвариантная, моновариантная и бивариантная системы.
В дальнейшем будем рассматривать системы в порядке увеличения числа компонентов в них.
Физико-химический анализ. Взаимосвязь физических и химических явлений выражается прежде всего в том, что любое изменение химического состава системы сразу влияет на изменение её физических свойств. На этом основан метод физико-химического анализа, предложенный в конце ХIХ в Н. С. Курнаковым. Суть метода заключается в изучении зависимости различных физических свойств системы от её химического состава и выражении результатов в графической форме – в виде диаграмм состав - свойство, называемых диаграммами состояния. В качестве физических свойств часто используется:
· в термодинамике – давление и температура;
· в электрохимии – электропроводность, ЭДС;
· в спектрохимии – оптическая плотность, рефракция, поляризация;
· в металловедении – твердость, прочность и т.д.
Физико-химический анализ основан на двух принципах:
Принцип непрерывности. При непрерывном изменении параметров, определяющих состояние системы, свойства отдельных её фаз изменяются непрерывно; при этом свойства системы в целом изменяются тоже непрерывно, но при условии, что не возникают новые фазы и не исчезают имеющиеся. Так, например, температура при охлаждении раствора уменьшается непрерывно (плавно) до тех пор, пока раствор не станет насыщенным и не начнут выпадать кристаллы одного из компонентов. Появление второй фазы будет отмечено как излом на кривой охлаждения (зависимость температуры системы от времени охлаждения). Построив график по результатам измерений на растворах с известными концентрациями, можно использовать его для анализа состава неизвестного раствора.
Принцип соответствия. Каждой совокупности фаз, находящихся в данной системе в равновесии, соответствует на диаграмме состояния определённый геометрический образ.
3.2. Фазовые равновесия в однокомпонентных системах
В случае однокомпонентных систем в уравнение состояния входят три переменные: температура, давление и объём. Для графического изображения соотношения между T, p и V однокомпонентной системы необходимо использовать объёмную трёхкоординатную диаграмму. В большинстве случаев для удобства анализа в качестве независимых переменных принимают температуру и давление. Беря сечение объёмной диаграммы при V = const, получают двумерную (плоскую) диаграмму (рис. 3.1). Каждая точка на диаграмме представляет сочетание температуры и давления, при которых находится система. Это позволяет разбить плоскость диаграммы на три области, отвечающие равновесному существованию определённой фазы (твёрдой, жидкой или газообразной).
Точки, отражающие состояние и условия существования системы, называют фигуративными точками. Согласно принципу соответствия физико-химического анализа фигуративныеточки, лежащие внутри областей, отвечают равновесному существованию одной фазы. Например, точка 1 соответствует устойчивому состоянию твердой фазы. Применив правило фаз (3.1), получим, что в этой точке (и во всей области) К = 1, Ф = 1 (твёрдая фаза) и, следовательно, f = 2(можно изменять и температуру, и давление, не выходя за границы этой области). При изобарном нагревании система достигает точки 2, лежащей на кривой плавления. Каждая точка на этой линии отвечает совместному существованию двух фаз – твёрдой и жидкой.
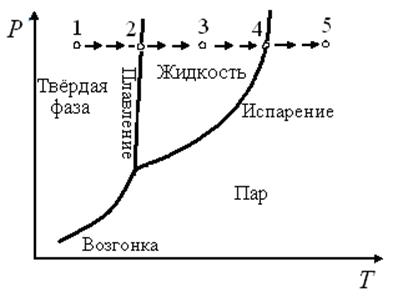
Рис. 3.1. Диаграмма состояния однокомпонентной системы в координатах давление – температура
Появление второй фазы уменьшает число степеней свободы на единицу, f = 1. В точке 2 (и для всех точек на кривой плавления) для сохранения равновесия двух фаз произвольно можно изменять только один параметр, ибо второй параметр связан с уравнением Клапейрона:
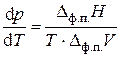 , (3.2)
, (3.2)
где Δф.п. H – теплота фазового перехода, Δф.п. V – изменение объёма при фазовом переходе. Это уравнение описывает взаимосвязь давления и температуры для всех агрегатных превращений (плавления, испарения или возгонки).
При дальнейшем повышении температуры твердая фаза исчезает, остается одна жидкая. Применив правило фаз для точки 3, получим аналогично точке 1 f = 2 (можно изменять и температуру и давление). Нагревая жидкость до температуры точки 4, получаем вторую фазу – насыщенный пар. Насыщенным паром называют пар, находящийся в равновесии с жидкостью. Температурой кипения называют температуру, при которой давление насыщенного пара равно внешнему давлению. Нормальная температура кипения (н.т.к.) – температура кипения при давлении 760 мм рт. ст (1 атм).
Для удобства интегрирования уравнения (3.2) в случае испарения (или возгонки) принимают следующие допущения:
· Теплота испарения не зависит от температуры: Δисп Н .= const.
· Объем пара много больше объема жидкости: V п >> V ж, тогда
Δисп V = V п - V ж » V п
· Пар подчиняется уравнению состояния идеальных газов pV = RT
C учетом сделанных допущений уравнение (3.2) принимает вид
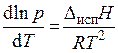 , (3.3)
, (3.3)
а после интегрирования
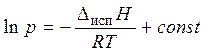 , или
, или 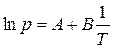 , (3.4)
, (3.4)
где А = const, 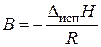 .
.
Зависимость (3.4) в координатах 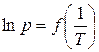 представляет прямую линию, по наклону которой можно определить Δисп Н (Δисп Н = − R · B).
представляет прямую линию, по наклону которой можно определить Δисп Н (Δисп Н = − R · B).
Интегрирование уравнения (3.3) в пределах от Т 1 до Т 2 дает:
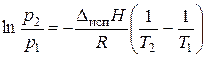 (3.5)
(3.5)
Используя (3.5), можно рассчитать теплоту испарения Δисп Н по двум значениям давления и температуры.
Сделанные допущения не вносят в расчеты больших погрешностей при температурах, далеких от критической Т кр. Однако по мере приближения к Т кр теплота испарения Δисп Н и изменение объёма Δисп V стремятся к нулю, а пар уже нельзя считать идеальным газом.
Зная теплоту испарения, можно вычислить энтропию испарения при температуре Т по уравнению:
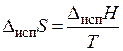 (3.6)
(3.6)
Работа 3.1. Определение давления насыщенного пара
динамическим методом
Цель работы. Получить зависимость давления насыщенного пара воды (или другой жидкости) от температуры динамическим методом.
Последовательность выполнения работы. Динамический метод основан на определении температур кипения жидкости при различных давлениях. Схема установки представлена на рис. 3.2.
В сосуд 3 помещают примерно 100 см3 исследуемой жидкости и закрывают пришлифованной пробкой с термометром 4. Сосуд соединяют с электрическим вакуумным насосом 12 через холодильник 7, в котором конденсируются пары исследуемой жидкости и возвращаются в сосуд 3. Это необходимо для предупреждения попадания жидкости в измерительную систему ртутного вакуумметра 10 и вакуумный насос. Кран 8 служит для соединения вакуумной системы с атмосферой. Сосуд с исследуемой жидкостью снабжён водяной рубашкой, соединенной с термостатом 1.
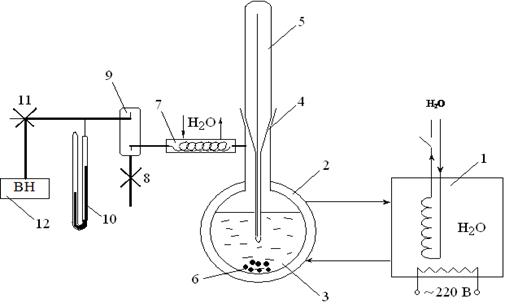
Рис. 3.2. Схема экспериментальной установки:
1 – термостат; 2 – водяная рубашка; 3 – сосуд с исследуемой жидкостью; 4 – шлиф; 5 –- термометр на шлифе 6 – стеклянные капилляры с запаянным концом; 7 – холодильник; 8 – вакуумный кран; 9 – отбойник; 10 – ртутный вакуумметр; 11 – трёхходовой кран; 12 – вакуумный насос
Первое измерение проводят при комнатной температуре. Для этого устанавливают краны 8 и 11 в положение, закрытое от атмосферы. Включают в сеть вакуумный насос 12 и внимательно следят за поведением исследуемой жидкости. Появление первых пузырьков пара в объеме жидкости свидетельствует о том, что давление насыщенного пара жидкости при комнатной температуре стало равным давлению в установке. В этот момент трехходовой кран 11 следует повернуть так, чтобы отключить вакуумный насос от измерительной системы и соединить его с атмосферой.
Нельзя допускать бурного кипения жидкости, поскольку в этом случае система будет очень далека от равновесия. Через 5 мин записывают показания термометра 4 и разность столбов ртути h в вакуумметре 10.
Для перехода к другой температуре прежде всего приводят давление в установке к атмосферному. С этой целью осторожно приоткрывают вакуумный кран 8 и медленно впускают воздух (при быстром впускании воздуха в измерительную часть установки ртуть может разбить запаянное колено вакуумметра 10 и разлиться). После этого при помощи термостата 1 повышают температуру в сосуде 3 на 4-6 оС и вновь проводят аналогичные измерения температуры и давления. Следует выполнить 8-10 таких измерений, каждый раз повышая температуру на 4-6 оС. Результаты записывают в табл. 3.1.
Таблица 3.1
| t, oC | Т, К | 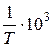 , К-1 , К-1
| p, мм рт. cт. | ln p |
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 103; Нарушение авторских прав?; Мы поможем в написании вашей работы!