Энергии Гиббса образования раствора

1. Выписывают из справочника [2] (табл. 20, с. 26) данные о парциальных давлениях компонентов раствора в зависимости от концентрации.

2. Рассчитывают активности a_i компонентов по отношению давлений и коэффициенты активности γ _i компонентов при всех концентрациях.

3. Рассчитывают относительные химические потенциалы компонентов в данном и идеальном растворах:

Δμ _{i ,реал.} =RT· ln a_i;

Δμ _{i, идеал.} =RT· ln X_i.

4. Рассчитывают энергию Гиббса образования 1 моля раствора:

G^М = X ₁Δμ₁ + X ₂Δμ₂

5. Строят графики в координатах G^М _реал - X ₂ и G^М _идеал - X ₂ на одном листе миллиметровки, а графики γ₁ - X ₂ и γ₂ - X ₂ - на другом.

6. Исходные данные и результаты вычислений заносят в табл. 3.7.

Таблица 3.7

Концентрация	pi	ai	g i	Δμ i	G^M

По результатам проведенных расчетов делают вывод о характере и причинах отклонений данного раствора от закона Рауля.

Контрольные вопросы

1. Что называют парциальной мольной величиной?

2. В чём заключается метод касательной для определения парциальной мольной величины?

3. В чём заключается метод пересечений для определения парциальной мольной величины?

4. В чём смысл уравнения Гиббса–Дюгема?

5. Напишите выражения для химического потенциала компонента в идеальном и реальном растворах.

6. Что называют активностью компонента в растворе?

3.3.2. Равновесие жидкость–пар в двухкомпонентных

жидких системах

При смешении двух жидкостей могут наблюдаться всевозможные степени взаимной растворимости: от практически полной нерастворимости друг в друге (ртуть – вода) до смешения в любых соотношениях с образованием однофазной системы – раствора (этанол – вода).

Раствор называют идеальным (совершенным), если он подчиняется закону Рауля при всех концентрациях. Из закона Рауля (3.7) следует, что парциальные давления паров компонентов (А и В) над раствором являются линейной функцией мольной доли. Растворы подчиняются закону Рауля, если силы взаимодействия между разноименными частицами f_A-B, равны силам взаимодействия между одноименными частицами f_A-A и f_B-B. При этом смешение компонентов не сопровождается ни поглощением, ни выделением теплоты (Δ_см H = 0), ни изменением объёма (Δ_см V = 0).

По отклонению свойств раствора от свойств идеальных растворов можно судить о силах взаимодействия между молекулами его компонентов. Если силы взаимодействия между разноименными частицами меньше сил взаимодействия между одноименными частицами f_A-В < f_A-A и f_A-В < f_B-B, то при смешении таких компонентов происходит поглощение теплоты (Δ_см H > 0) и увеличение объёма (Δ_см V > 0). Это уменьшает теплоту парообразования и, следовательно, повышает давление пара по сравнению с рассчитанным по закону Рауля. При образовании таких растворов наблюдаются положительные отклонения от закона Рауля (рис. 3.7а).

Если силы взаимодействия между разноименными частицами больше сил взаимодействия между одноименными частицами, f_A-В > f_A-A и f_A-В > f_B-B, то при смешении таких компонентов происходит выделение теплоты (Δ_см H < 0) и уменьшение объёма (Δ_см V < 0). Это повышает теплоту парообразования и, следовательно, уменьшает давление пара по сравнению с рассчитанным по закону Рауля. При образовании таких растворов наблюдаются отрицательные отклонения от закона Рауля (рис. 3.7б).

Рис. 3.7. Положительные (а) и отрицательные отклонения (б) от закона Рауля

Из практики известно, что состав пара по сравнению с составом жидкости обогащен легколетучим компонентом. Это положение постулирует первый закон Коновалова: пар по сравнению с находящейся с ним в равновесии жидкостью относительно богаче тем компонентом, добавление которого к системе повышает общее давление пара, т.е. понижает температуру кипения смеси.

Первый закон Коновалова имеет большое практическое значение для разделения жидких смесей кипячением, поскольку при перегонке пар постепенно обогащается более летучим компонентом.

Если отклонения от закона Рауля очень велики, зависимость общего давления от состава раствора может иметь максимум (в случае положительных отклонений) или минимум (в случае отрицательных отклонений). Экстремальные зависимости описывает второй закон Коновалова: в точках экстремума давления пара (или температуры кипения) составы пара и жидкости совпадают.

Смеси, составы которых соответствуют точкам экстремума, кипят как однокомпонентные системы. Такие смеси Коновалов назвал азеотропными, что в переводе означает нераздельнокипящие.

Вместо диаграмм давление пара – состав при постоянной температуре (рис. 3.8а) удобнее использовать диаграммы температура кипения – состав при постоянном давлении (рис. 3.8б). Такие диаграммы часто называют диаграммами кипения.

Рис. 3.8. Диаграммы равновесия жидкость – пар в координатах:

а – давление – состав пара (жидкости), б – температура – состав пара (жидкости)

Так как компонент А с более высоким давлением пара кипит при более низкой температуре , то диаграмма Т _кип – Х имеет зеркально-подобный вид по отношению к диаграмме Р – Х (имеется только качественное подобие).

Нижняя линия на рис. 3.8б носит название кривой жидкости (или кривой кипения). Она представляет собой зависимость температуры начала кипения (конца конденсации) от состава смеси. Это означает, что поле диаграммы ниже кривой жидкости соответствует равновесному состоянию жидкой фазы.

Верхняя линия на рис. 3.8б носит название кривой пара (или кривой конденсации). Она представляет собой зависимость температуры концакипения (начала конденсации) от состава смеси. Это означает, что поле диаграммы выше кривой пара соответствует равновесному состоянию паровой фазы.

Между кривыми жидкости и пара находится гетерогенная область, которая отвечает равновесию двух фаз: жидкости и пара. Любая точка, называемая фигуративной (например, точка o на рис. 3.8б), в этой области описывает лишь общий (брутто) состав смеси. Для нахождения составов равновесных фаз через эту точку необходимо провести конноду - горизонтальную линию, соединяющую точки составов равновесных фаз. На рис. 3.8б коннодой будет служить изотерма аb. Пересечение конноды с кривой жидкости (точка b) определяет состав жидкой фазы, а пересечение с кривой пара (точка a) – состав паровой фазы.

При расчётах фазовых равновесий необходимо определять количество компонентов в каждой из равновесных фаз при заданном общем составе. Для этого используется правило рычага: о тношение равновесных количеств пара и жидкости обратно пропорционально отношению отрезков, на которые фигуративная точка системы делит конноду. Для диаграммы на рис. 3.8б правило рычага записывается так:

Процесс нагревания двухкомпонентной жидкой смеси иллюстрирован стрелками на рис. 3.8б. При нагревании исходной смеси Х ₀ до температуры начала кипения Т _н.к. первые порции пара имеют состав . Согласно первому закону Коновалова состав пара обогащён более летучим компонентом А. Соответственно жидкость будет обогащаться более высококипящим компонентом В. При дальнейшем нагревании с повышением температуры состав пара будет изменяться по кривой пара, а состав жидкости – по кривой жидкости. Когда вся жидкая смесь испарится, состав пара будет равен составу исходной смеси. Состав последних капель жидкости отвечает точке .

Работа 3.4. Построение диаграммы кипения для двухкомпонентных жидких смесей

Цель работы. Построить диаграмму кипения бинарной системы.

Методика выполнения работы. Для определения температур кипения жидкостей служит прибор эбуллиоскоп, который изображен на рис. 3.9.

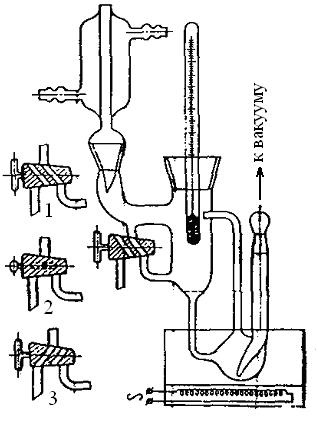
Рис. 3.9. Эбуллиоскоп Свентославского для изучения равновесия жидкость – пар в двойных системах

Исследуемый раствор заливают через воронку, вставленную в обратный холодильник, на 2/3 объёма сосуда для кипячения. Подают воду в обратный холодильник и медленно нагревают сосуд с раствором. Когда раствор закипит, следует внимательно следить за показаниями термометра. Если образующийся пар конденсируется в обратном холодильнике, а конденсат при положении крана 1 возвращается в колбу для кипячения, то состав кипящей жидкости остается постоянным. В этом случае температура кипения тоже остается постоянной. Следует выдержать систему при нагревании 2 - 3 мин, чтобы удостовериться в постоянстве температуры кипения (состоянии равновесия системы кипящая жидкость – пар).

Далее переводят двухходовой кран в положение 2 и собирают в углублении над краном 3 - 5 капель конденсата. После чего переводят кран в положение 3 и отбирают пробу конденсата в колбу с притертой пробкой. Анализ состава конденсата проводят по калибровочному графику показатель преломления – состав смеси.

После отбора пробы кран возвращают в положение 1 и продолжают кипятить раствор для определения температуры кипения после отбора пробы, которая не должна отличаться от температуры кипения до отбора пробы более чем на 1⁰.

Последовательность выполнения работы

1. В восьми конических колбах с притертыми пробками приготавливают бинарные растворы по 10 см³ каждый с различным объемным содержанием компонентов (по указанию преподавателя).

2. На рефрактометре измеряют показатели преломления приготовленных растворов и чистых жидкостей, далее строят калибровочную кривую (зависимость показателя преломления от состава). Порядок работы на рефрактометре описан в приложении 1.

3. Заливают в эбуллиоскоп первую приготовленную смесь, доводят до кипения и определяют её температуру кипения.

4. Отбирают для анализа небольшое количество конденсата так, как это было описано выше. Пробирку с конденсатом немедленно закрывают пробкой (чтобы состав не изменился) и охлаждают до комнатной температуры в холодной воде.

5. На рефрактометре определяют показатель преломления конденсата. С помощью калибровочного графика определяют его состав. Аналогичные измерения проводят со всеми приготовленными растворами.

6. Результаты всех измерений записывают в табл. 3.8.

Таблица 3.8

Результаты опытов

Температура кипения, ^0С	Показатель преломления	Состав, об. %
До отбора пробы	После отбора пробы	Средняя	Жидкость	Конденсат	Жидкость	Конденсат

По результатам экспериментов на одном листе миллиметровой бумаги строят один под другим 3 графика, сохраняя одинаковый масштаб состава по оси абсцисс:

– калибровочный график (показатель преломления – состав);

– диаграмму кипения − кривую жидкости (Т_кип. – состав жидкости) и кривую пара (Т_кип – состав пара). Для построения кривой жидкости используют температуры кипения до отбора пробы, кривую пара строят по средним значениям температуры кипения (между значениями до и после отбора пробы);

– диаграмму состав пара – состав жидкости.

Работа 3.5. Расчёт и построение диаграммы кипения бинарной смеси в предположении идеальных растворов

Цель работы. Построить диаграмму кипения бинарной смеси в предположении идеальности растворов, используя справочные данные.

Методика выполнения работы. Температурой кипения называют температуру, при которой давление насыщенного пара равно внешнему давлению. При нормальной температуре кипения (при 760 мм рт. ст.) для кипящей смеси жидкостей А и В справедливо равенство:

р_А + р_В = 760

а с учётом закона Рауля (3.1)

Для расчёта давлений пара над чистыми жидкостями при разных температурах ( и ) можно использовать уравнение Клапейрона–Клаузиуса (3.5) в экспоненциальной форме:

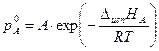и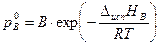

Параметры А, В, Δ_исп Н_А и Δ_исп Н_В находят, решая систему уравнений для двух пар значений р ₁, Т ₁ и р ₂, Т ₂, взятых из справочника [2] (табл. 24, с. 30) для веществ А и В:

(3.26)

Окончательное уравнение для расчёта зависимости температуры начала кипения, т.е. кривой жидкости, от состава смеси имеет вид:

(3.27)

Для расчёта кривой пара помимо закона Рауля

следует использовать закон Дальтона:

.

Отсюда

или для компонента В:

(3.28)

Последовательность выполнения работы

Для расчётов следует выбрать смеси, близкие по свойствам к идеальным: бензол–толуол, толуол–этилбензол, хлорбензол–бромбензол, гексан–гептан, трихлорметан–тетрахлорметан.

1. Выписывают из справочника [2] (табл. 24, с. 30) значения температур кипения чистых жидкостей при 400 и 760 мм рт. ст. и решают систему уравнений (3.26) относительно параметров А, В, Δ_исп Н_А и Δ_исп Н_В.

2. Подставляют численные значения параметров в уравнение (3.27) и решают его относительно . Для удобства построения графика интервал температур следует разбить на 5 - 6 равных интервалов и для каждой температуры вычислить соответствующее ей значение .

3. Подставляют численные значения параметров и соответствующие пары значений Т и в уравнение кривой пара (3.28), вычисляют соответствующие им значения 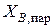. Результаты расчетов заносят в табл. 3.9.

Таблица 3.9

Результаты опытов

T, K
t, ^0C

4. По результатам расчётов строят на миллиметровке диаграмму кипения.

Контрольные вопросы

1. Какой раствор называют идеальным?

2. Укажите признаки образования идеальных растворов.

3. В чём причина отрицательных отклонений от закона Рауля?

4. Сформулируйте и проиллюстрируйте на графике первый закон Коновалова.

5. Сформулируйте и проиллюстрируйте на графике второй закон Коновалова. Что называют азеотропной смесью?

6. Поясните процесс перегонки на диаграмме температура кипения – состав раствора.

3.3.3. Равновесие жидкость – твердая фаза в двухкомпонентных системах

При нагревании смеси двух твёрдых веществ до высокой температуры образуется однородная смесь (раствор). Если такой раствор (или расплав) охлаждать, то при некоторой температуре он начинает кристаллизоваться, поскольку растворимость твёрдых веществ с понижением температуры уменьшается.

Известно 230 видов кристаллических решёток, в которых кристаллизуются все твёрдые вещества. Если два твёрдых вещества имеют одинаковые химический тип строения, кристаллическую решётку и близкий размер частиц, то они образуют твёрдые растворы с неограниченной растворимостью в твердом состоянии. Такие вещества называют изоморфными. При охлаждении смесей изоморфных веществ кристаллизуются твёрдые растворы.

Если описанные выше условия не выполняются, вещества называют неизоморфными. При охлаждении смесей неизоморфных веществ вначале кристаллизуется тот компонент, относительно которого раствор становится насыщенным. По достижении температуры, при которой жидкий раствор становится насыщенным относительно второго компонента, происходит одновременная кристаллизация обоих веществ. Раствор, насыщенный обоими компонентами и имеющий наименьшую температуру кристаллизации, называют эвтектическим.

Каждая фаза двухкомпонентной системы может быть охарактеризована тремя переменными: температурой Т, давлением р и мольной долей Х_i одного из компонентов. Для графического изображения функции f(T, p,X) необходима система координат в пространстве трёх измерений. Откладывая по трем взаимно перпендикулярным осям экспериментальные значения температур, давлений и концентраций, можно построить полную диаграмму состояния данной системы. Однако построение полных диаграмм состояния сопряжено с большими экспериментальными трудностями и пока осуществимо лишь для немногих систем. Если система конденсирована, то небольшие изменения давления мало отражаются на равновесии. Поэтому при исследовании конденсированных систем при атмосферном давлении можно без ощутимой погрешности принять давление постоянным. Если рассматривать свойства системы при р = const и выбрать это давление большим, чем давление насыщенных паров смесей любого состава, то в системе не будет газообразной фазы. Число переменных уменьшится до двух. Графически зависимость между ними может быть выполнена на плоскости в координатах Т - X. Построенную диаграмму называют диаграммой состояния или диаграммой плавкости.

Диаграммы состояния изображают равновесия между всеми жидкими и твердыми фазами, образуемыми компонентами системы при различных концентрациях и температурах и постоянном давлении. При построении этих диаграмм системы изучаются во всем интервале концентраций, т.е. от чистого вещества А до чистого вещества В. Интервал температур, в котором проводится исследование, выбирается так, чтобы на диаграмме отражалось как равновесие жидких фаз с другими жидкими и твёрдыми фазами, так и превращения, протекающие в системе ниже температуры её полного затвердевания.

Для построения диаграмм плавкости обычно используют метод термического анализа (или дифференциально-термического анализа), суть которого заключается в определении температур при равновесии между жидкими и твердыми фазами. Метод не требует ни механического разделения фаз, ни их химического анализа. Для осуществления термического анализа необходима техническая возможность регистрации изменения температуры от времени при постепенном охлаждении исследуемой системы, т.е. получения кривых охлаждения (рис. 3.10). Вид кривых охлаждения зависит от типа и состава смеси.

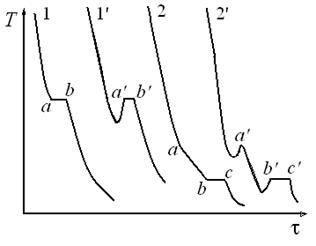
Рис. 3.10. Вид кривых охлаждения

При охлаждении системы скорость понижения температуры пропорциональна разности температур системы Т_с и окружающей среды Т_ср, т.е. определяется уравнением вида:

(3.29)

Из уравнения (3.29) следует, что кривая охлаждения должна быть вогнута к оси времени τ. При большой разности температур она близка к прямой линии. Кристаллизация расплавленного индивидуального вещества, подвергнутого медленному охлаждению, вызывает температурную остановку (отрезок ab на кривой 1, рис. 3.10), так как состав жидкой фазы остаётся неизменным и выделяющаяся теплота кристаллизации полностью компенсирует отвод теплоты в окружающую среду. На кривой охлаждения моменту выделения первого кристалла отвечает точка а. Длительность температурной остановки (размер горизонтального участка на кривой охлаждения) зависит от количества вещества и от скорости отвода тепла. При исчезновении последней капли жидкости (точка b на кривой 1) температура вновь начинает понижаться, поскольку с этого момента потеря теплоты в окружающую среду уже ничем не возмещается.

При охлаждении расплава двухкомпонентной неизоморфной смеси отвердевание начинается с кристаллизации того из компонентов, относительно которого жидкий раствор становится насыщенным. На кривой охлаждения 2(рис. 3.10) показано, что в точке a кристаллизация одного компонента приводит к излому кривой и уменьшению скорости охлаждения вследствие выделения теплоты плавления. Отсутствие температурной остановки объясняется тем, что состав жидкой фазы при кристаллизации одного из компонентов непрерывно меняется. Каждому новому составу соответствует своя (более низкая) температура кристаллизации.

По достижении температуры, при которой жидкий раствор становится насыщенным относительно второго компонента, происходит одновременная кристаллизация веществ. Раствор, насыщенный обоими компонентами и имеющий наименьшую температуру кристаллизации, называют эвтектическим. При кристаллизации эвтектики состав жидкой фазы остаётся постоянным, поэтому на кривой охлаждения 2 наблюдается температурная остановка (отрезок вс). После отвердевания всей смеси (точка с на кривой 2) температура снова понижается.

Кривые 1 и 2 на рис. 3.10 представляют идеальный вид кривых охлаждения, которые наблюдаются при кристаллизации смесей, состоящих из простых веществ, например, металлов и их сплавов. Сложные вещества и их смеси, в частности, органические, как правило, кристаллизуются с переохлаждением, величина которого зависит от чистоты вещества и условий охлаждения. Это приводит к более сложной форме кривых охлаждения (кривые 1' и 2' на рис. 3.10). В качестве температуры начала кристаллизации в этих случаях следует взять температуру, соответствующую точке a׳, а в качестве температуры конца кристаллизации – температуру точки b׳.

Диаграмма плавкости. Ординаты точек a и b или a' и b' на рис. 3.10, то есть температуры начала и конца кристаллизации зависят от состава исходной смеси. Эта зависимость, выраженная графически в координатах температура – состав, носит название диаграммы плавкости.

  T

На рис. 3.11 изображён общий способ построения диаграммы плавкости двухкомпонентных неизоморфных смесей с одной эвтектикой.

Рис. 3.11. Построение диаграммы плавкости (а) по кривым охлаждения (б)

В этой системе компоненты в жидкой фазе неограниченно растворимы друг в друге и совсем не растворимы в твердом состоянии. Точки 2 – 4соответствуют составам смесей, а точки a_n и b_n – температурам начала и конца кристаллизации этих смесей. Проводя сплошные линии через точки a_n и b_n, получают диаграмму плавкости.

Линию, соединяющую точки a_n, называют ликвидусом. Она представляет собой геометрическое место точек, соответствующих температурам начала кристаллизации. Следовательно, поле диаграммы выше линии ликвидуса отвечает области условий существования системы в жидком состоянии.

Линию, соединяющую все точки b_n, называют солидусом. Она представляет собой геометрическое место точек, соответствующих температурам конца кристаллизации. Ниже линии солидуса на диаграмме вся система находится в твёрдом состоянии. Поскольку неизоморфные вещества не образуют твёрдых растворов, каждое вещество отвердевает в своей кристаллической форме. Другими словами, ниже линии солидуса мы имеем двухфазную твердую систему (смесь кристаллов А и В).

Треугольник Таммана. При построении диаграммы плавкости по кривым охлаждения возникает вопрос о координатах эвтектической точки Э. Тамман заметил, что длительность температурной остановки на кривой охлаждения прямо пропорциональна количеству эвтектики в исходной смеси. Максимальную температурную остановку при кристаллизации имеет смесь эвтектического состава (точка Э).

Отложив длину отрезков b_nc_n (рис. 3.11б) (продолжительность температурных остановок) как функцию состава смеси, Тамман получил две прямые, пересекающиеся при составе, имеющем наибольшую длительность температурной остановки, т.е. при составе эвтектики (точка Э, рис. 3.11а). Из рис. 3.11а видно, что получившаяся фигура имеет вид треугольника. Поэтому определение состава эвтектики по температурным остановкам на кривых охлаждения носит название метода построения треугольника Таммана.

Работа 3.6. Построение диаграммы плавкости неизоморфной смеси по кривым охлаждения

Цель работы. Построить диаграмму плавкости по кривым охлаждения и определить состав эвтектики методом построения треугольника Таммана.

Методика выполнения работы. Для изучения кристаллизации из растворов ряд смесей исследуемых веществ с различным составом помещают в пробирки и нагревают в водяной бане до расплавления. Температуру исследуемых смесей измеряют с помощью хромель-копелевых термопар (ХК). Термопара состоит из спаянных на концах хромелевой и копелевой проволок. Один спай (горячий) помещают в исследуемую смесь, а другой (холодный) подключают к компенсационной схеме автоматического самопишущего потенциометра КСП-4. На концах термопары возникает термоЭДС, величина которой прямо пропорциональна разности температур на концах горячего и холодного спаев. Шкала потенциометра отградуирована в градусах Цельсия. В момент компенсации стрелка потенциометра показывает температуру исследуемой системы, а регистрирующее устройство печатает на диаграммной ленте точку с номером. Наличие в приборе переключателя позволяет измерять и регистрировать параллельно температуры 6-ти исследуемых смесей с интервалом 20 с.

Дата добавления: 2017-02-01