Определение составов сопряжённых слоёв

Если показатель преломления одного из компонентов значительно отличается по величине от показателей преломления других компонентов, то для анализа составов сопряжённых слоёв удобно использовать предварительно построенный калибровочный график в координатах показатель преломления n – состав тройной системы, полученной в результате титрования (три кривые на одном графике). Для построения калибровочного графика необходимо измерить показатели преломления всех тройных смесей, полученных в результате титрования (порядок работы на рефрактометре описан в Приложении 1). Составы тройных смесей рассчитывают по положению точек на изотерме растворимости. Результаты заносят в табл. 3.10.

Таблица 3.10

Результаты опытов

Бинарная смесь до титрования, об. %	Тройная смесь после титрования, об. %	Показатель преломления, n
А	С	В	А	С

После проверки графика у преподавателя следует получить контрольную гетерогенную смесь исследуемых жидкостей. Смесь необходимо тщательно перемешать и разделить с помощью делительной воронки. (Полное разделение смеси на два прозрачных слоя может потребовать 1-2 ч). Измерив показатели преломления нижнего и верхнего слоёв жидкости, определяют по калибровочному графику их составы. Точки, отвечающие составам сопряжённых слоёв, наносят на изотерму растворимости. Линия, соединяющая эти точки, при надлежащем выполнении работы должна проходить через точку, соответствующую составу контрольной смеси. В таком случае она действительно является коннодой.

Контрольные вопросы

1. Как определить состав трёхкомпонентной смеси на концентрационном треугольнике методом Гиббса?

2. Как определить состав трёхкомпонентной смеси на концентрационном треугольнике методом Розебома?

3. Какими свойствами обладают смеси, точки составов которых лежат на прямых, (а) параллельных стороне концентрационного треугольника, (б) исходящих из вершины концентрационного треугольника?

4. Сформулируйте и проиллюстрируйте на концентрационном треугольнике правило Тарасенкова.

Глава 4. Электрохимия

4.1. Растворы электролитов в равновесных условиях

Электролиты – химические соединения, которые в растворе или расплаве самопроизвольно частично или полностью распадаются на про­тивоположно заряженные ионы – катионы и анионы.

Электролитическая диссоциация – процесс распада вещества на ионы. Диссоциации подвергаются вещества, содержащие как ионы, так и молекулы в своей структуре. Электролитическая диссоциация в растворе происходит вследствие взаимодействия молекул растворителя с частицами вещества. Величина и знак заряда ионов, образующихся при диссоциации одной молекулы электролита, определяются стехиометрическими коэффициентами в формуле молекулы. В зависимости от числа образующихся ионов ν различают следующие типы электролитов:

· бинарные, распадающиеся на два иона:

1 – 1 (оба иона однозарядные – NaCl)

2 – 2 (оба иона двухзарядные – ZnSO₄)

· тернарные, распадающиеся на три иона:

1 – 2 (одно-, двухзарядные ионы – Na₂SO₄)

2 – 1 (двух-, однозарядные ионы – CaCl₂)

· квартернарные, распадающиеся на четыре иона:

1 – 3 (одно-, трёхзарядные ионы – K₃PO₄)

3 – 1 (трёх-, однозарядные ионы – Al(NO₃)₃)

Одни и те же электролиты могут диссоциировать по-разному в зависимости от условий: природы растворителя, температуры, концентрации, присутствия примесей и т.д. Как правило, в большей степени электролиты диссоциируют в растворителях с высокой диэлектрической проницаемостью (для воды e = 78,3) и практически не диссоциируют в растворителях с малой диэлектрической проницаемостью (для бензола e = 2 – 3). Поэтому электролиты условно разделяют на две группы: сильные и слабые.

С ильные электролиты диссоциируют в растворе любых концентраций практически полностью. Образующиеся ионы взаимодействуют между собой. Силы взаимодействия электростатические и зависят от расстояния между ионами;

С лабые электролиты диссоциируют в растворе частично. Образующиеся ионы удалены друг от друга на значительные расстояния и не взаимодействуют между собой.

4.1.1. Слабые электролиты

Процесс диссоциации слабых электролитов – равновесный обрати­мый процесс:

↔ ,

в котором недиссоциированные молекулы находятся в динамическом рав­новесии с образовавшимися ионами. Количественной характеристикой этого процесса является константа электролитической диссоциацииК_с (константа равновесия процесса диссоциации):

,

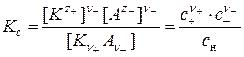где с ₊, с _–, с _н – равновесные концентрации катионов, анионов и недиссо­циированных молекул соответственно; z ₊, z _– – заряды катионов и анионов; ν ₊, ν _– – число катионов и анионов в одной молекуле электролита.

Константа диссоциации может принимать любые положительные значения. Она является величиной постоянной (при постоянной темпера­туре) и не зависит от присутствия посторонних электролитов и концентра­ции электролита, если растворы достаточно разбавленные и обладают свойствами идеальных растворов.

Более концентрированные растворы электролитов обладают свойст­вами неидеальных растворов, и для них К_с = f(c). Поэтому в этих случаях в выражении константы диссоциации для растворов любых концентраций при T = const используется термодинамическая величина активность (по Льюису):

,

где а₊ = γ ₊·с₊ – активность катионов, а _– = γ_– ·с _– – активность анионов, а_н = γ _н·с_н – активность недиссоциированных молекул, γ₊, γ_–, γ_н – коэффициенты активности катионов, анионов, недиссоциированных молекул соответст­венно, К_а – истинная термодинамическая константа диссоциации.

Константа диссоциации зависит от природы электролита, природы растворителя и температуры. Зависимость константы диссоциации от тем­пературы выражается уравнением изобары Вант-Гоффа:

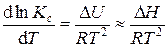, (4.1)

где Δ H ≈ Δ U – тепловой эффект процесса диссоциации, поскольку при дис­социации p Δ V ≈ 0. В широком интервале температур зависимость константы диссоциа­ции от температуры может иметь вид, представленный на рис. 4.1.

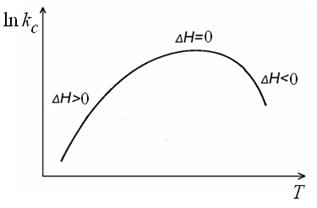
Рис.4.1. Зависимость константы диссоциации слабых электролитов (уксусная, муравьиная кислоты) от температуры.

Другой количественной характеристикой процесса диссоциации является степень электролитической диссоциации a – отношение числа N _д (концентрации) молекул, распавшихся на ионы, к общему числу N (кон­центрации) растворённых молекул:

,

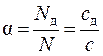где c – концентрация растворенных молекул, с _д = a ×с – концентрация продиссоциированных молекул. Концентрация недиссоциированных молекул:

с _н = с – с _д = с – a ×с = с(1 – a )

Степень диссоциации меняется в пределах 0 < α < 1 и зависит от:

– природы электролита (α → 0 – слабые электролиты, α → 1 – сильные электролиты);

– природы растворителя: чем выше диэлектрическая проницаемость растворителя, тем больше α;

– присутствия посторонних электролитов: α возрастает с ростом концентрации постороннего электролита;

– температуры: α может возрастать, падать или оставаться постоянной при повышении температуры;

– концентрации электролита: при уменьшении концентрации раствора α увеличивается и при бесконечном разбавлении α → 1.

Константа диссоциации и степень диссоциации взаимосвязаны друг с другом:

если ν₊ = ν_– = 1, то

(4.2)

Учитывая, что – разбавление (объем раствора, в кото­ром растворен 1 моль вещества), выражение (4.2) можно записать в виде:

(4.3)

Уравнение (4.3) носит название закона разбавления Оствальда.

4.1.2. Сильные электролиты

В растворах сильных электролитов каждый ион (центральный) ок­ружен ионами разных знаков (ионной сферой). Вследствие взаимодействия ионов растворы сильных электролитов любых концентраций являются не­идеальными, и для описания их свойств используется активность а. На отклонение от идеальности влияют как катионы, так и анионы и не пред­ставляется возможным учесть это влияние порознь. По этой причине ввели понятие о средней ионной активности а_±:

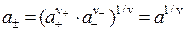
С другой стороны:

,

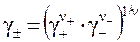где g_± - средний ионный коэффициент активности ионов, γ ₊ – коэффициент активности катионов; γ _– – коэффициент активности анионов, ν₊ – число катионов в молекуле; ν _– – число анионов в молекуле; ν = ν₊ + ν _– – общее число ионов в молекуле

Средняя ионная моляльная концентрация m _±:

,

где m₊= v ₊·m – моляльная концентрация катионов; m _– = v_– ·m – моляльная концентрация анионов; m – моляльная концентрация раствора;.

Среднее число ионов в молекуле

Активность и коэффициент активности зависят от природы электролита, природы растворителя, температуры, давления, концентрации вещества и примесей и учитывают взаимодействие всех частиц в растворе при равновесии.

Зависимость коэффициента активности от этих факторов описыва­ется уравнениями предельного закона Дебая–Хюккеля:

(4.4)

где I - ионная сила раствора, зависящая от концентрации и заряда всех ионов в растворе

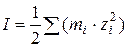
A – величина, зависящая от диэлектрической проницаемости растворителя ε и температуры Т.

Для водных растворов при 298 К А = 0,509.

Уравнения (4.4) справедливы для разбавленных растворов электролитов при m ≤ 0,01 - 0,03 моль/1000 г растворителя.

Константа равновесия процесса растворения т.е. фазового равнове­сия твёрдого вещества (обычно малорастворимой соли) с его насыщенным раствором:

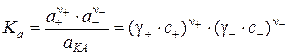, (4.5)

где а_КА = 1 – активность нерастворённой соли, записывается как произве­дение активностей ионов. Эту величину называют произведением рас­творимости L:

Коэффициенты активности ионов в разбавленных растворах, т.е. при малой растворимости электролита, можно принять за единицу, тогда L определяется как произведение равновесных концентраций (молярных или моляльных) ионов:

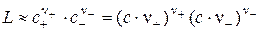(4.6)

Так как концентрации ионов – это растворимость S электролита в насыщенном растворе, то уравнение (4.6) можно записать в виде:

L» (n ⁺S)ⁿ⁺∙(n ^-S)^n-

Зависимость растворимости от температуры передается уравнением:

, (4.7)

где Δ Н° - теплота растворения соли.

После интегрирования (4.7) получаем:

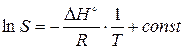(4.8)

Т.е. величину Δ Н° можно определить из тангенса угла a наклона прямой на графике зависимости ln S от (Δ Н° = – R×tg a). При интегрировании уравнения (4.7) в интервале температур от Т ₁ до Т ₂ получаем:

(4.9)

Константа равновесия процесса растворения связана с изменением энергии Гиббса Δ G°:

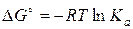(4.10)

Зная Δ G° и Δ Н° можно вычислить изменение энтропии Δ S° в процессе растворения:

Δ G° = Δ Н° – T ∙Δ S° (4.11)

4.2. Растворы электролитов в неравновесных условиях

4.2.1. Электрическая проводимость растворов электролитов

Растворы электролитов проводят электрический ток. Носителями электричества являются противоположно заряженные ионы, образую­щиеся в процессе диссоциации. Величину, обратную электрическому со­противлению раствора R, называют его электрической проводимостью. Удельная электрическая проводимость χ – электропроводимость объема раствора электролита, заключенного между двумя параллельными элек­тродами площадью S = 1 см², расположенными на расстоянии l = 1 см друг от друга:

,

где – удельное сопротивление.

Тогда:

При наложении электрического поля возникает упорядоченное дви­жение ионов к противоположно заряженным электродам (катоду и аноду). Катионы и анионы передвигаются к электродам с постоянной, но различ­ной скоростью.

Скорость движения иона w_i прямо пропорциональна разности потен­циалов между электродами Δ U, заряду иона z_i и обратно пропорциональна вязкости среды η, расстоянию между электродами l и радиусу сольватиро­ванного иона r_i. Скорость движения катиона w ₊ (м/с):

скорость движения аниона w _- (м/с):

,

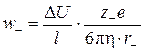где е = 1,602·10^–19 Кл – элементарный электрический заряд.

Скорость движения ионов при градиенте потенциала 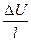=1 В/м на­зывают подвижностью ионов и (м²/(В·с)):

– катионов

– анионов

Применительно к растворам электролитов заданной концентрации величины:

L ₊ = F·×z₊×и₊ и L_– = F×z_-·и _– [См·м²/моль]

l ₊ = F·и₊ и l_– = F×и _–[См·м²/моль-экв]

называют молярными L (эквивалентными l ) электрическими прово­димостями ионов. Применительно к предельно разбавленным растворам электролитов величины:

F×z₊×и₊ ⁰ = L ₊ ⁰ и F×z_-·и _–⁰ = L_–⁰[См·м²/моль]

F×и₊ ⁰ = l₊ ⁰и F·и _–⁰ = l _–⁰[См·м²/моль-экв]

называют предельными молярными L⁰ (эквивалентными l⁰ ) электриче­скими проводимостями ионов, а величины и₊⁰ и и _– ⁰ – предельными подвижностями ионов.

Молярная электрическая проводимость L [См·см²/моль] – элек­тропроводимость объёма раствора электролита, содержащего 1 моль рас­творенного вещества и заключённого между двумя параллельными элек­тродами, расположенными на расстоянии l = 1 м друг от друга.

Эквивалентная электрическая проводимость l [См·м²/(моль-экв)] - электропроводимость объема раствора электролита, содержащего 1 моль-экви­валент растворенного вещества и заключенного между двумя параллель­ными электродами, расположенными на расстоянии l = 1 м друг от друга.

Удельная, молярная и эквивалентная электропроводимости связаны между собой соотношениями:

, (4.12)

где с выражена в моль/л, а с ^* - моль-экв/л, c - См×см^-1.

Молярная и эквивалентная электрические проводимости растворов сильных и слабых электролитов связаны с соответствующими электриче­скими проводимостями ионов соотношениями:

L = a(n₊L₊ + n_-L_-)

l = a(l₊ + l_-),

а при предельном разбавлении (a = 1):

L⁰ = n₊L₊⁰ + n_-L_-⁰

l⁰ = l₊⁰ + l_-⁰ (4.13)

Уравнение (4.13) выражает закон независимого движения ионов Коль­рауша. Величины L₊⁰ и λ _- ⁰ являются постоянными для каждого иона и за­висят только от природы растворителя и температуры, их значения приводятся в справочниках.

На электрическую проводимость растворов электролитов влияют многие факторы: природа электролита, природа растворителя, концентра­ция посторонних ионов, температура, концен­трация электролита и т.п.

Зависимость электропроводимости от концентрации. Удельная электрическая проводимость разбавленных растворов сильных и слабых электролитов сначала линейно возрастает по мере увеличения концентрации электролита. Это является следствием увеличения в исследуемом рас­творе числа ионов – носителей электрического тока (рис. 4.2).

Рис. 4.2. Зависимость удельной электропроводимости от концентрации растворов электролитов

Дальнейшее увеличение концентрации сильного электролита приво­дит к снижению удельной электрической проводимости из-за электроста­тического межионного взаимодействия; в растворах слабых электролитов – из-за ассоциации ионов и образования нейтральных молекул. Положение максимума на кривых χ– с определяется температурой и природой электролита.

Эквивалентная и молярная электрические проводимости растворов сильных и слабых электролитов возрастают по мере разбавления раство­ров: у слабых электролитов – вследствие увеличения степени диссоциации, у сильных электролитов – вследствие уменьшения электростатического взаимодействия между ионами (рис. 4.3).

Рис.4.3. Зависимость эквивалентной электропроводимости от концентрации растворов электролитов

При бесконечном разбавлении (с → 0, а V → ∞) эквивалентная электрическая проводимость достигает предельного значения – λ ⁰.

Для разбавленных растворов слабых электролитов (a → 0) отношение:

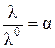(4.14)

При диссоциации электролита по схеме:

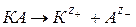
константа диссоциации:

(4.15)

или (после преобразования):

,

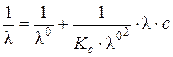т.е. имеет место линейная зависимость в координатах 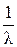- l×С (рис. 4.4) с тангенсом угла наклона прямой .

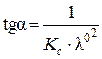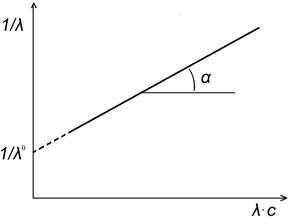
Рис. 4.4. Графический метод определения λ^∞ и К_с

Для более концентрированных растворов (или при α << 1)

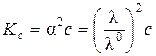или ,

т.е. имеет место линейная зависимость в координатах l - 1/ .

При отклонении растворов от идеальности в расчетах термодинами­ческой константы диссоциации используется активность частиц:

Учитывая, что коэффициент активности недиссоциированных (неза­ряженных) частиц γ _КА = 1, а γ₊·γ_– = γ_±². Средний ионный коэффициент ак­тивности γ_± рассчитывается по уравнению Дебая–Хюккеля:

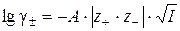
Тогда связь К_а и К_с будет иметь вид:

К_а = К_с· γ _± ²

Для растворов сильных электролитов (a = 1)

, (4.16)

где f _λ – коэффициент электропроводимости, учитывающий взаимодейст­вие всех ионов в растворе при пропускании тока через раствор.

Для предельно разбавленных растворов сильных электролитов (с ≤ 0,02 моль-экв/л) зависимость l (или L) от концентрации описывается уравнением Кольрауша (закон квадратного корня):

, (4.17)

т.е. имеет место линейная зависимость в координатах (рис. 4.5) с тангенсом угла наклона прямой tgα = –A.

,

где А – эмпирический коэффициент, зависящий от температуры, природы электролита и растворителя.

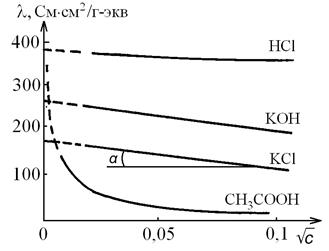
Рис. 4.5. Зависимость эквивалентной электропроводимости от квадратного корня из концентрации

Для водного раствора электролита типа 1–1 с вязкостью η = 8,9·10^–4 Па·с, диэлектрической проницаемостью при Т = 298 К

А = 60,64 + 0,2273 λ⁰ (4.18)

Согласно теории сильных электролитов Дебая–Хюккеля, каждый ион окружён ионами противоположного знака (ионной атмосферой). При наложении внешнего электрического поля центральный ион и ионная атмосфера, обладающие равными по величине, но обратными по знаку зарядами, движутся в противоположных направлениях. Из-за электростатического взаимодействия центрального иона с ионной атмо­сферой происходит торможение движения иона (электрофоретический эффект).

Под действием внешнего поля центральный ион смещается относи­тельно центра ионной атмосферы. Избыточный заряд сферы, оставшейся позади движущегося иона, тормозит его движение (релаксационный эффект). Оба эффекта торможения вызывают уменьшение эквивалентной электрической проводимости раствора и учитываются коэффициентом А в уравнении Кольрауша (4.17).

Зависимость электропроводимости от температуры. Электропроводимость растворов электролитов увеличивается с ростом темпера­туры. Это является следствием того, что при повышении температуры уве­личивается степень диссоциации и скорость движения ионов, уменьшается гидратация ионов и вязкость раствора.

Зависимость вязкости раствора η _Т от температуры выражается урав­нением:

,

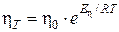где η₀ – константа (вязкость раствора при Т → ∞); Е _η– энергия активации процесса вязкого течения жидкости, Дж/моль.

В интегральной форме:

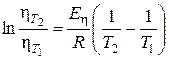(4.19)

В узком интервале температур зависимость эквивалентной и удель­ной электрической проводимости от температуры можно представить уравнениями:

λ _Т = λ₂₉₈[1 + a(T – 298) + β(T – 298)²]

, (4.20)

где 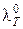– эквивалентная электрическая проводимость при бесконечном разбавлении.

χ _T = χ ₂₉₈ [1 + α(T – 298) + β(T – 298)²],

где α, β – температурные коэффициенты электрической проводимости, зависящие от природы электролита.

При условии, что β ≈ 0:

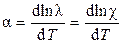
Для сильных кислот a = 0,0164, для сильных оснований a = 0,019, для солей a = 0.022.

В широком интервале температур зависимость эквивалентной электрической проводимости от температуры выражается уравнениями:

– в дифференциальной форме:

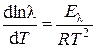
– в интегральной форме:

, (4.21)

или

, (4.22)

где А – константа, не зависящая от температуры (λ при Е_l → 0); Е _λ – энергия активации процесса электрической проводимости (Дж/моль).

После определённого интегрирования в пределах от Т ₁ до Т ₂ получаем:

, (4.23)

где Е _λ = α ·RT ².

Зависимость удельной электрической проводимости от температуры проходит через максимум, который определяется концентрацией, типом электролита и природой растворителя.

4.2.2. Методика измерения электрической проводимости

растворов электролитов

Измеряемой величиной является сопротивление R раствора электролита. Во избежание процессов электролиза ток в цепи в момент измерения протекать не должен. Это реализуется в компенсационной электрической схеме, называемой мостом Кольрауша (рис. 4.6).

Рис. 4.6. Компенсационная схема для измерения электропроводимости растворов электролитов:

1 – электрохимическая ячейка (с двумя электродами); 2 – источник переменного тока высокой частоты (2000-3000 Гц); 3 – нуль-прибор; 4,5 – известные переменные сопротивления R ₀, R ₁, R ₂

Схема работает по методу компенсации. Электрохимическая ячейка термостатирована, электроды, площадью S, расположены неподвижно на расстоянии l друг от друга. Ячейка заполнена раствором электролита, обладающим сопротивлением R_x. Источник переменного тока высокой частоты (2000-3000 Гц) применяется во избежание процессов электролиза. Согласно закону Кирхгофа, ток в цепи до разветвления равен сумме токов после разветвления:

I = I ₁ + I ₂

Величины токов регулируются сопротивлениями R ₁, R ₂, R ₀ так, чтобы на участке АВ в цепи ток стал равным нулю (скомпенсировался). В этих условиях падения напряжения в ветвях цепи станут равными:

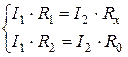
Решая систему уравнений, можно найти сопротивление

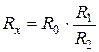
По сопротивлению R_x рассчитывается удельная электропроводимость раствора:

(4.24)

Входящая в уравнение (4.24) величина

(4.25)

называется постоянной прибора (константой ячейки): это удельная электропроводимость раствора с сопротивлением 1 Ом. Константа ячейки φ определяется каждый раз по раствору с известной удельной электропроводимостью (0,02 н KCl):

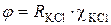(4.26)

Современные измерительные приборы сконструированы по принципу работы моста Кольрауша. С их помощью можно измерять либо сопротивление раствора R, либо удельную электропроводимость χ.

Работа 4.1. Зависимость электрической проводимости растворов слабых электролитов от концентрации

Цель работы. Исследовать зависимость электрической проводимости (c, L или l) от концентрации растворов слабого электролита, из полученных экспериментальных данных вычислить эквивалентную электропроводность при бесконечном разведении l⁰ и константу диссоциации К_С, сравнить полученные значения с табличными.

Дата добавления: 2017-02-01