Последовательность выполнения работы

1. Включают нагреватель водяной бани в сеть.

2. Помещают в водяную баню комплект пробирок с исследуемыми смесями и опущенными в них термопарами.

3. Включают автоматический потенциометр КСП-4 в сеть, тумблер «прибор» на передней панели КСП-4 переводят в положение «вкл». В процессе нагревания смеси в пробирках расплавляются, а указатель на шкале прибора перемещается от комнатной температуры до 95 ^оС.

4. По достижении температуры 95 ^оС тумблер «диаграмма» на передней панели прибора переключают в положение «вкл».

5. Из бани последовательно с интервалом 10 мин вынимают пробирки со смесями №№ 1,2,3,4 и т.д. и ставят охлаждаться в соответствующие гнезда в стеклянном стакане. Нагреватель водяной бани в это время выключают из сети. Прибор записывает кривые охлаждения таким образом, что каждой точке с цифрой на диаграммной ленте соответствует температура в пробирке с тем же номером в определённый момент времени.

6. После охлаждения пробирок с исследуемыми смесями до комнатной температуры, тумблеры «диаграмма» и «прибор» ставят в положение «откл».

7. Аккуратно отрывают диаграммную ленту с записью кривых охлаждения и по данным этих кривых выполняют следующие задания по указанию преподавателя:

По экспериментальным кривым охлаждения определяют значения температур начала Т _н.к. и конца Т _к.к. кристаллизации, а также длительность температурной остановки (в мм по диаграммной ленте) для всех изученных смесей и заносят их в табл. 3.10.

Таблица 3.10

Результаты опытов

Состав, мас. %	Состав, мол. %	Т н.к., ^оС	Т к.к., ^оС	Длительность температурной остановки, мм

На листе миллиметровой бумаги строят диаграмму плавкости в координатах температура – состав. Через точки температур конца кристаллизации проводят линию солидуса.

С помощью треугольника Таммана, построенного под диаграммой, определяют состав эвтектики и переносят его на линию солидуса, как это показано на рис. 3.11а. Далее проводят плавные линии ликвидуса.

Работа 3.7. Расчёт и построение диаграммы плавкости

неизоморфной смеси в предположении идеальных растворов

Цель работы. Построить диаграмму плавкости неизоморфной смеси для идеальных растворов

Методика выполнения работы. Растворимость твердых веществ в жидкостях описывается уравнением Шредера:

(3.30)

Интегрирование уравнения (3.30) даёт зависимость растворимости твёрдых веществ в жидкостях от температуры в случае образования идеальных растворов.

Расчёт координат эвтектики. На рис. 3.11а кривые Т_А Э и Т_В Э отвечают насыщенным растворам относительно кристаллов А и В соответственно, т.е. Т_А Э представляет собой кривую растворимости кристаллов А в жидкости, а Т_В Э – кристаллов В. В предположении идеальности растворов и независимости теплоты плавления от температуры [ ] кривые Т_А Э и Т_В Э можно описать уравнением Шредера

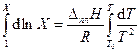
В качестве нижнего предела интегрирования выбираем параметры чистого вещества, для которого Х = 1, а Т = Т ₀. После интегрирования получаем уравнение Шредера в интегральной форме:

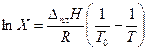(3.31)

Из уравнения (3.31) следует, что растворимость увеличивается с температурой по экспоненте. Таким образом, кривая Т_А Эописывается уравнением

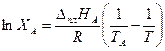(3.32)

а кривая Т_В Э– уравнением

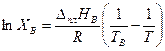, (3.33)

где 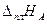, – теплоты плавления чистых веществ А и В; Т_А, Т_В – температуры плавления чистых веществ А и В.

Поскольку точка Э принадлежит обеим кривым (Х _Э характеризует раствор, насыщенный относительно обоих компонентов), её координаты можно определить совместным решением уравнений (3.32) и (3.33). Обозначив координаты общей точки Х_В = 1− Х_А = Х_Э, Т = Т_Э, получаем систему двух уравнений с двумя неизвестными:

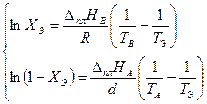
Найдём из этих уравнений величину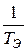

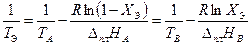(3.34)

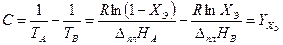(3.35)

Полученное логарифмическое уравнение (3.35) решается численными методами (золотого сечения, половинного деления и т.д.). В отсутствии компьютера можно использовать метод подбора, по которому вычисляют значения правой части уравнения Y (X_Э) (3.35) по крайней мере при двух значениях аргумента X и сравнивают с величиной С. Если последняя находится между вычисленными значениями функции Y(X ₁ ) и Y(X ₂ ), то линейной интерполяцией находят значение Х, при подстановке которого в уравнение получается величина С. Эту операцию удобно проводить графически (рис. 3.12). Для этого рассчитывают несколько значений (не менее 4) правой части выражения, обозначенной Y при различных значениях Х и строят график зависимости Y = f (Х_В), как показано на рис. 3.12.

Рис. 3.12. Графическое решение уравнения (3.35)

После этого откладывают на оси ординат значение левой части уравнения (3.15) 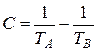и графически находят соответствующее ему значение абсциссы Х _Э. Температуру эвтектики Т _Э рассчитывают по уравнению (3.34) после подстановки найденного выше состава эвтектики Х _Э. Данные для расчёта диаграммы плавкости следует выбрать из таблицы Приложения 2 (по указанию преподавателя).

Расчёт кривых ликвидуса. После определения координат точки эвтектики можно рассчитать обе ветви кривой ликвидуса. Для этого в уравнении (3.32) надо задаваться различными значениями Х_А между 1 и Х _Э и рассчитывать соответствующие им значения температуры Т. Таким образом можно построить кривую Т_А Э.

Аналогично можно построить кривую Т_В Э. Для этого надо использовать уравнение (3.33). Построив рассчитанные кривые Т_А Э и Т_В Э и проведя через точку Э линию солидуса (при постоянной температуре Т _Э), получим диаграмму плавкости, рассчитанную в предложении идеальности жидких растворов неизоморфных веществ А и В и независимости теплот плавления от температуры.

Расчёт теплоты плавления по данным термического анализа. Если известны температуры кристаллизации двух растворов разного состава, то с помощью уравнения Шредера можно рассчитать теплоту плавления кристаллизующегося вещества.

Обычно в качестве одной жидкости выбирают чистое вещество (Х ₁ = 1), а в качестве второй жидкости – раствор, содержащий небольшое количество другого вещества. Тогда из уравнений (3.32) и (3.33) следует

.

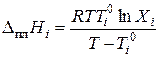Контрольные вопросы

1. Что называется компонентом, фазой и числом термодинамических степеней свободы данной системы?

2. Привести примеры и раскрыть смысл линий и полей на диаграмме плавкости изоморфных и неизоморфных веществ.

3. По диаграмме плавкости неизоморфных веществ поясните сущность термического анализа. Начертите типичные кривые охлаждения.

4. Что такое эвтектическая смесь?

5. Напишите уравнение Шредера и раскройте физический смысл входящих в него величин.

6. Укажите методы определения координат эвтектической точки.

3.4. Фазовое равновесие в трёхкомпонентных системах

Для построения полной диаграммы состояния трёхкомпонентной системы нужна система из пяти взаимно перпендикулярных координат: температура, давление, мольные объёмы различных фаз и мольные доли первого и второго компонентов, входящих в состав этих фаз. Построить подобную диаграмму невозможно. С целью упрощения часто принимают постоянными температуру, давление и мольные объёмы. Тогда свойства системы можно изображать с помощью плоской диаграммы, представляющей равносторонний треугольник – концентрационный треугольник Гиббса–Розебома (рис. 3.13).

Вершины равностороннего треугольника отвечают содержанию в системе 100 % каждого из компонентов А, В и С. Стороны треугольника позволяют описать составы двухкомпонентных систем: (А+В), (В+С) и (А+С). Точки, лежащие внутри треугольника, описывают составы трёхкомпонентных систем.

По методу Гиббса соотношения между компонентами определяются на основании того, что сумма перпендикуляров, опущенных из любой точки на стороны треугольника, равна её высоте (100 %) (рис. 3.13а).

По методу Розебома для определения состава системы используют отрезки трёх прямых, параллельных сторонам треугольника и проходящих от данной точки до пересечения с каждой из сторон треугольника (рис. 3.13б). Сумма, построенных таким образом отрезков для любой точки внутри треугольника, равна длине его стороны (100 %).

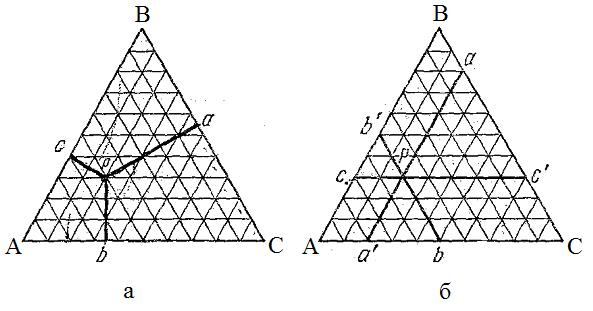
Рис. 3.13. Концентрационный треугольник Гиббса – Розебома для выражения состава и свойств трехкомпонентной системы:

а – метод Гиббса, б – метод Розебома.

Линии, параллельные одной из сторон треугольника (например, стороне АВ), представляют собой геометрические места точек, соответствующие смесям с одинаковым содержанием одного из компонентов (С). Линии, проведенные из вершины треугольника (например, вершины А) до пересечения с противоположной стороной (ВС), представляют собой геометрические места точек, соответствующие системам, в которых отношение концентраций двух компонентов одинаково.

В трёхкомпонентных системах существует большое количество вариантов взаимной растворимости – от неограниченной взаимной растворимости всех трёх жидкостей (вода − этанол − ацетон) до абсолютной нерастворимости (вода − бензол − ртуть). Большой практический интерес представляют системы с ограниченной растворимостью в жидком состоянии. На рис. 3.14 представлена диаграмма взаимной растворимости в системе вода − хлороформ − ацетон.

Ацетон

Хлороформ

Вода

Т

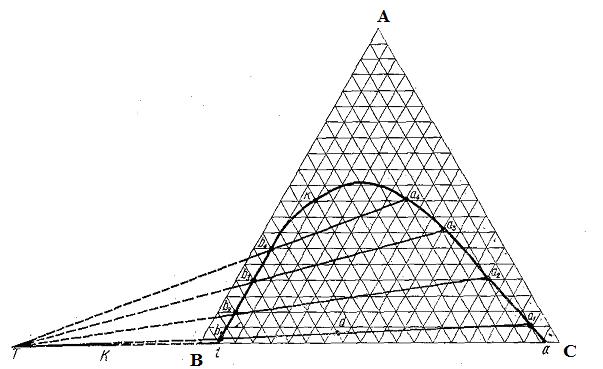
Рис. 3.14. Диаграмма взаимной растворимости в системе вода – хлороформ – ацетон

Ацетон неограниченно смешивается как с водой, так и с хлороформом, тогда как хлороформ и вода практически нерастворимы друг в друге. Однако прибавление к смеси хлороформа с водой некоторого количества ацетона приводит к увеличению взаимной растворимости первых двух фаз (хлороформа и воды).

При определенном содержании ацетона, зависящем от соотношения количеств воды и хлороформа, система становится гомогенной. Таким образом, диаграмма растворимости оказывается разделённой бинодальной кривой (рис. 3.14) на гетерогенную область, лежащую под этой кривой, и гомогенную область, расположенную над ней. Составы двух жидких фаз, на которые распадается система, отвечающая любой фигуративной точке в гетерогенной области (например, точка о на рис. 3.14), могут быть определены только опытным путем. Это объясняется тем, что в данном случае невозможно графически найти положение конноды, так как вся плоскость треугольника характеризуется постоянством температуры и давления. Составы двух сопряжённых слоёв (фаз, находящихся в равновесии) представляют собой насыщенные растворы хлороформа в водном слое (левая ветвь бинодальной кривой) и насыщенные растворы воды в хлороформе (правая ветвь бинодальной кривой) в зависимости от содержания ацетона. К треугольной диаграмме (как и к диаграмме бинарных систем) применимо правило рычага. Массы сопряжённых слоев (g_a и g_b) обратно пропорциональны расстояниям от фигуративной точки системы o до точек составов этих слоёв, a и b (рис. 3.14):

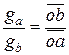
Если добавить к рассматриваемой системе новые порции ацетона, он будет неравномерно распределяться между двумя слоями. Поэтому на диаграмме наклон коннод (рис. 3.14) будет изменяться (в данном случае – возрастать).

В соответствии с приближённым правилом Тарасенкова продолжения всех коннод пересекаются в одной точке Т, лежащей на продолжении одной из сторон треугольника, а касательная, проведённая из этой точки к бинодальной кривой, определяет положение критической точки смешения К. Это правило позволяет по одной экспериментально определенной конноде найти положение точки Т и, проведя лучи из этой точки до пересечения с бинодальной кривой, оценить составы сопряжённых слоёв при других заданных валовых составах системы.

Работа 3.8. Построение изотермы взаимной растворимости в трёхкомпонентной жидкой системе

Цель работы. Построить диаграмму растворимости в трёхкомпонентной системе.

Методика выполнения работы. Взаимную растворимость в трёхкомпонентной системе обычно определяют методом титрования и анализа сопряжённых растворов. Этот метод заключается в том, что, приготовив ряд двухкомпонентных смесей различного состава, поочередно титруют их третьим компонентом. При этом возможно два варианта:

1. Исходная смесь представляет собой гомогенную систему (например, бензол – ацетон). Возникновение устойчивого помутнения при добавлении по каплям третьего компонента (воды) указывает на насыщение раствора третьим компонентом и появление следов второй фазы. Фигуративная точка полученной трёхкомпонентной смеси будет лежать на линии, соединяющей точку исходной бинарной смеси (бензол – ацетон) с вершиной треугольника (100 % воды). Аналогичным титрованием смесей с различными соотношениями бензол:ацетон можно получить целый ряд точек, лежащих на бинодальной кривой.

2. Исходная смесь представляет собой гетерогенную систему (например, бензол – вода). При добавлении по каплям третьего компонента (ацетона) вначале мутная двухфазная смесь становится прозрачным раствором. Момент исчезновения второй фазы отвечает достижению состава трёхкомпонентного раствора, фигуративная точка которого лежит на бинодальной кривой. В этом случае фигуративная точка полученной трёхкомпонентной смеси будет лежать на линии, соединяющей точку исходной бинарной смеси (бензол – вода) с вершиной треугольника (100 % ацетона).

Оба варианта дают одинаковые результаты, поскольку положение равновесия не зависит от того, с какой стороны к нему приближается система.

Последовательность выполнения работы. Исходные бинарные смеси в количестве 5 мл каждая готовят в конических колбочках с притертыми пробками. Рекомендуются следующие объёмные соотношения компонентов: 1:9; 2:8; 3:7; 4:6; 5:5; 6:4; 7:3; 8:2; 9:1. К каждой бинарной смеси приливают по каплям из бюретки третий компонент. По варианту 1 титрование ведут до появления устойчивого помутнения смеси. По варианту 2 титрование ведут до исчезновения мути и возникновения прозрачного раствора.

Количество третьего компонента х (см³), пошедшее на титрование, пересчитывают в объёмные проценты по формуле:

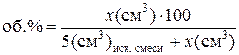
Для нанесения на треугольной диаграмме точек, соответствующих составам полученных тройных систем, объёмные проценты третьего компонента откладывают на линиях, соединяющих точки составов исходных двойных систем с вершиной треугольника, отвечающей 100 % третьего компонента. Соединив нанесённые точки плавной кривой, получают изотерму растворимости в данной трехкомпонентной системе (рис. 3.14).

Метод титрования позволяет быстро и точно построить изотерму растворимости в системе трёх жидкостей, но не даёт возможности установить положение коннод и составы сопряжённых слоёв.

Дата добавления: 2017-02-01