
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обработка результатов экспериментов
|
|
|
|
1. 1. Строят графики зависимости давления насыщенного пара от температуры в координатах p − t и 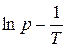 .
.
2. Из графика 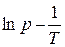 определяют коэффициенты А и В эмпирического уравнения (3.4).
определяют коэффициенты А и В эмпирического уравнения (3.4).
2. Определяют нормальную температуру кипения жидкости (при 760 мм рт. ст.).
3. Из коэффициента В вычисляют теплоту испарения жидкости:
Δисп Н = − R·B.
4. По уравнению (3.5) рассчитывают теплоту испарения жидкости для трех интервалов температур (по указанию преподавателя).
5. Вычисляют истинную теплоту испарения жидкости по графику p − t для температуры, указанной преподавателем.
6. Рассчитывают изменение энтропии испарения при нормальной температуре кипения по уравнению (3.6).
Контрольные вопросы
1. Какой пар называют насыщенным?
2. Что называют температурой кипения?
3. Как зависит температура кипения от давления?
4. Какие допущения следует принять, чтобы проинтегрировать уравнение Клапейрона–Клаузиуса?
5. Как выглядит график и уравнение для расчёта средней теплоты испарения в заданном интервале температур?
6. Как выглядит график и уравнение для расчёта истинной теплоты испарения при заданной температуре?
3.3. Фазовые равновесия в двухкомпонентных системах
3.3.1. Общие представления о растворах
В уравнениях состояния двухкомпонентных систем число переменных равно четырём: T, p, c 1, c 2. Построение диаграмм в четырехмерном пространстве невозможно, и это вынуждает прибегать к некоторым упрощениям. При выражении концентрации в мольных долях мольная доля второго компонента уже не может быть независимой величиной, она равна Х 2 = 1 – Х 1. В этом случае получается трёхмерная объёмная диаграмма. В практической повседневной работе пользуются ещё более упрощенными диаграммами, а именно сечениями объёмной диаграммы плоскостями, отвечающими постоянному давлению или постоянной температуре.
Наиболее важным понятием для двухкомпонентных систем являются растворы. Растворы - однофазные смеси двух или более веществ, которые в термодинамике принято называть компонентами раствора. Помимо давления и температуры свойства растворов зависят от соотношения между количествами компонентов, т.е. от концентрации компонентов. В термодинамике наиболее удобно выражать концентрацию в мольных долях – Xi. Мольная доля компонента – отношение числа молей данного компонента к сумме чисел молей всех компонентов в растворе.
Цель термодинамической теории растворов состоит в том, чтобы связать различные свойства раствора и найти способы предсказания свойств растворов исходя из свойств чистых компонентов. В общем случае это невозможно, поскольку при образовании растворов происходят различные физические и химические взаимодействия молекул компонентов. Поэтому свойства растворов не являются простой суммой свойств компонентов. Вещество, переходя в раствор, теряет свою индивидуальность. Однако в частном случае, когда взаимодействие между одноименными и разноименными молекулами в растворе одинаково (все молекулы обладают одинаковыми силовыми полями), образуются так называемые идеальные растворы. Для них характерна аддитивность экстенсивных свойств компонентов. Общее давление пара над раствором складывается из парциальных давлений компонентов, которые определяются по закону Рауля:
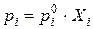 , (3.7)
, (3.7)
где 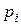 – парциальное давление i -го компонента над раствором,
– парциальное давление i -го компонента над раствором, 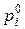 – давление насыщенного пара i -го компонента,
– давление насыщенного пара i -го компонента, 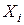 – мольная для i -го компонента.
– мольная для i -го компонента.
Любые отклонения от закона Рауля означают образование неидеальных растворов, для расчёта свойств которых используют метод парциальных мольных величин.
Если экстенсивное свойство раствора L зависит в общем виде от давления, температуры и состава, L = f (p, T, ni), то частную производную этого свойства по числу молей данного компонента при постоянстве давления, температуры и чисел молей остальных компонентов называют парциальной мольной величиной этого компонента:
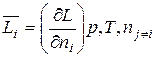 (3.8)
(3.8)
С помощью парциальных мольных величин всех компонентов можно рассчитать общее экстенсивное свойство раствора данного состава:
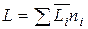 (3.9)
(3.9)
Это уравнение является выражением свойства аддитивности парциальных мольных величин и аналогично простой аддитивности мольных величин в случае образования идеальных растворов. Изменения парциальных мольных величин с изменением состава раствора связывает уравнение Гиббса–Дюгема:
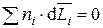 , (3.10)
, (3.10)
которое используется для определения зависимости парциальной мольной величины одного компонента, если эта зависимость известна для другого компонента.
3.3.2. Химический потенциал и активность компонента
в растворе
Химический потенциал компонента в растворе 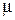 i представляет собой парциальную мольную энергию Гиббса. Для идеального газа химический потенциал зависит от давления:
i представляет собой парциальную мольную энергию Гиббса. Для идеального газа химический потенциал зависит от давления:
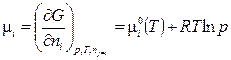 (3.11)
(3.11)
Химический потенциал данного компонента в смеси идеальных газов аналогично связан с его парциальным давлением:
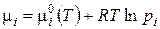 (3.12)
(3.12)
Рассмотрим теперь чистую жидкость, находящуюся в равновесии со своим паром. Так как химические потенциалы компонентов в равновесных фазах равны, уравнение (3.11) имеет силу и для жидкости:
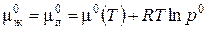 (3.13)
(3.13)
Для химического потенциала компонента в жидкой смеси, пар над которой подчиняется уравнению идеальных газов, аналогично уравнению (3.12) имеем:
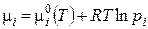 (3.14)
(3.14)
Из уравнений (3.13) и (3.14) легко получить
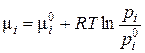 (3.15)
(3.15)
Для идеальных растворов при всех концентрациях выполняется закон Рауля (3.7). Тогда для компонента идеального раствора химический потенциал можно выразить через мольную долю
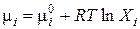 (3.16)
(3.16)
В реальных растворах отношение  не равно мольной доле жидкого компонента. Оно характеризует положительные или отрицательные отклонения от закона Рауля и называется термодинамической активностью компонента ai. Таким образом, если пар над раствором можно считать идеальным газом, активность компонента в растворе:
не равно мольной доле жидкого компонента. Оно характеризует положительные или отрицательные отклонения от закона Рауля и называется термодинамической активностью компонента ai. Таким образом, если пар над раствором можно считать идеальным газом, активность компонента в растворе:
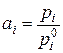
Введя это обозначение, получим следующее выражение для химического потенциала:
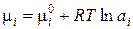 (3.17)
(3.17)
Мерой отклонения свойств данного раствора от свойств идеального раствора той же концентрации является отношение
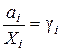 ,
,
которое носит название коэффициента активности. С учётом уравнений (3.16) и (3.17) разность химических потенциалов компонента в неидеальном и идеальном растворе представляет собой величину максимальной полезной работы перенесения 1 моля данного компонента из идеального раствора в реальный раствор той же концентрации:
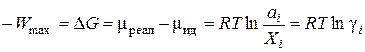 (3.18)
(3.18)
Как видно из полученного выражения, работа W max зависит от коэффициента активности.
Поскольку величина 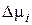 представляет разность между химическими потенциалами компонента в растворе с данной концентрацией и в стандартном состоянии, она называется относительным химическим потенциалом.
представляет разность между химическими потенциалами компонента в растворе с данной концентрацией и в стандартном состоянии, она называется относительным химическим потенциалом.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 67; Нарушение авторских прав?; Мы поможем в написании вашей работы!