Часть 7. Линейное программирование 2 страница

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где 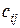– цена перевозки единицы груза из пункта в пункт .

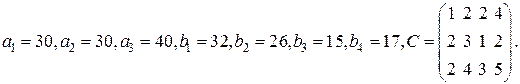
6. Найдите решение матричной игры с матрицей .

Вариант 13

1. Составьте математическую модель задачи.

Хозяйство располагает следующими ресурсами: площадь – 100 единиц, труд – 120 единиц, тяга – 80 единиц. Хозяйство производит четыре вида продукции: П₁, П₂, П₃, П₄. Затраты на производство единицы каждого вида продукции и доход от их производства указаны в таблице:

Продукция	Затраты на ед. продукции	Доход
площадь	труд	тяга
П1
П2
П3
П4

Организовать производство так, чтобы получить максимальный доход.

2. Решите графически задачу: найдите экстремумы функции , если , .

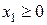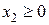3. Дана задача линейного программирования

,

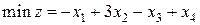а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

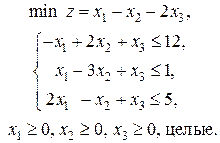
5. Решите методом потенциалов транспортную задачу, где 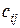– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Вариант 14

1. Составьте математическую модель задачи.

Производятся изделия А и В, при изготовлении которых используются два типа технологического оборудования α и β. На производство единицы изделия А оборудование α используют 2 ч, а β – 1 ч. На производство единицы изделия В оборудование α используют 1 ч, а β – 2 ч. Администрация на изготовление изделий может выделить оборудование α на 10 ч, а оборудование β – на 8 ч.

Спланировать производство изделий А и В так, чтобы общая прибыль была наибольшая, если от реализации единицы изделия А прибыль равна 5 руб., В – 2 руб.

2. Решите графически задачу: найдите экстремумы функции , если , .

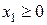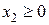3. Дана задача линейного программирования

,

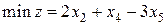а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

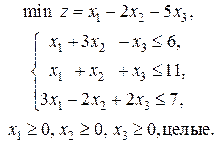
5. Решите методом потенциалов транспортную задачу, где 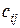– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Вариант 15

1. Для производства двух видов сплавов используют в качестве добавок редкие металлы. Их запасы, нормы расхода на 1 т каждого сплава и прибыль от реализации 1 т каждого сплава приведены в таблице.

Вид сплава	Содержание добавок в 1 т сплава (кг)	Прибыль от реализации 1 т сплава (тыс. руб.)
титан	молибден	хром
I
II
Запасы металлов (кг)

Составить план выпуска сплавов, который дает максимальную прибыль.

2. Решите графически задачу: найдите экстремумы функции , если , .

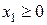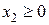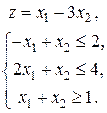
3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где 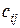– цена перевозки единицы груза из пункта в пункт .

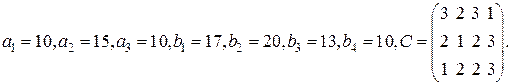
6. Найдите решение матричной игры с матрицей .

Вариант 16

1. Составьте математическую модель задачи.

Цех выпускает трансформаторы двух видов. На один трансформатор 1-го вида расходуется 5 кг трансформаторного железа и 3 кг проволоки, а на один трансформатор 2-го вида – 3 кг железа и 2 кг проволоки. От реализации одного трансформатора 1-го вида цех получает прибыль 12 000 руб., а 2-го вида – 10 000 руб. Сколько трансформаторов, и какого вида должен выпустить цех, чтобы получить наибольшую прибыль, если цех располагает 480 кг железа и 300 кг проволоки?

2. Решите графически задачу: найдите экстремумы функции , если , .

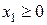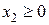3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

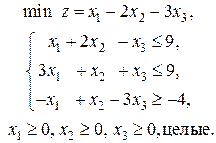
5. Решите методом потенциалов транспортную задачу, где 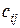– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Вариант 17

1. Составьте математическую модель задачи.

Совхоз отвел три земельных массива размерами в 5 000, 8 000, 9 000 га под посевы ржи, пшеницы и кукурузы. Средняя урожайность (в ц на 1 га) по массивам указана в таблице:

	Массивы
I	II	III
Рожь
Пшеница
Кукуруза

За 1 ц ржи совхоз получает 20 т.руб., за 1 ц пшеницы – 25 т.руб., за 1 ц кукурузы – 14 т.руб. Сколько гектаров и на каких массивах совхоз должен отвести под каждую культуру, чтобы получить максимальную выручку, если по плану он обязан сдать не менее 1 900 т ржи, 15 800 т пшеницы и 30 000 т кукурузы?

2. Решите графически задачу: найдите экстремумы функции , если , .

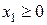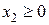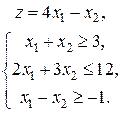
3. Дана задача линейного программирования

,

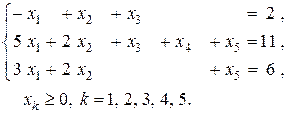
а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где 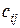– цена перевозки единицы груза из пункта в пункт .

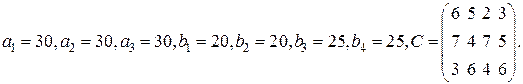
6. Найдите решение матричной игры с матрицей .

Вариант 18

1. Составьте математическую модель задачи.

Для нарезки заготовок длиной 20, 25 и 30 см используются прутки длиной 75 см. Требуется за смену нарезать следующее количество заготовок: длиной 20 см – 300 шт., 25 см – 270 шт., 30 см – 350 шт. Из одного прутка можно нарезать заготовки различной длины. Требуется определить, какое количество прутков необходимо разрезать каждым из возможных вариантов, чтобы число заготовок соответствовало заданной программе, и чтобы при этом общая длина всех концевых остатков была минимальной?

2. Решите графически задачу: найдите экстремумы функции , если , .

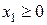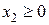3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где 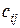– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Вариант 19

1. Составьте математическую модель задачи.

В обработку поступили две партии досок для изготовления комплектов из трех деталей, причем первая партия содержит 50 досок длиной по 6,5 м каждая, вторая содержит 200 досок длиной по 4 м каждая. Комплект состоит из двух деталей по 2 м каждая и одной детали длиной 1,5 м. Как распилить все доски, чтобы получить наибольшее число комплектов?

2. Решите графически задачу: найдите экстремумы функции , если , .

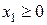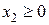3. Дана задача линейного программирования

,

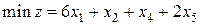а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где 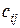– цена перевозки единицы груза из пункта в пункт .

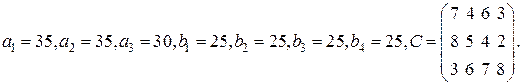
6. Найдите решение матричной игры с матрицей .

Вариант 20

1. Составьте математическую модель задачи.

Фирма производит одежду для охотников, туристов и охранных структур. Дополнительно фирма решила изготавливать шапки и подстежки из натурального меха. Затраты на производство этих изделий и запасы сырья представлены в таблице. Спрос на шапки составляет не более 600 шт. в месяц, а подстежек – не более 400 шт. в месяц.

Сырье	Расход сырья на производство, дм	Средний запас в месяц, дм
шапки	подстежки
Мех			61 600
Ткань	1,5		15 000
Оптовая цена, руб./шт.

Определить объемы производства этих изделий, обеспечивающих максимальный доход от продажи.

2. Решите графически задачу: найдите экстремумы функции , если , .

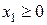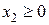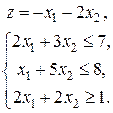
3. Дана задача линейного программирования

,

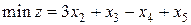а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

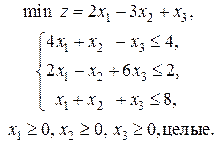
5. Решите методом потенциалов транспортную задачу, где 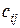– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Вариант 21

1. Составьте математическую модель задачи.

Имеется два станка, на которых могут обрабатываться детали трёх видов. Количество деталей каждого вида, обрабатываемых на каждом станке в течение рабочего дня, приведено в таблице.

Станки	Детали вида

Полный комплект состоит из двух деталей первого вида, одной детали второго вида и четырёх деталей третьего вида. Какую часть рабочего дня каждый станок должен обрабатывать детали каждого вида с тем, чтобы число комплектов деталей было наибольшим?

2. Решите графически задачу: найдите экстремумы функции , если , .

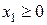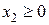3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

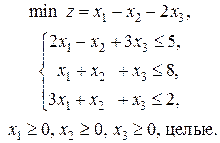
5. Решите методом потенциалов транспортную задачу, где 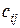– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .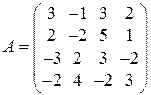

Вариант 22

1. Составьте математическую модель задачи.

Имеются три экскаватора разных марок. С их помощью нужно выполнить три вида земляных работ объёмом в 20 000 м³ каждый. Время работы экскаваторов одинаково, производительность в м³/ч по каждому виду работ приведено в таблице.

Экскаватор	Вид работ
А	В	С

Распределить время работы каждого экскаватора так, чтобы задание было выполнено в кратчайший срок.

2. Решите графически задачу: найдите экстремумы функции , если , .

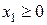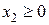3. Дана задача линейного программирования

,

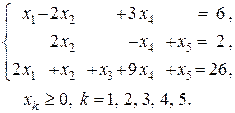
а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

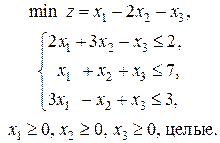
5. Решите методом потенциалов транспортную задачу, где 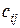– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Вариант 23

1. Составьте математическую модель задачи.

Планируется установление договорных связей между тремя совхозами и тремя торговыми предприятиями по поставке овощей. Заказы торговых предприятий на плановый период и возможности поставщиков, а также расстояния (в км) приведены в таблице.

Предложение, т	Спрос, т
В1=200	В2=140	В3=60
А1=160
А2=150
А3=90

Определить схему связей, соответствующую минимальному грузообороту.

2. Решите графически задачу: найдите экстремумы функции , если , .

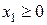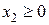3. Дана задача линейного программирования

,

а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где 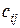– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Вариант 24

1. Составьте математическую модель задачи.

Предприятие по переработке лесоматериалов выпускает пиломатериалы и фанеру. Для изготовления 8 м³ пиломатериалов расходуется 6 м³ еловых и 13 м³ пихтовых лесоматериалов. Для производства 100 м³ фанеры расходуется 6 м³ еловых и 10 м³ пихтовых лесоматериалов. Общие запасы сырья – 80 м³ еловых и 200 м³ пихтовых лесоматериалов. В соответствии с плановым заданием предприятие должно изготовить не менее 10 м³ пиломатериалов и 1 100 м³ фанеры. Прибыль, получаемая от реализации 1 м³ пиломатериалов – 12 руб., а при реализации 100 м³ фанеры – 50 руб. Составить план производства, максимизирующий прибыль.

2. Решите графически задачу: найдите экстремумы функции , если , .

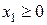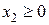3. Дана задача линейного программирования

,

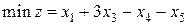а) Найдите все базисные решения системы ограничений. Выберите из них допустимые.

б) Решите данную задачу графически.

в) Решите данную задачу методом искусственного базиса.

4. Решите задачу линейного программирования

5. Решите методом потенциалов транспортную задачу, где 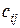– цена перевозки единицы груза из пункта в пункт .

6. Найдите решение матричной игры с матрицей .

Дата добавления: 2017-02-01