Лекция Ферми энергиясы. Ферми беті. 2 страница

-

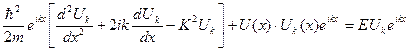
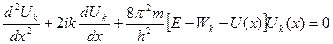(7)

Мұндағы (7а)

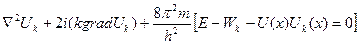(7б)

1. 0<х<а облысында U=0 (7) теңдеудің шешімі:

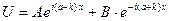
Мұндағы 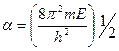(8)

2. а<х<а+в облысында U≠0 және Е<U (барлық биіктігі электронның кинетикалық энергетикасы жоғары (көп))

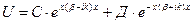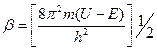; (9)

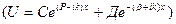
А,В,С,Д тұрақтылары, U функциясы және оның 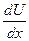туындының потенциалыдарын яғни х=0 және х=а нүктесінде үздікссіз болатынын етіп таңдап алынды. Нүктелерде сонымен бірге U(х) функциясының периодын болу керектігі туралы талапқа сай оның мәні х=а болатын мәні х=-в мәніне тең болуы тиіс.

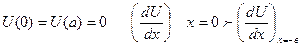
Осы шарттарды қолданып, төрт сызықты және біртекті теңдеулер аламыз:

А+В=С+Д

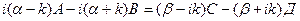
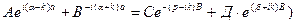(10)

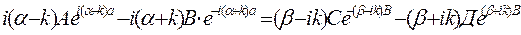
Егер теңдеулер жүйесіндегі белгісіз шамалар алуға коэффициент құралған детерминді нөлге тең болса, онда мұндай теңдеулердің құралатын, нөлге тең емес шешімі болады.

Мақсаты: кристалдағы электронның энергиялық спектрінің сипатын (көрсету) және оның күйін анықтайтын толқындық функциясының түрін көрсету.

Металдардың (қатты денелердің) қазіргі кванттық теориясында ұжымдалған электрондар (коллектированные электрон) кристалдық тордың периодты күш өрісінде қозғалады (болады) деп есептеледі. Сонымен бірге әрбір электронға, басқа қосған барлық электрондар тудыратын өріс әсер етеді.

Кристалдың кейбір көлеміндегі айының 1см³ көлеміндегі атомдардың санын N деп белгілесек, онда талдау жасалынып отырған жүйе кристалдық тордың түйіндерінде орналасқан N геон туады. Және Nν электрондардан туады, мұндағы ν – металдардың валенттілігі.

Иондардың ішкі қабықшаларындағы электрондар ядролармен тығыз байланысқан (мықты байланысқан), сынуын кристалл – ені тұратын жүйе болып табылады: ауыр жүйе (қисықтарының түйініндегі иондар) және жеңіл жүйе (валентті электрондар немесе ұжымдалған электрондар)

Көлемі 1см³ зат ішінде 10²³ жуық жуықтаулар болады. () Ендеше, қарастырылып отырған жүйе үшін Шредингер теңдеуінің дәл шешімін табу мүмкін емес.

Бірақ, кейбір қарапайым (ықшамдау) жорамасын жасап, қатты дененің электрондық теориясының негізгі физикасының нәтижелерін алуға болады.

Біріншіден, құрамында ядро болатындықтан, әрбір ионның массасы, (кез келген) әрбір электрон массасынан көп үлкен. Онда бірінші жуық тура иондар қозғалмасты деп қаратыруға болады.

Сонымен бірге, талдаудың 1 – ші сатысында (этапында) әрбір нейтрон басқа электрондарға тәуелсіз, тор түйіндерінде орналасқан иондар тудыратын (кейбір) (эффектісін күш өрісінде) (қозғалады деп, (қарастырылады және қарастырып отырған электронның басқа электрондардың тудыратын кейбір эффектісінің күш тудыратын өрісінде қозғалады деп қарастырылады.

Электрондар иондар арасындағы кеңістікте біртекті орналасатындықтан, олардың ортасында өрісі иондар арасындағы барлық кеңістікте тұрақты. Сондықтан қарастыратын эффектісін өріс, кристалдық тордың күш өрісі сияқты, кеңістікте периодты болады.

Сонымен толқындардың 1 – ші сатысында, бір электрон периоды кристалл торының периодына тең күш өрісінде қозғалады деп қарастырамыз. Ббасқа қалған электрондар қарастырылып отырған электронның қозғалыс заңдылықтарына бір электронды жуықтау деп аталады.

Осы жуықтауда, кристалдағы электрон үшін Шредингер теңдеуін жазамыз:

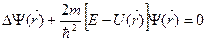(1)

(1) теңдеудегі Ψ(ŕ) – электронның іздеп тордың толқындық функциясы,

Е – кристалдағы электрон энергиясы.

U(ŕ) – электрон қозғалатын периодты өрістегі, электронның потенциалдық энергиясы

Периодты функцияның 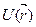мәні кристалл ішіндегі, ара қашықтықтары бір – бірінен, түзу тордың әртүрлі векторлары болып табылатын кесінділер нүктелерде бірдей.

(Кесінділер – түзу тордың әртүрлі векторлары).(Тордың векторы деп, жолын түрде, R векторын айтамыз). Толрдың векторын, жолын түрде, 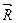деп белгілейміз.

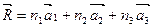(2)

Нда кристалдағы электрон қозғалатын потенциалдық өрістің периодтың қасиетін лентозый қатынаспен өрнектеледі:

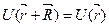(3

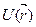- тәуелділігінің ашық түрі осы уақытқа дейін белгісіз, бірақ, 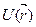- уі (3) формула түріндегі периодты функция деп, бірқатар маңызды қорытындылар (нәтижелер) алуға болады.

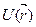функциясын, кері тор кеңістігінде, фурье қатарына жіктелу түрінде жазайық:

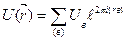(3а) _і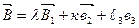

(3а) формуласы үш өлшем үшін жалпыланған мынандай қатынас болып табылады.

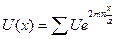- бұл периоды а – ға тең, периодты функция U(х) тең Фурье қатарына жіктелуі болып табылады.

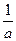- кері тордың базистік есептерін.

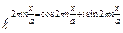(комплекс сандар үшін Эйлер формуласы: )

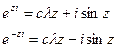Сапамен, кристалл ішіндегі электрон үшін Шредингер теңдеуінің түрі мынадай:

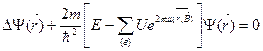(1а)

Шредингер (1) теңдеуіне талдау жасау, қатты дененің қазіргі электрондық теориясының қорытындылары шығатын, скуидаментальді нәтижеге әкеледі.

Мұндай нәтиже, Блох теоремасы деп аталатын атпен белгілі:

Блох теремасы мына түрде айтылады:

Периодты потенциалдағы толқындық теңдеудің меншікті функциялары, жазық толқынның функциясының 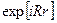кристалдық тордағы периодты функция болып табылады.

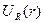функциясының көбейтіндісіне тең:

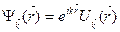(4)

Мұндағы 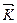- модулы кері ұзындық өлшемін өлшем вектор.

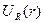- периоды тор периодына тең, кейбір функция. (3)

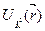функциясын модуляцияланатын функциясын оқиды.

(4)формуламен анықталатын кристалдағы электронның толқындық функциясы Блохтың дтолқындық функциясы деп аталады немесе Блох толқыны деп те аталады. Ол жазық толқын болып табылады.

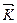- кристалдың электрондық толқын векторы.

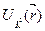- периоды тор периодына тең, кейбір функция

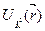- фундамент модуляцияланатын функцияланады.

(4) формуламен анықталады. Блохтың теоремасы функциясы деп аталады. Немесе Блох толқыны деп аталады. Ол жазық толқын болып табылады.

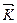- кристалды электронның толқын векторы.

Металдағы өткізгіштік электрондар саны N электрондармен толықтырылған энергиялық күйдің 2 есесіне тең:

N=2 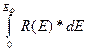(4.13)

(3.23.)өрнекті пайдалана отырып R(E)dE,мынаны аламыз:

(4.14.)

(4.14.)өрнектен металдағы еркін электрондардың концентрациясын мына түрде жазамыз:

N= 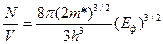(4.15.)

Соңында Ферми энергиясы үшін мынаны табамыз

E_ф= 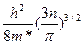(4.16.)

Өзіміз күткендегідей,Ферми энергиясы металдағы өткізгіштік электрондардың концентрациясына тәуельді.

Металдағы өткізгіштік электрондардың орташа E энергиясын температурасы ОК кезінде табамыз,егер ондағы барлық электрондардың энергиясының қосындысын,

E= (4.17.)

Электрондардың санына,яғни (4.14.)өрнекке бөлеміз:

E= 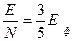(4.18.)

Мысал ретінде мыс үшін Ферми энергиясының мәнін есептейміз.Әрбір мыс атомы бір өткізгіш электрон деп және m≈m деп есептейміз.Мыстағы еркін электрондардың концентрациясы мыстағы атомдардың концентрациясына тең,ол мынаған тең:

n=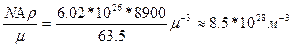

Бұл жерде N-Авогадро саны, ρ-мыстың тығыздығы және μ- мыстың килограм-атомдық салмағы.

Алынған қорытындыны (4.16.)өрнекке қойып,мынаны аламыз:

Мыстың өткізгіштік электрондарының орташа энергиясы (4.18.)формула бойынша шамамен 4,2 эв-қа тең.

Өткен тараудағы (9)қарастырылған рентгендік спектральдік жолақты ескеретін болсақ,онда бұл жолақтағы фотонның максимал және минимал энергиясының арасындағы айырмашылық осы металл үүшін Ферми энергиясының өлшемін береді.4.1.кестеде кейбір металдар үшін Ферми энергиясының мәнедері және электрондық газдар туындайтын температуралары жазылған.

метал	Еф*эв	Тф,К	метал	Еф*эв	Тф,К
Cs K Na Li	1.53 2.14 3.12 4.72		Ag Al Be	5.5 11.9 14.6

Өткізгіштік электрондарын тарату туралы алынған ұсыныстар, металдарда олардың температурасының өзгеруіндегі бағытын түсіндіруге мүмкіндік береді.Энергетикалық зонада металдар мүлде жоқ болғандықтан барлық деңгейлер бірнеше электронвольттардың энергиясының деғгейіне шейін бос емес, ал кристалдық тордың жылулық тербелісінің энергиясы электрнвольттардың бірнеше жүздеген қашықтықтарының көлемін құрайды,онда металдың температурасы жоғарылаған кезде электрндардың тек қана мағынасыз бөлшектері,тордың жылулық тербелісінен қосымша энергия ала отырып, жоғары энергетикалық деңгейге өте алады.Мұны деңгейлердің бос шамасы КТ мөлшерімен анықталуын және Е_ф энергиясының КТ мөлшеріменреттелуін деңгейде орналасқан электрондар көрсетеді.

Осылайша, температураның металдағы электрндардың таралуына ықпал етуі,Ферми деңгейіне жақын энергетикалық деңгейде орналасқан электрон энергиясының өзгеруіне алып келеді.

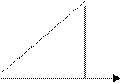
4.3 – суретте

N(E)

0 E

E_ф

Энергия бойынша мүлдем жоқ болған кездегі (тұтас сызық) және Т>О^о К температурадағы электрондардың таралуы графикалық түрде көрсетілген.

Ферми деңгейіне жақын электрон таралуының өзгерісін рентгендік спектр көмегімен қадағалауға болады.4.4 – суретінен температура жоғарылағандағымагнидің спектрлік сызық шегінің кеңейтілуі көрініп тұр.Ферми деңгейінің тұрған жері суретте осы қисық сызықтардың әр қайссының ортасына сейкес келеді.4.4- суретінде көрініп тұрғандай, металдағы электрон бөлігінің температурасы көтерілгенде тордың жылулық тербелісінен энергия ала отырып Ферми деңгейіне төмен орналасқандығын және фотонның үлкен максимал энергиясының төменгі температурада фотонның энергияларымен сәулеленуіне әсер етеді.

Біз электрондық газдардың қасиеттері металда классикалық идеалдық газдың қасиетінен принпринципті ерекшеленіп тұрғанын көріп тұрмыз.Электрондық газды металда солғын деп атайды.Газдың солғындауының ең басты белгісі оның бір бөлігінің энергиялары температурадан тәуелсіздігі.

Кез-келген электрон кристалдықтары бар энергиямен ауыса алмайынша, электрндық газ металда солғын болып қалады,ал бұл өз кезегінде тек қана тордың жылулық тер белісінде КТ орташа энергиясы Ферми энергиясыннан аз болмаған кезде ғана мүмкін болады.,яғни

КТ≥E_ф

Температура

Т_ф= 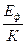(4.18)

Газ солғын емес күйден солғын күйге өтетін төмен температура, солғын температура немесе фермилік температура деп аталады.4.1 Кестеде металлдар қатары үшін фермилік температура мағынасы келтірілген. Берілген кестеден көріп тұрғандай, металдағы электрондық газ барлық мүмкін температурада солғын күйде қалады.

Қатал талқылағанда, Ферми энергиясы температураның бойымен өгеретінін көруге болады.Соның ішінде, Ферми энергиясы температураның жоғарылауымен азаяды, ал электрондардың орташа энергиясы өседі.Бірақ бұл өзгерістер әдеттегі температурада алдағы уақытта біз оны еске алатындай, соншалықты үлкен емес.Температура жоғарылағандағы Ферми энергиясының азаюын былай түсіндіруге болады:Ферми деңгейінен төмен энергетикалық деңгейде орналасқан Т>О⁰К температурадағы электрондар бөлігі, бастапқы деңгейінен бос қалдырып, жоғары деңгейге өтті.Бос деңгейлер төмен деңгейлі электрондар мен толығуы мүмкін.Энергетикалық деңгейдегі температураның жоғарылауының нәтижесінде, Ферми деңгейінің жартысына тең толықтыру ықтималдылығы, төмен түседі.

9-лекция. Аумақтардың электрондармен толуы.

Металдардың классикаалық теориясы негізінде бос электрондардан тұратын электронды газ ұғымы жатыр.Электронды газға бір атомды идеал газдың қасиеті сәйкес келеді.Бос электрондар тоқтаусыз және ретсіз қозғалып олардың орташа кинетикалық энергия қозғалысы 3/2 RT тең.Олар соқтығысу кезінде кристал торлармен энергия алмасады.Сырттан иәсер еткен электр өрісі әсерінен металда бос электрондар қозғалысы пайда болады. Электрондар екі соқтағысу арасында қозғалысы үдейді.Электр соқтығысу барысында пайда болған энергияны криссталға береді.Осы айтылғандар негізінде металдардың кейбір қасиеттерін түсіндіруге болады.

Келесі екі соқтығысу арасында электр өрісінің әсерінен электрондар мына формула бойынша қозғалады.

a=

Соқтығысу алдындағы электронның алатын ең жоғарғы жылдамдығы мынаған тең.

V_макс =α τ

Бұл жердегі - электрондардың бос қозғалысқа кеткен орташа уақыты.

Электронның орташа қозғалысы V аксималды жылдамдықтың жартысына тең. Яғни, электронның соқтығыстан кейінгі жылдамдығы 0-ге тең болып одан әрі оның жылдамдығы сызықты түрде өседі.

V= 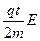(4.1)

4.1. –гі мәнді алып ток тығыздығына қойып

δ= q_e n v,

былай қорытамыз

δ= 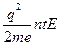(4.2)

Өткізгіш бойындағы ток тығыздығы ондағы электр өрісінің кернеуіне тура пропорционал,бұл дегеніміз Ом заңының негізі. Осыдан келіп тәжірибе жүзінде табылған заңды шығарып аламыз.

γ= 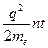(4.3)

(4.3) формуласы металдың меншікті электр өткізгіштігін сипаттайды.Егерде, электрондердың қарапайым қозғалысы жылулық қозғалысына қарағанда айтарлықтай аз екенін ескерсек онда электронның еркін қозғалысы былай анықталады. τ= 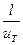(4.4)

Бұл жерде τ- электронның еркін қозғалысының орташа ұзындығы, U_T- электронның жылулық қозғалыс кезіндегі орташа жылдамдығы классикалық электрон теориясындағы L – кристалдағы атомдар арасындағы арақашықтыққа теңейді. (4.4) формуланың мәнін (4,3)-ке қоямыз

γ= 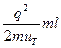(4.5)

Осы формуланы анықталған деп айтуға болмайды.Себебі жекеше алған электронның орташа қозғалысын қарастырып отырмыз.Ал шыққан нәтижені барлық бос электрондар үшін пайдаланамыз.Ең дұрысы электр өрісінің барлық бос электрондар жиынына әсерін қарастыру керек.Мұнда олардың жалпы импульсы өріс және электрондардың кристал торымен соқтығысуынан өзгеріп отырады.Мұндай қарастыру электрондардың орташа құйынды қозғалысының жылдамдығы біздің алғанымыздан екі есе көп болып шығады. Яғни (4,5) формуласы мынадай сипатқа ие болады.

γ= 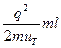(4.6)

Көріп отырғанымыздай металлдың меншікті электр өткізгіштігі метал табиғатына (n және l) және температураға (U_T  T +1/2)

Электрондық теорияның беретін тәуелдісі тәжірибеге сәйкес келмейді. (4,6) формулаға мәнді қойып, мына формуланы шығарамыз:

U_T = 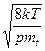(4.7)

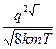γ= (4.8)

Осыдан келіп металлдың электр өткізгіштігі Т кері пропорционал өзгереді,сонымен қатар тәжірибеден белгілі болғанда металлдың электр өткізгіштігі Т-ға шамамен кері пропорционал өзгереді.(4,8) формуладағы металлдардың асқын өткізгіштік жағдайға өтуі абсолют 0- ден жоғары температурада өте жылдам (болатындығын) өтеді деуге болмайды.

Металдардың электрондық теориясынан тағы да бірнеше тәжірибелі заңдар шығаруға болады.Видеман – Франц заңын қарастырайық.Тәжірбие барысында ашылған заң былай дейді: Металдың жылу өткізгіштігі коэффициенті λ,оның меншікті электр өткізгіштігіне γ барлық металлдар үшін бірдей температурада бірдей екендігін көрсетеді.

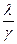=aT (4.9)

Бұл жерде а- тәжірибе барысында анықталатын коэффициент, ол металлдың табиғатына тәуелді емес. Егер металлдың жылу өткізгіштігі бос электрондар негізінде өтеді дейтін болсақ, онда металдың жылу өткізшіштік коэффициентін қабылдауымызға болады, оның формуласы:

λ= 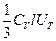(4.10)

Мұнда С_V - газдың жылу сыйымдылығын бірлігі L – бос электронның қозғалысының орташа ұзындығы,U_T - олардың орташа жылулық қозғалысы. 4.10 мәнін 4.5. мәнге бөле отырып 4.7, формуласына назар аударамыз және

С_V = nk

Осыдан келіп, 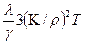аламыз (4.11)

Тәжірибе мәндері теориялық жағдайда алған мәнге сәйкес келеді.Осылайша электр теория Ом және Видеман – Франц заңдарын тәжірибе жүзінде дәлелдеп берді.Тура осындай жағдай Джоуль-Ленц заңын қорытқан кезде де шығады.Бірақ электрондық теория кейбір металдардың қасиеттерін түсіндірген кезде қайшылықтарға әкеледі.Бұған мысал ретінде атомның жылу сыйымдылық өлшемін айтуға болады.Электрондық теория бойынша металдың бос электрондары кристалл торлары мен соқтығысуы кезінде энергия алмасады.Сондықтан металлдың жылу сыйымдылығы С_м кристалл тордың жылу сыйымдылығы мен С_м және электронды газдың жылу сыйымдылығы қосындысына тұруы қажет.Кристалл торының жылу сыйымдылығы Дюлонг және Пти заңы бойынша

С_мкр =3 k ₀

Металдағы бос электронның саны атомдар санына сәйкес екендігін және электрондардың үш еркіндік сатысына сәйкес

С_МЭ= R₀ екендігін табамыз.

Атомдардың жылу сыйымдылығы мынаған тең болуы керек.

С_М = 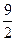R₀

Бос электрондары жоқ диэлектриктер үшін атомның жылу сыйымдылығы 3R₀ –ге. Бірақ тәжірибе көрсеткендей метал және диэлектриктер арасында атомдық жылу сыйымдылықтары бойынша айтарлықтай айырмашылық жоқ. Электрондар теориясы металдардың жылу сыйымдылығының температураға тәуелділігін дәлелдеп бере алмайды.Классикалық электрондар теориясының шектеулі екендігін оның бос электронды классикалық бөлшектер, ал олардың жиынтығын электронды газ оны классикалық идеалды газ ретінде қарастыруынан көруге болады.

Дата добавления: 2017-02-01