Приклад розв’язування задачі

Метод Гоморі

Короткі теоретичні відомості

Відведений час: 4 год.

Цілочислові задачі лінійного програмування

Мета: навчати студентів розв’язувати задачі цілочислового програмування за допомогою методу Гоморі та методу «віток та меж».

Завдання для практичного заняття:

1. Пригадайте основні теоретичні питання теми.

2. Орієнтовні запитання та завдання:

- у чому суть методу Гоморі;

- запишіть нерівність Гоморі;

- у чому суть методу «віток та меж»;

- запишіть нерівності «віток та між»;

3. Виконайте індивідуальне завдання.

Загальна задача цілочислового програмування записується так:

,

за умов

,

,

— цілі .

Даний метод був запропонований в 1958 році американським математиком Р. Гоморі спочатку для повністю цілочислових задач лінійного програмування, а пізніше і для частково цілочислових задач.

Суть методу Гоморі (або методу відтинання) полягає в тому, що задачу лінійного цілочислового програмування розв’язують спочатку без умови цілочисельності. Якщо одержаний оптимальний розв’язок цілочисловий, то він є оптимальним розв’язком задачі цілочислового лінійного програмування. У протилежному випадку до умови початкової задачі додають лінійне обмеження:

,

де символ {} позначає дробову частину числа.

Метод «віток і меж»

Найбільш вживаним та більш ефективним за метод Гоморі є метод «віток і меж».

Спочатку розв’язується задача без умови цілочисленості (послаблену задачу).

Якщо отримали розв’язок тільки з цілими числами, то це оптимальний план задачі.

Якщо розв’язок містить дробові значення, то формулюють два додаткових обмеження:

або ,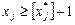

де —розв’язок послабленої задачі, який не задовольняє умову цілочисленості (у разі наявності декількох таких розв’язків вибирають той ціла частина якого більша), символ [ ] позначає цілу частину числа.

Потім незалежно одне від одного ці обмеження включають до вихідної системи обмежень. Тим самим отримують дві цілочислові задачі.

(6.5) за умов , , ; , — цілі,

за умов , , , , — цілі,

Розв’язуючи ці дві задачі отримують два умовно оптимальні плани. Якщо хоча б одна з задач дала цілочисловий розв’язок, то цей розв’язок приймають за оптимальний план задачі. Якщо знову не отримали цілочислового розв’язку, то далі аналогічним чином розгалужують ту задачу цільова функція якої набула більшого значення.

Розв’язати задачу цілочислового програмування.

,

Розв’язування.

Розв’язуємо задачу, нехтуючи умовою цілочисловості (таблиці 2.45-2.47).

Таблиця 2.45 – Перша симплекс-таблиця

Х баз	С баз	План		-1
х 1	х 2	х 3	х 4	х5	х 6
х 4				-1
х 5					-1				-
х 6					-1				-
		-1		-2

Таблиця 2.46 – Друга симплекс-таблиця

Х баз	С баз	План		-1
х 1	х 2	х 3	х 4	х5	х 6
х 3				-1
х 5
х 6
			-1

Таблиця 2.47 – Третя симплекс-таблиця

Х баз	С баз	План		-1
х 1	х 2	х 3	х 4	х5	х 6
х 3
х 2	-1
х 6
	3,5

У симплекс-таблиці 2.47 оцінковий рядок задовольняє теорему оптимальності, отже ми отримали оптимальний план задачі:

.

Значення другої та третьої змінної є дробовим числом, що не задовольняє початкову умову цілочисленості.

Застосуємо метод Гоморі

Побудуємо для другого рядка наведеної симплексної таблиці додаткове обмеження виду :

.

Додаткове обмеження набирає вигляду:

.

Зведемо його до канонічної форми та введемо штучну змінну:

.

Приєднаємо здобуте обмеження до останньої симплексної таблиці з умовно-оптимальним планом, дістанемо (таблиця 2.48):

Таблиця 2.48 –Симплекс-таблиця

Х баз	С баз	План		-1					– М
х 1	х 2	х 3	х 4	х5	х 6	х 7
х 3
х 2	-1
х 6
х 7	– М							-1
	3,5
						М

Розв’язуючи остаточно наведену задачу, знаходимо цілочисловий оптимальний план: , .

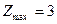Розв’яжемо задачу методом «віток і меж»

Розв’язуємо послаблену задачу, тобто нехтуючи умовою цілочисловості.

Отримаємо останню симплекс-таблицю (таблиця 2.49).

Таблиця 2.49 – Симплекс-таблиця

Х баз	С баз	План		-1
х 1	х 2	х 3	х 4	х5	х 6
х 3
х 2	-1
х 6
	3,5

Оскільки ми отримали декілька дробових розв’язків задачі, то виберемо з них той, що має більшу цілу частину (х ₃).

Запишемо дві умови:

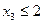та .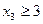

Розв’язуємо по черзі обидві утворені задачі, при цьому знову нехтуємо умовою цілочисловості.

, ,

, ,

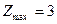
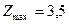
Цілочисловий план знайдено.

Зауваження. У випадку, якщо б жодна з двох задач не отримала б цілочислового розв’язку, то процес розв’язування необхідно продовжити, узявши для наступного розгалуження ту задачу, оптимальний план якої дає більше значення.

Завдання для індивідуальної та самостійної роботи студентів

Приклад. Розв’язати задачу цілочислового програмування.

Номер варіанта визначається за вказівкою викладача.

1.	16.
2.	17.
3.	18.
4.	19.
5.	20.
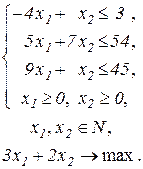
6.	21.
7.
8.	23.
9.	24.
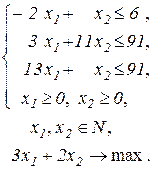
10.	25.
11.	26.
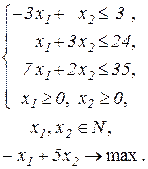
12.	27.
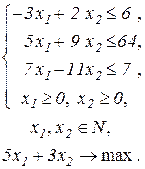
13.	28.
14.	29.
15.	30.

2.9 Транспортна задача (ТЗ)

Дата добавления: 2017-02-01