Метод потенціалів

Визначимо тип транспортної задачі (відкрита чи закрита). Якщо задана задача відкрита, то:

- у випадку перевищення загального попиту над за­­пасами 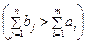на величину вводять фіктивного умовного постачальника ;

- у випадку перевищення запасів над попитом на величину вводять фіктивного умовного споживача .

При цьому вважають вартість перевезення одиниці продукції для фіктивного постачальника або фіктивного споживача рівною нулю.

Побудуємо початковий опорний план транспортної задачі. Після цього будемо послідовно його покращувати до отримання оптимального плану.

Для складання початкового опорного плану можна використати кілька методів: північно-західного кута; мінімальної вартості; подвійної переваги; апроксимації Фогеля.

Метод північно-західного кута.

Починають із заповнення лівої верхньої клітинки таблиці (х ₁₁), в яку записують менше з двох чисел а ₁ та b ₁. Далі переходять до наступної клітинки в рядку або у стовпчику і заповнюють її, і т. д. Закінчують заповнювати таблицю у правій нижній клітинці.

Метод мінімальної вартості

1. У клітинку з мінімальною вартістю записують найбільшу можливу кількість продукції.

2. Коректують залишок записів та попиту.

3. Вибирають наступну клітинку з найменшою вартістю, у яку поміщають найбільшу можливу кількість продукції (так продовжують доти поки запаси та попит дорівнюватимуть нулю).

Зауваження. Якщо найменше значення вартості відповідає більше ніж одній клітинці, то вибір здійснюється випадковим чином.

У опорному плані задачі повинно бути заповнено (m + n – 1) клітинок, де m — кількість постачальників; n — кількість споживачів у задачі, у тому числі фіктивних. Такий план називають невиродженим. Якщо заповнених клітинок у таблиці менш як (m + n – 1), то опорний план називають виродженим.

Приклад 1. Скласти початковий опорний план методом північно-західного кута.

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
Потреби

Розв’язання

Починаємо заповнення з верхньої лівої клітинки. Запишемо в неї .

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
Потреби

Переходимо по першому ряду до другої клітинки. У неї запишемо: .

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
Потреби

Переходимо до другої клітинки у другому стовпчику. У неї запишемо:

.

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
Потреби

Шляхом аналогічних міркувань заповнюємо повністю таблицю.

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
Потреби

Таким чином отримали такий опорний план задачі:

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
Потреби

Перевіримо задачу на невиродженість. Має бути (m + n – 1) клітинок, де m — кількість постачальників; n — кількість споживачів у задачі. У нашій задачі: . Тобто задачі невироджена (має розв’язок).

Приклад 2. Скласти початковий опорний план методом мінімальної вартості.

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
А4
Потреби

Розв’язання

Найменші вартості у розмірі 1 знаходяться у клітинках з індексами (1;2) та (2;3).

Запишемо у клітину з індексом (1;2) значення . Виключимо з розгляду другий стовпчик, оскільки всі потреби задоволені.

У клітину з індексом (2;3) занесемо значення . Третій стовпчик виключимо з розгляду.

Серед даних таблиці, що залишили, найменша вартість знаходиться у клітині (2;4). Заповнимо її: . Другий рядок виключимо з розгляду.

Серед даних, що залишились найменша вартість у клітині (1;4). Заповнимо її: . Перший рядок виключаємо з розгляду.

Серед даних, що залишились найменша вартість у клітині (3;4). Запишемо у неї: . Четвертий стовпчик виключимо з розгляду.

Серед даних, що залишились найменша вартість у клітині (3;1). Запишемо у неї: . Третій рядок виключимо з розгляду.

Залишила клітина (4;1). Запишемо у неї залишок по запасам та потребам: 180.

Пункт	Споживач	Запаси
В1	В2	В3	В4
А1
А2
А3
А4
Потреби

Перевіримо задачу на невиродженість. Має бути (m + n – 1) клітинок, де m — кількість постачальників; n — кількість споживачів у задачі. У нашій задачі: . Тобто задачі невироджена (має розв’язок).

Теорема (умова оптимальності опорного план транспортної задачі). Якщо для деякого опорного плану Х ^* = (x_ij ^*) існують числа u_i та v_j, для яких виконується умова

u_i + v_j = c_ij, при x_ij > 0,

u_i + v_j £ c_ij, при x_ij = 0

для всіх та , то він є оптимальним планом транспортної задачі.

Числа u_i та v_j ( та ) називають потенціалами відповідно запасів та споживачів.

Потенціали опорного плану визначаються із системи рівнянь
u_i + v_j = c_ij, які записують для всіх заповнених клітинок транспорт­ної таблиці.

За допомогою розрахованих потенціалів перевіряють умову оптимальності u_i + v_j £ c_ij для порожніх клітинок таблиці. Якщо хоча б для однієї клітинки ця умова не виконується, тобто u_i + v_j > c_ij, то поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.

Перехід від одного опорного плану до іншого виконують заповненням клітинки, для якої порушено умову оптимальності. Якщо таких клітинок кілька, то для заповнення вибирають таку, що має найбільше порушення, тобто . Для вибраної порожньої клітинки будують цикл перерахування та виконують перерозподіл продукції в межах цього циклу за такими правилами:

1) кожній вершині циклу приписують певний знак, причому вільній клітинці — знак «+», а всім іншим по черзі — знаки «–» та «+»;

2) у порожню клітинку переносять менше з чисел x_ij, що стоять у клітинках зі знаком «–». Одночасно це число додають до відповідних чисел, які розміщуються в клітинках зі знаком «+».

Отже, клітинка, що була вільною, стає заповненою, а відповід­на клітинка з мінімальним числом x_ij вважається порожньою. У результаті такого перерозподілу продукції дістанемо новий опор­ний план транспортної задачі.

Приклад, [2]

Компанія контролює три фабрики А ₁, А ₂, А ₃, здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір із чотирма замовниками В ₁, В ₂, В ₃, В ₄, яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовникам з кожної фабрики наведено в таблиці 2.51.

Таблиця 2.51 – Вихідні дані

Фабрика	Вартість виробництва і транспортування 1000 од. продукції за замовниками
В 1	В 2	В 3	В 4
А 1
А 2
А 3

Визначити для кожної фабрики оптимальний план перевезення продукції до замовників, що мінімізує загальну вартість виробництва і транспортних послуг.

Побудова математичної моделі. Нехай x_ij — кількість продукції, що перевозиться з і -ї фабрики до j -го замовника . Оскільки транспортна задача за умовою є збалансованою, закритою , то математична модель задачі матиме вигляд

Економічний зміст записаних обмежень полягає ось у чому: уся вироблена на фабриках продукція має вивозитися до замовників повністю.

Аналогічні обмеження можна записати відносно замовників: продукція, що надходить до споживача, має повністю задовольняти його попит. Математично це записується так:

Загальні витрати, пов’язані з виробництвом і транспортуванням продукції, складаються як добуток обсягу перевезеної продукції та питомої вартості перевезень за відповідним маршрутом і за умовою задачі мають бути мінімальними. Тому

Z = 4 × x ₁₁ + 4 × x ₁₂ + 2 × x ₁₃ + 5 × x ₁₄ + 5 × x ₂₁ + 3 × x ₂₂ + x ₂₃ +
+ 2 × x ₂₄ + 2 × x ₃₁ + x ₃₂ +4 × x ₃₃ +2 × x ₃₄ ® min.

У цілому математичну модель поставленої задачі можна записати так:

Z = 4 x ₁₁ + 4 x ₁₂ + 2 x ₁₃ + 5 x ₁₄ + 5 x ₂₁ + 3 x ₂₂ + x ₂₃ + 2 x ₂₄ +
+ 2 x ₃₁ + x ₃₂ +4 x ₃₃ +2 x ₃₄ ® min

Розв’язування. Розв’язування задачі подамо в таблицях, які назвемо транспортними. Перший опорний план задачі побудуємо методом мінімальної вартості (таблиця 2.52).

Таблиця 2.52 – Перша опорний план

Aj	Bj	ui
B 1= 110	B 2= 40	B 3= 60	B 4= 80
A 1= 150			2 +	40–	u 1= 5
A 2= 60			–60	0+	u 2= 2
A 3= 80					u 3= 2
vj	v 1= –1	v 2= –1	v 3= –1	v 4= 0

Тому Z = 4 × 110 + 5 × 40 + 1 × 60 + 1 × 40 + 2 × 40 = 820 ум. од.

Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п’яти, а (m + n – 1) = 3 + 4 – 1 = 6. Для подальшого розв’язування задачі необхідно в одну з порожніх клітинок записати «нульове перевезення» так, щоб не порушити опорності плану, тобто можна зай­няти будь-яку вільну клітинку, яка не утворює замкненого циклу. Наприклад, заповнимо клітинку А ₂ В ₄. Тепер перший план транспортної задачі є невиродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.

На основі першої умови оптимальності u_i + v_j = c_ij складемо систему рівнянь для визначення потенціалів плану:

Записана система рівнянь є невизначеною, і один з її розв’язків дістанемо, якщо, наприклад, v ₄ = 0. Тоді всі інші потенціали однозначно визначаються: u ₁ = 5, u ₂ = 2, u ₃ = 2, v ₁ = –1,
v ₂ = –1, v ₃ = –1.

Далі згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності u_i + v_j ≤ c_ij (для порожніх клітинок таблиці):

А ₁ B ₂: u ₁ + v ₂ = 5 + (–1) = 4 = 4;

А ₁ B ₃: u ₁ + v ₃ = 5 + (–1) = 4 > 2;

А ₂ B ₁: u ₂ + v ₁ = 2 + (–1) = 1 < 5;

А ₂ B ₂: u ₂ + v ₂ = 2 + (–1) = 1 < 3;

А ₃ B ₁: u ₃ + v ₁ = 2 + (–1) = 1 < 2;

А ₃ B ₃: u ₃ + v ₃ = 2 + (–1) = 1 < 4.

Умова оптимальності не виконується для клітинки А ₁ B ₃. Порушення D₁₃ = (u ₁ + v ₃) – c ₁₃ = 4 – 2 = 2 записуємо в лівому нижньому кутку відповідної клітинки.

Перший опорний план транспортної задачі є неоптимальним. Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці.

Потрібно заповнити клітинку А ₁ B ₃, в якій є єдине порушення умови оптимальності. Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки А ₁ B ₃, та позначаємо вершини циклу почергово знаками «–» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у вільну клітинку А ₁ B ₃ переносимо менше з чисел х_ij, які розміщуються в клітинках зі знаком «–». Одночасно це саме число х_ij додаємо до відповідних чисел, що розміщуються в клітинках зі знаком «+», та віднімаємо від чисел, що розміщуються в клітинках, позначених знаком «–».

У даному випадку , тобто . Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка А ₁ B ₃ — 40 од. продукції, А ₂ B ₃ – (60 – 40) = 20 од., А ₂ B ₄ – (0 + 40) = 40 од. Клітинка А ₁ B ₄, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (n + m – 1).

Отже, другий опорний план транспортної задачі матиме такий вигляд (таблиця 2.53):

Таблиця 2.53 – Другий опорний план

Aj	Bj	ui
B 1= 110	B 2= 40	B 3= 60	B 4= 80
A 1= 150	–110		40+		u 1= 0
A 2= 60			–20	40+	u 2= –1
A 3= 80	1 +			40–	u 3= –1
vj	v 1= 4	v 2= –2	v 3= 2	v 4= 3

Тому Z ₂ = 4 × 110 + 2 × 40 + 1 × 20 + 2 × 40 + 1 × 40 + 2 × 40 =
740 ум. од.

Новий план знову перевіряємо на оптимальність, тобто повторюємо описані раніше дії. Другий план транспортної задачі також неоптимальний (порушення для клітинки А ₃ B ₁). За допомогою побудованого циклу виконаємо перехід до третього опор­ного плану транспортної задачі і дістанемо таку таблицю 2.54:

Таблиця 2.54 – Третій опорний план

Aj	Bj	ui
B 1= 110	B 2= 40	B 3= 60	B 4= 80
A 1= 150					u 1= 2
A 2= 60					u 2= 0
A 3= 80					u 3= 0
vj	v 1= 2	v 2= 1	v 3= 0	v 4= 2

Тому Z ₃ = 4 × 90 + 2 × 60 + 2 × 60 + 2 × 20 + 1 × 40 + 2 × 20 =
720 ум. од.

Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний. Тому

;

За оптимальним планом перевезень перший замовник отримує 90 тис. од. продукції з першої фабрики та 20 тис. од. — з третьої. Другий споживач задовольняє свій попит за рахунок виробництва та перевезення 40 тис. од. продукції з третьої фабрики і т. д. При цьому загальна вартість виробництва та перевезення всієї продукції є найменшою і становить 720 ум. од.

Завдання для індивідуальної та самостійної роботи студентів

Приклад. Однорідний вантаж, зосереджений у m постачальників в обсягах a_i () необхідно поставити n споживачам в обсягах b_j (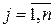). Відомі с_ij (; 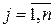) – вартості перевезення одиниці вантажу від кожного i -го постачальника до кожного j -го споживача. Необхідно скласти такий план перевезень, при якому запаси усіх постачальників вивозяться повністю й сумарні витрати на перевезення усього вантажу мінімальні. Запаси постачальників , потреби споживачів 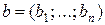та матриця вартостей задані нижче.

Номер варіанта визначається за вказівкою викладача.

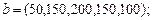
1.	16.
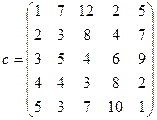
2.	17.
3.	18.
4.	19.
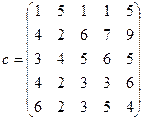
5.	20.
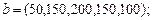
6.	21.
7.	22.
8.	23.
9.	24.
10.	25.
11.	26.
12.	27.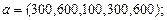
13.	28.
14.	29.
15.	30.

Дата добавления: 2017-02-01