Метод равномерного поиска

Методы оптимизации функций одной переменной

Алгоритм нахождения максимума функции

Простейшая задача нахождения максимума функции решается по следующему алгоритму:

1. Задаются границы a и b, в пределах которых имеется максимум функции.

2. Интервал [a,b] разбивается на определенное количество шагов.

3. Функция табулируется в пределах заданного интервала, и каждое вычисленное значение функции сравнивается с максимальным (заданным до начала табулирования).

4. Находится максимальное значение функции на заданном интервале с определенным шагом и выводится на печать.

БЛОК-СХЕМА АЛГОРИТМА ИМЕЕТ ВИД:

Рис. 4. Блок – схема алгоритма нахождения максимума функции

Естественно, что с уменьшением шага изменения аргумента точность вычисления максимума увеличивается.

Можно воспользоваться и следующим алгоритмом:

1. Найти значение максимума по алгоритму, представленному выше.

2. Для дальнейшего рассмотрения выбрать отрезок [xmax-dx, xmax+dx] и выполнить вычисление максимума с шагом, например, dx/10.

3. Сравнить два найденных значения.

max1 – значение максимума с шагом dx и max2 – значение максимума с шагом dx/10. Если |max2-max1| <=E (где Е – заданная степень точности вычисления), то закончить решение задачи и max2 вывести на печать, если нет, то вычисление продолжить дальше, повторяя п.2.

Такую задачу удобнее решать, используя процедуру нахождения максимального значения функции.

Блок – схема решения задачи имеет вид:

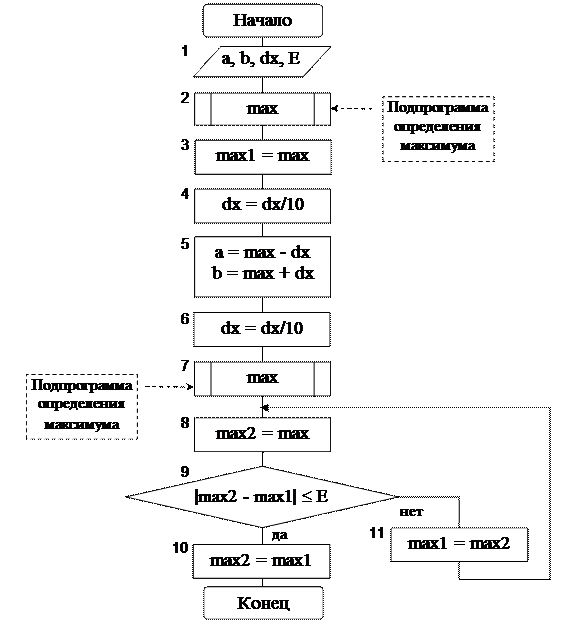
Рис. 5. Блок – схема алгоритма нахождения максимума функции

Этот метод основан на том, что переменной x присваиваются значения x+∆x с шагом ∆x = const и вычисляются значения F(x). Если F(x _n+1)>F(x_n), переменной x даётся новое приращение. Как только F(x_n+1)станет меньше F(x) поиск останавливается. При малой заданной погрешности этот метод неэкономичен по затратам машинного времени.

Дата добавления: 2017-02-01