
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная работа № 9
|
|
|
|
Примеры
- Найти общее решение дифференциального уравнения
 .
.
Это уравнение с разделяющимися переменными 1.1.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
Решение  .
.
- Найти общее решение дифференциального уравнения
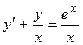 .
.
Это линейное уравнение I порядка 1.2. Замена 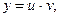
 ,
,  ,
,  ,
,  . Решаем
. Решаем  ,
,  ,
, 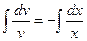 ,
,  ,
, 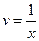 . Подставляем
. Подставляем  , т.е.
, т.е.  ,
,  ;
;  ,
, 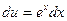
 ,
,  , тогда решение
, тогда решение 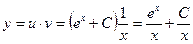 .
.
- Найти частное решение дифференциального уравнения
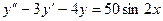 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 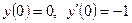 . Решаем по 2.1).
. Решаем по 2.1).
Решение. а) Однородное уравнение  (2.1.1). Характеристическое уравнение
(2.1.1). Характеристическое уравнение  .
.
б) Частное решение неоднородного уравнения (2.1.2) 
 ;
;  ;
;  .
.
Ищем 
 ;
;  . Подставим в неоднородное уравнение:
. Подставим в неоднородное уравнение: 

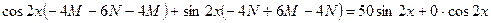 .Приравниваем коэффициенты при
.Приравниваем коэффициенты при 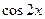 и
и  в левой и правой части тождества
в левой и правой части тождества
 . Итак,
. Итак,  .
.
в) Общее решение:  .
.
г) Найдём частное решение при начальных условиях (по 2.1.3):
 . Подставим начальные условия:
. Подставим начальные условия: 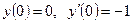
 . Частное решение: при
. Частное решение: при 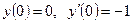 ;
; 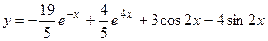 .
.
Варианты контрольной работы
Контрольная работа содержит 2 задания:
1) Найти общее решение дифференциального уравнения I порядка.
2) Найти частное решение дифференциального уравнения II порядка 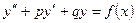 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 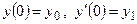 .
.
| . № вар-та | Задания |
1) 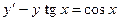 ; 2) ; 2) 
| |
1) 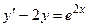 ; 2) ; 2) 
| |
1)  ; 2) ; 2) 
| |
1)  ; 2) ; 2) 
| |
1)  ; 2) ; 2) 
| |
1) 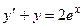 ; 2) ; 2) 
| |
1)  ; 2) ; 2) 
| |
1)  ; 2) ; 2) 
| |
1) 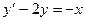 ; 2) ; 2) 
| |
1)  ; 2) ; 2) 
|
Тема: «Ряды»
Краткая теория.
1. Числовые ряды
1.0) 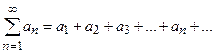 , Число
, Число 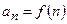 – общий или n -ый член ряда.
– общий или n -ый член ряда.
1.1) Сумма ряда. Пусть 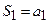 ,
,  .
.  называется n -ой частной суммой. Если существует
называется n -ой частной суммой. Если существует  , то ряд называется сходящимся, а число S – суммой ряда. Иначе ряд – расходящийся.
, то ряд называется сходящимся, а число S – суммой ряда. Иначе ряд – расходящийся.
1.2)  ;
; 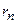 – остаток ряда. Если
– остаток ряда. Если  , то
, то  .
.
1.3) Необходимый признак сходимости ряда. Если ряд 1.0) сходится, то  . Применяется для доказательства расходимости ряда, таким образом:
. Применяется для доказательства расходимости ряда, таким образом:
1.3.1) Если  , то ряд
, то ряд  расходится.
расходится.
1.4) Знакоположительные ряды:  ,
,  . Достаточные признаки сходимости.
. Достаточные признаки сходимости.
1.4.1) Признаки сравнения.
Даны ряды (1)  и (2)
и (2)  .
.
1.4.1.2 – 1.4.1.3) Пусть  , начиная с
, начиная с  , где N = любое натуральное число.
, где N = любое натуральное число.
Если ряд  сходится, то ряд
сходится, то ряд  сходится.
сходится.
Если ряд  расходится, то ряд
расходится, то ряд  расходится.
расходится.
1.4.1.4.) Если 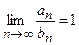 , то ряды
, то ряды  и
и  сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
1.4.2) Интегральный признак Коши.
Дан ряд  ,
, 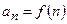 . Пусть
. Пусть  – монотонно убывающая функция, т.е.
– монотонно убывающая функция, т.е.  , тогда если: а)
, тогда если: а)  сходится, то
сходится, то  сходится; б)
сходится; б)  расходится, то
расходится, то  расходится.
расходится.
1.4.3) Признак Даламбера.
Дан ряд  . Пусть
. Пусть 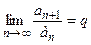 .
.
При  .
.
1.4.4) Радикальный признак Коши.
Дан ряд  . Пусть
. Пусть  . При
. При  .
.
1.5) Знакочередующиеся ряды.
1.5.0) Ряд 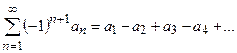 , где
, где 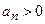 .
.
1.5.1) Признак Лейбница.
Пусть а)  , (
, ( – монотонно убывают); б)
– монотонно убывают); б)  , тогда ряд
, тогда ряд  сходится и его сумма
сходится и его сумма 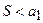 .
.
1.5.2) Следствие: Остаток ряда  . Если ряд
. Если ряд  сходится, то
сходится, то  . Остаток ряда по абсолютной величине меньше первого члена остатка.
. Остаток ряда по абсолютной величине меньше первого члена остатка.
1.6) Знакопеременный ряд.  , где
, где  имеют разные знаки.
имеют разные знаки.
1.7) Если ряд из абсолютных величин членов ряда  сходится, то ряд
сходится, то ряд  сходится абсолютно.
сходится абсолютно.
1.8) Если ряд  расходится, а ряд
расходится, а ряд  сходится, то говорят, что ряд
сходится, то говорят, что ряд  сходится условно.
сходится условно.
1.9) Знакочередующиеся ряды являются частным случаем знакопеременных рядов, поэтому, если для знакочередующегося ряда ряд из абсолютных величин  расходится, то надо применить признак Лейбница, чтобы проверить, сходится ли исходный ряд условно.
расходится, то надо применить признак Лейбница, чтобы проверить, сходится ли исходный ряд условно.
2. Степенные ряды
2.1)  ; Числа
; Числа  – коэффициенты ряда. При
– коэффициенты ряда. При  ряд
ряд  сходится,
сходится, 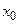 называется центром сходимости.
называется центром сходимости.
2.1.1) При  имеем ряд по степеням х:
имеем ряд по степеням х:  .
.
Заменой 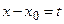 ряд 2.1) приводится к виду 2.1.1)
ряд 2.1) приводится к виду 2.1.1) 
2.2) Радиусом сходимости степенного ряда называется такое число R, что при всех х, таких, что  степенной ряд абсолютно сходится, а для всех х, таких, что
степенной ряд абсолютно сходится, а для всех х, таких, что  степенной ряд расходится. Интервал
степенной ряд расходится. Интервал  называется интервалом сходимости. При
называется интервалом сходимости. При  и
и  ряд может сходиться или расходиться. Это необходимо исследовать по признакам 1.3.1), 1.4.1), 1.4.2). Для рядов, расходящихся при всех х, кроме
ряд может сходиться или расходиться. Это необходимо исследовать по признакам 1.3.1), 1.4.1), 1.4.2). Для рядов, расходящихся при всех х, кроме  , радиус сходимости
, радиус сходимости  , а для рядов, сходящихся при всех х радиус сходимости
, а для рядов, сходящихся при всех х радиус сходимости  .
.
2.3) План нахождения интервала сходимости и радиуса сходимости  .
.
2.3.0) Дан ряд 
2.3.1) Составим ряд из абсолютных величин членов ряда 
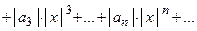 Интервалы сходимости рядов 2.3.0) и 2.3.1) одинаковы.
Интервалы сходимости рядов 2.3.0) и 2.3.1) одинаковы.
2.3.2) К ряду 2.3.1), все члены которого положительны, можно применить признак Даламбера или радикальный признак Коши.
Применение признака Даламбера:  . В точках х, в которых этот предел меньше 1, ряд сходится, а в которых он больше 1, ряд расходится, значение
. В точках х, в которых этот предел меньше 1, ряд сходится, а в которых он больше 1, ряд расходится, значение 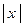 , при котором это предел равен 1, является значением радиуса сходимости
, при котором это предел равен 1, является значением радиуса сходимости  . Вид предела для определения интервала сходимости при применении радикального признака Коши
. Вид предела для определения интервала сходимости при применении радикального признака Коши  .
.
2.3.3) Исследуем сходимость числовых рядов на границах интервала сходимости по признакам 1.3.1), 1.4.1) или 1.4.2).
3. Разложение функции в степенные ряды.
3.1) Ряд Тейлора в окрестности 

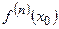 – значение n -ой производной функции
– значение n -ой производной функции  в точке
в точке  . Если
. Если  , то разложение по степеням х называется рядом Маклорена.
, то разложение по степеням х называется рядом Маклорена.
Таблица рядов Маклорена  в окрестности
в окрестности 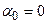 ,
,  – функция от х,
– функция от х, 
| № | Ряд | Интервал сходимости |
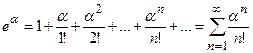
| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |
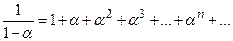
| 
| |

| 
| |

| 
| |

| 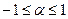
|
4. Применение рядов Тейлора
4.1) Вычисление определённых интегралов с помощью разложения функции в степенной ряд и затем интегрирования его почленно.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 62; Нарушение авторских прав?; Мы поможем в написании вашей работы!