
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения контрольных заданий
|
|
|
|
Задание 1. В урне находится 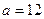 белых и
белых и  черных шаров. Из урны последовательно вынимают 2 шара. Найти вероятность, что оба разных цветов. Рассмотреть 2 ситуации:
черных шаров. Из урны последовательно вынимают 2 шара. Найти вероятность, что оба разных цветов. Рассмотреть 2 ситуации:
а) первый шар возвращают в урну
б) первый шар не возвращают в урну.
Решение: Событие А – два шара разных цветов.  Оно является суммой двух событий
Оно является суммой двух событий  . Событие
. Событие  есть произведение двух событий
есть произведение двух событий  ,
,  – вынут первый шар – белый;
– вынут первый шар – белый;  – второй шар – черный. Событие
– второй шар – черный. Событие  есть произведение двух событий
есть произведение двух событий  ,
, 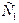 – вынут первый шар – черный;
– вынут первый шар – черный;  – второй шар – белый.
– второй шар – белый.
а) Первый вынутый шар возвращают в урну. При этом события  и
и  , а аналогично
, а аналогично 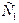 и
и  являются независимыми (по 1.4).
являются независимыми (по 1.4).  ;
; 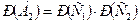 .
.
Найдем вероятность события  . Для него опыт – извлечение одного шара из урны. Общее число исходов опыта равно общему числу шаров
. Для него опыт – извлечение одного шара из урны. Общее число исходов опыта равно общему числу шаров 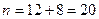 . Число исходов опыта, благоприятных для события
. Число исходов опыта, благоприятных для события  равно числу белых шаров
равно числу белых шаров  .
.  (по 1.2). Так как вынутый шар возвращают в урну, то рассуждая аналогично, получим
(по 1.2). Так как вынутый шар возвращают в урну, то рассуждая аналогично, получим  ;
;  ;
; 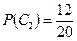 . По формуле (1.10)
. По формуле (1.10) 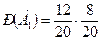 ;
;  . События
. События  и
и  , очевидно, несовместные (см. 1.3). По формуле (1.9)
, очевидно, несовместные (см. 1.3). По формуле (1.9)  ;
;  .
.
б) Первый шар после извлечения не возвращают в урну. При этом события  и
и  , а также
, а также 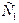 и
и  являются зависимыми (см. 1.4). По (1.12)
являются зависимыми (см. 1.4). По (1.12)  ;
;  . Вычислим условную вероятность
. Вычислим условную вероятность  события
события  при условии, что произошло событие
при условии, что произошло событие  и шар не вернули в урну. Осталось в урне
и шар не вернули в урну. Осталось в урне 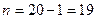 шаров, в том числе
шаров, в том числе 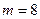 черных.
черных.  . Аналогично рассуждая, получим
. Аналогично рассуждая, получим  .
. 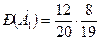 ;
;  (по 1.12). События
(по 1.12). События  и
и  – несовместные
– несовместные  .
.
Задание 2. В двух ящиках находятся детали. В первом ящике 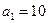 стандартных и
стандартных и  нестандартных деталей. Во втором ящике
нестандартных деталей. Во втором ящике  стандартных и
стандартных и  нестандартных деталей. Из первого ящика случайно вынули деталь и перенесли во второй ящик. После этого для контроля из второго ящика вынули деталь. Найти вероятность, что эта деталь – стандартная.
нестандартных деталей. Из первого ящика случайно вынули деталь и перенесли во второй ящик. После этого для контроля из второго ящика вынули деталь. Найти вероятность, что эта деталь – стандартная.
Решение: Надо найти вероятность события А – взятая из второго ящика деталь – стандартная. Опыт здесь производится при условии двух гипотез:
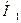 – из первого ящика сначала взяли и перенесли во второй стандартную деталь.
– из первого ящика сначала взяли и перенесли во второй стандартную деталь.
 – из первого ящика взяли и перенесли во второй нестандартную деталь.
– из первого ящика взяли и перенесли во второй нестандартную деталь.
Будем пользоваться формулой полной вероятности 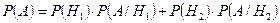 . Найдем вероятности
. Найдем вероятности 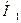 и
и  . Общее количество элементарных исходов опыта для
. Общее количество элементарных исходов опыта для 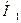 (а также для
(а также для  )
) 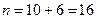 . Количество исходов опыта, благоприятных для
. Количество исходов опыта, благоприятных для 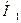 равно числу стандартных деталей
равно числу стандартных деталей  , а для
, а для  равно числу нестандартных деталей
равно числу нестандартных деталей  .
.  ;
;  ;
;  . При выполнении гипотезы
. При выполнении гипотезы 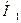 , во втором ящике станет
, во втором ящике станет  деталей, из них
деталей, из них  стандартных.
стандартных.  . При выполнении гипотезы
. При выполнении гипотезы  во втором ящике станет
во втором ящике станет 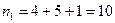 деталей, в том числе
деталей, в том числе  стандартных.
стандартных.  . По (1.13)
. По (1.13)  .
.
Задание 3. Дискретная случайная величина Х задана рядом распределения.
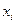
| -2 | -1 | ||

| 0,15 | 0,2 | 0,4 | 0,25 |
Найти функцию распределения  , построить её график. Вычислить
, построить её график. Вычислить  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию 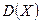 , средне квадратическое отклонение
, средне квадратическое отклонение 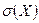 .
.
 Решение: Найдём функцию распределения
Решение: Найдём функцию распределения  .
. 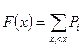 (по 2.3.2). Рассмотрим
(по 2.3.2). Рассмотрим  в интервалах между значениями
в интервалах между значениями  .
. 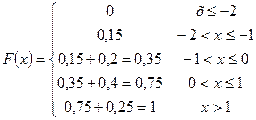
по (2.2.1)  =
=  .
.

 Математическое ожидание по (3.1).
Математическое ожидание по (3.1).








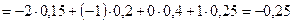 ;
;  .
.
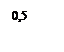 Дисперсия по (3.2)
Дисперсия по (3.2)









 .
.


 Среднее квадратическое отклонение (по 3.3)
Среднее квадратическое отклонение (по 3.3)
 .
.
Задание 4. Непрерывная случайная величина Х задана функцией плотности вероятностей.  . Найти число k, функцию распределения
. Найти число k, функцию распределения  случайной величины Х. Построить график
случайной величины Х. Построить график  и
и  . Вычислить математическое ожидание
. Вычислить математическое ожидание  и дисперсию
и дисперсию 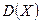 .
.
Решение: Найдем число  по (2.4.3)
по (2.4.3)  ;
; 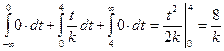 ;
;  . Найдем
. Найдем  по (2.4.2)
по (2.4.2)  . Рассмотрим
. Рассмотрим  при значениях х на данных интервалах
при значениях х на данных интервалах

 .
.

 .
.

 .
.

 Графики
Графики


















Математическое ожидание по (3.1)
 .
.  .
.
Дисперсия по (3.2)  .
.
Задание 5. Дана нормальная случайная величина  . Найти вероятность попадания этой случайной величины в заданный интервал
. Найти вероятность попадания этой случайной величины в заданный интервал  . Построить схематический график плотности вероятности
. Построить схематический график плотности вероятности  .
.
Решение: Вероятность попадания случайной величины  (см. 4.5)
(см. 4.5)  . Значение
. Значение  и
и  находится по таблице функции Лапласа из приложения I. Схематический график
находится по таблице функции Лапласа из приложения I. Схематический график  – колоколообразная кривая (см. 4.1)
– колоколообразная кривая (см. 4.1)  .
.  . Точка перегиба
. Точка перегиба 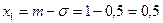 ;
;  .
.  .
.  .
.
 f(x)
f(x)











Варианты контрольной работы № 10
Контрольная № 10 содержит 5 заданий.
Задание 1. В урне находится а белых и b черных шаров. Из урны последовательно вынимают 2 шара. Найти вероятность, что оба разных цветов. Рассмотреть 2 ситуации:
а) первый шар возвращают в урну
б) первый шар не возвращают в урну.
Задание 2. В двух ящиках находятся детали. В первом ящике  стандартных и
стандартных и  нестандартных деталей. Во втором ящике
нестандартных деталей. Во втором ящике  стандартных и
стандартных и  нестандартных деталей. Из первого ящика случайно вынули деталь и перенесли во второй ящик. После этого для контроля из второго ящика вынули деталь. Найти вероятность, что эта деталь – стандартная.
нестандартных деталей. Из первого ящика случайно вынули деталь и перенесли во второй ящик. После этого для контроля из второго ящика вынули деталь. Найти вероятность, что эта деталь – стандартная.
Задание 3. Дискретная случайная величина Х задана рядом распределения
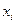
| -1 | |||

| 
| 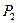
| 
| 
|
Найти функцию распределения  , построить её график. Вычислить
, построить её график. Вычислить  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию 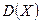 , средне квадратическое отклонение
, средне квадратическое отклонение 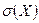 .
.
Задание 4. Непрерывная случайная величина Х задана функцией плотности вероятностей  . Найти число k, функцию распределения
. Найти число k, функцию распределения  случайной величины Х. Построить график
случайной величины Х. Построить график  и
и  . Вычислить математическое ожидание
. Вычислить математическое ожидание  и дисперсию
и дисперсию 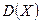 .
.
Задание 5. Дана нормальная случайная величина  . Найти вероятность попадания этой случайной величины в заданный интервал
. Найти вероятность попадания этой случайной величины в заданный интервал  . Построить схематический график плотности вероятности
. Построить схематический график плотности вероятности  .
.
Варианты значений параметров контрольных заданий
| № вар. Значение | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

| ||||||||||
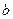
| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| 0,2 | 0,15 | 0,1 | 0,2 | 0,3 | 0,1 | 0,2 | 0,1 | 0,2 | 0,1 |

| 0,3 | 0,25 | 0,4 | 0,4 | 0,4 | 0,3 | 0,3 | 0,25 | 0,3 | 0,5 |

| 0,3 | 0,3 | 0,3 | 0,15 | 0,1 | 0,4 | 0,4 | 0,3 | 0,4 | 0,3 |
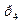
| 0,2 | 0,3 | 0,2 | 0,25 | 0,2 | 0,2 | 0,1 | 0,35 | 0,1 | 0,1 |

| -0,5 | -0,2 | -0,8 | -0,3 | -0,4 | 0,2 | 0,1 | -0,1 | 0,2 | -0,1 |
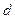
| 0,4 | 1,2 | 1,8 | 0,7 | 1,2 | 1,2 | 1,5 | 0,5 | 1,3 | 1,1 |

| 1/2 | 1/4 | 1/3 | 1/5 | 2/5 | 3/4 | 2/3 | |||
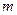
| ||||||||||

| ||||||||||

| ||||||||||

|
Литература
- Щипачев В.П. Высшая математика. М. Высшая школа. 1982-2003 гг.
- Кудрявцев В.А., Демидович Б.П. Курс высшей математики. М. Наука. 1975-1992 гг.
- Письменный Д. Конспект лекций по высшей математике. I часть. Айрис Пресс Рольф. М. 2000 г.
- Данко П.Е. и др. Высшая математика в упражнениях и задачах. М. Высшая школа. 1980-2006 гг.
- Запорожец Г.И. Руководство к решению задач по математическому анализу. М. Высшая математика. 1964 г.
- Пискунов Н.С. Дифференциальное и интегральное исчисление. М. Наука. 1970-2000 гг.
- Гмурман В.Е. Теория вероятностей и математическая статистика. М. 1977-2006 гг.
- Методические указания к контрольным работам кафедры ВМ и ММ РГГРУ.
Номер варианта каждой контрольной работы совпадает с последней цифрой учебного номера студента (номера зачетной книжки).
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 80; Нарушение авторских прав?; Мы поможем в написании вашей работы!