Адиабатный процесс. Вывод закона Пуассона. Работа газа в адиабатном процессе.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы.

Вывод:Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что

(55.1), т. е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражения (52.1) и (53.4), для произвольной массы газа перепишем уравнение (55.1) в виде (55.2). Продифференцировав уравнение состояния для идеального газа получим (55.3). Исключим из (55.2) и (55.3) температуру Т.

Разделив переменные и учитывая, что Сp/СV=g (см. (53.8)), найдем

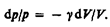Интегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, а затем потенцируя, придем к выражению

Так как состояния 1 и 2 выбраны произвольно, то можно записать (55.4). Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем урав­нение (55.1) в виде Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьша­ется от T1 до T2 и работа расширения идеального газа

(55.8)

Применяя те же приемы, что и при выводе формулы (55.5), выражение (55.8) для работы при адиабатическом расширении можно преобразовать к виду

где .

44. Циклические процессы. Цикл Карно. Что происходит с внутренней энергией и энтропией рабочего тела на различных участках цикла Карно, какая на них совершается работа? Выведите формулу для к.п.д. цикла Карно.

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. Работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой.

Цикл Карно: состоит из двух изотерм и двух адиабат.

Пусть в цилиндре под поршнем находится некоторое количество газа с параметрами р₁, V₁, Т₁. При взаимодействии с нагревателем рабочее тело изотермически расширяется с подводом теплоты Q₁ (процесс 1-2). Работа в процессе: .

В точке 2 цилиндр изолируется от нагревателя и газ продолжает расширяться адиабатно в процессе 2-3. В этом процессе в работу расширения превращается часть внутренней энергии газа и его температура понижается до Т₂, равной температуре холодильника. Работа процесса:

. Сжатие рабочего тела происходит за счет энергии, накопленной в маховике. Газ сжимается изотермически при взаимодействии с холодильником и передает ему количество теплоты Q₂. Работа в процессе 3-4: .

В точке 4 рабочее тело изолируется от холодильника и дальнейшее сжатие происходит адиабатно с повышением температуры газа до Т₁. Работа в процессе 4-1: . Работа цикла складывается из работ, совершенных в каждом процессе, причем, как видно из приведенных формул, работы в адиабатных процессах при суммировании взаимно уничтожаются:

.

Используя связь между параметрами в адиабатном процессе , можно показать, что

. Тогда с учетом выражение для термического КПД цикла будет иметь вид:

.

Для обратимого адиабатного процесса энтропия системы в процессе остается постоянной. Изотермический процесс .

45. Что понимается под термодинамической вероятностью состояния системы? Дайте статистическое и термодинамическое определения энтропии. Изменяется ли статистический вес состояния термодинамической системы при протекании обратимого адиабатического процесса?

Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние.

Термодинамическое определение энтропии: изменение энтропии термодинамической системы при обратимом процессе это отношение общего количества тепла ΔQ к величине абсолютной температуры T (то есть тепло, переданное системе, при постоянной температуре): 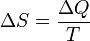.Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

, где dS — приращение (дифференциал) энтропии некоторой системы, а δQ — бесконечно малое количество теплоты, полученное этой системой.

Статистическое определение энтропии: Людвиг Больцман установил связь энтропии с вероятностью данного состояния. Позднее эту связь представил в виде формулы Макс Планк:

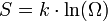, где константа k = 1,38×10⁻²³ Дж/К названа Планком постоянной Больцмана, а Ω — статистический вес состояния, является числом возможных микросостояний (способов) с помощью которых можно перейти в данное макроскопическое состояние.

Статистический вес (термодинам вероятность)-число способов, которыми может быть реализовано данное макроскопич.состояние системы. Термодинамически равновесное макроскопич. Состояние системы характеризуется определ.значениеми полной энергии,полного числа частиц и объема системы. Микроскопич.состояние системы соответствует заданному распределению её частиц по возможным классич.или квантовым состояниям.

Дата добавления: 2017-02-01