Выведите дифференциальное уравнение затухающих гармонических колебаний и запишите его решение. Дайте определение логарифмического декремента затухания.

Пусть в системе действует сила вязкого трения, т. е. сила направленная против скорости движения груза, модуль которой прямо пропорционален скорости (см. рис. 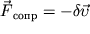1.2.1). (1.2.1.)

Запишем уравнение движения груза, составленное по 2-му закону Ньютона: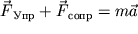

Подставим выражения для сил, тогда (6). Преобразуем выражение (6) к виду 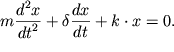Введем обозначения 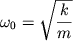(частота собственных незатухающих колебаний или собственная частота) и 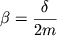(коэффициент затухания), окончательно получим 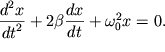(7). Выражение (7) - это дифференциальное уравнение свободных гармонических затухающих колебаний. Решение уравнения (7) будем искать в виде: 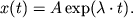(8). Подставим (8) в (7) получим 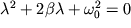. Из полученного выражения найдем значения : Если 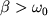(случай большого сопротивления), тогда имеем апериодическое решение в виде. Тогда решение будет в виде или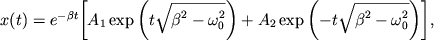
т.е. получаем затухающее движение. Если 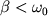, тогда 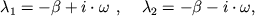(9), где 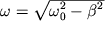- частота гармонических затухающих колебаний, т.е. получаем решение, соответствующее колебательному движению системы.

Логарифмический декремент затухания ϴ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. .

27. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Выведите формулу для расчета резонансной частоты.

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Линейное неоднородное дифференциальное уравнение: 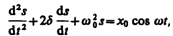(147.5) Применяем впоследствии его решение для вынужденных колебаний конкретной физической природы (x₀ в случае механических колебаний равно F₀/m, в случае электромагнитных — U_m/L).

Решение уравнения равно сумме общего решения (146.5) однородного урав­нения 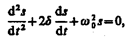и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме. Заменим правую часть уравнения (147.5) на комплексную величину х₀ :

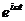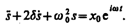(147.6). Частное решение этого уравнения будем искать в виде

Подставляя выражение для s и его производных в уравнение (147.6), получаем

(147.7). Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что h=w. Учитывая это, из уравнения (147.7) найдем величину s₀ и умножим ее числитель и знаменатель на

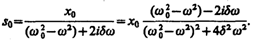. Это комплексное число удобно представить в экспоненциальной форм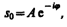е: , где (147.8); (147.9)

Следовательно, решение уравнения (147.6) в комплексной форме примет вид

Его вещественная часть, являющаяся решением уравнения (147.5), равна 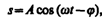(147.10)

где А и j задаются соответственно формулами (147.8) и (147.9).

Таким образом, частное решение неоднородного уравнения (147.5) имеет вид

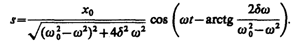(147.11). Решение уравнения (147.5) равно сумме общего решения однородного уравнения (147.12). (см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w.

РЕЗОНАНС - частотно-избирательный отклик колебат. системы на периодич. внеш. воздействие, при к-ром происходит резкое возрастание амплитуды стационарных колебаний. Наблюдается при приближении частоты внеш. воздействия к определённым, характерным для данной системы значениям. В линейных колебат. системах число таких резонансных частот соответствует числу степеней свободы и они совпадают с частотами собственных колебаний. В нелинейных колебат. системах, реактивные и диссипативные параметры к-рых зависят от величины стороннего воздействия, Р. может проявляться и как отклик на внеш. силовое воздействие, и как реакция на периодич. изменение параметров. В строгом значении термин "Р." относится лишь к случаю силового воздействия.

Из формулы 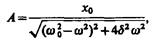следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту w_рез, — частоту, при которой амплитуда А сме­щения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкорен­ное выражение по w и приравняв его нулю, получим условие, определяющее w_рез: 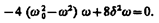Это равенство выполняется при w=0, ± , у которых только лишь положи­тельное значение имеет физический смысл. Следовательно, резонансная частота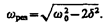

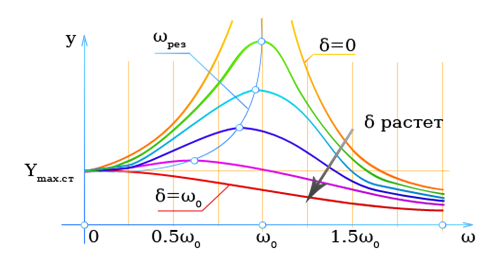
28. Какое явление называют резонансом? При каких колебаниях имеет место это явление? Получите формулу, связывающую резонансную частоту с собственной частотой и коэффициентом затухания колебательной системы. Начертите резонансные кривые для различных значений коэффициента затухания.

Определение и вывод в 27.

29. Что такое волна? Уравнение бегущей плоской гармонической волны.

Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры^[1]».

Уравнение колебаний частиц, лежащих в плоскости х, имеет вид (154.1)

откуда следует, что x(х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то

В общем случае уравнение плоской волны, распространяющейся вдоль положитель­ного направления оси х в среде, не поглощающей энергию, имеет вид 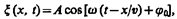(154.2)

где А = const — амплитуда волны, w — циклическая частота, j₀ — начальная фаза вол­ны, определяемая в общем случае выбором начал отсчета х и t, [w (t—x/v)+ j₀] — фаза плоской волны.

30. Что называют волной? Продольные и поперечные волны. Запишите волновое уравнение и уравнение плоской гармонической бегущей волны. Различаются ли уравнения для продольной и поперечной волн? Дайте определения длины волны и волнового числа.

Волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например, плотности вещества, напряжённости электрического поля, температуры. Более правильное определение: Волна — это явление распространения в пространстве с течением времени возмущения физической величины.

Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и попереч­ные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распростране­ния волны.

Волновое: Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных 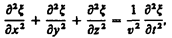или 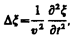(154.9), где v — фазовая скорость, — оператор Лапласа. Решением урав­нения (154.9) является уравнение любой волны.Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид

Уравнение плоской волны: В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

Длина волны: Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l (рис. 220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е. 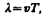или, учитывая, что T= 1/n, где n — частота колебаний…

Волновое число: величина, связанная с длиной волны λ соотношением: k = 2π/λ (число волн на длине 2π). В спектроскопии В. ч. часто называют величину, обратную длине волны (1/λ).Для характеристики волн используется волновое число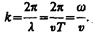

31. Уравнение плоской гармонической волны. Фазовая и групповая скорость волны. Получите выражение, связывающее фазовую и групповую скорости. Уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид ; 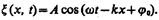(154.4)

Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера 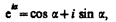(140.7), уравнение плоской волны можно записать в виде 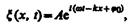Предположим, что при волновом процессе фаза постоянна, т. е. 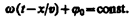(154.5). Продифференцировав выражение (154.5) и сократив на w, получим откуда (154.6). Следовательно, скорость v распространения волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.

Групповая скорость: За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии, что tdw —xdk = const, получим

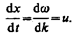(155.1). Эта скорость и есть групповая скорость.

Связь: Рассмотрим связь между групповой (см. (155.1)) и фазовой v=w /k (см. (154.8)) скоростями. Учитывая, что k=2p/l (см. (154.3)), получим

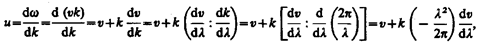или

Дата добавления: 2017-02-01