Пружинный маятник. Выведите дифференциальное уравнение его свободных незатухающих колебаний и запишите его решение.

Момент инерции материальной точки (тела) относительно оси. В чем заключается физический смысл момента инерции. Выведите формулу для момента инерции стержня относительно оси симметрии. Сформулируйте теорему Штейнера. Приведите пример ее применения.

Момент инерции тела относительно оси. Доказательство теоремы Штейнера. Моменты инерции однородных тел (стержня, цилиндра, шара) относительно осей симметрии.

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс л материальных точек системы на квадраты их расстояний до рассматриваемой оси:

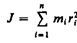
Для доказательства теоремы Штейнера рассмотрим тело произвольной формы.

Возьмем две параллельные оси ОО и О’О’, причем ось ОО проходит

через центр симметрии тела и совпадает с осью OZ, а ось О’О’ совпадает с

осью О’Z’. Выберем систему координат так, чтобы оси ОХ и О’Х’ проходим через

центр инерции тела и совпадали.

Тогда для произвольной точки тела с массой ∆m координаты будут

связаны так; а – расстояние между осями. Квадрат расстояния точки ∆mi от оси ОО

равен:. Квадрат же расстояния ∆mi до оси О’О’ равен:; С учетом

получим момент инерции тела относительно оси ОО:.

Момент инерции тела относительно оси О’О’ с учетом (3) равен:.

Возведя в квадрат выражение, стоящее в круглых скобках, и

сгруппировав слагаемые, получим:.

Первая сумма полученного равенства (6) тождественна с (4), т.е. дает момент инерции , вторая сумма дает , третья сумма равна 0, т.к. ось Z проходит через центр инерции тела, а это значит, что координата центра инерции равна нулю.

Вместе с тем по определению, откуда и следует, что

Таким образом выражение (6) примет вид:, что и требовалось доказать.

Момент инерции материальной точки относительно оси - произведение массы материальной точки на квадрат ее расстояния до оси.

Момент инерции — мера инертности тела при вращательном движении

Момент инерции стержня: Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна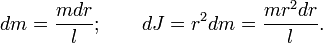

Интегрируя, получим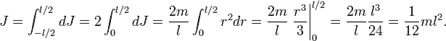

Теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_C относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

Пример: Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью C) равен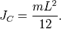

Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен где d — расстояние между искомой осью и осью C. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле d = L / 2:

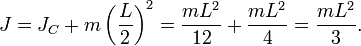
17. Что называют моментом импульса системы относительно данной точки? Выведите закон изменения момента импульса системы частиц. Сформулируйте закон сохранения момента импульса.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произ­ведением:

, где r — радиус-вектор, проведенный из точки О в точку A, p=mv — импульс мате­риальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Выведение: Модуль вектора момента импульса

где a — угол между векторами r и р, l — плечо вектора р относительно точки О.

Можно показать, что имеет место векторное равенство (19.3)

В замкнутой системе момент внешних сил откуда 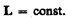(19.4)

Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы от­счета (относительно поворота замкнутой системы в пространстве на любой угол).

Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F=-kx, где k — жесткость пружины. Уравнение движения маятника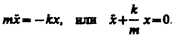

Выведение: Если можно пренебречь силами сопротивления движению и трением, то при выведении системы из положения равновесия на груз будет действовать только сила упругости пружины.

Запишем уравнение движения груза, составленное по 2-му закону Ньютона:

Спроектируем уравнение движения на ось X, при этом учтем, что сила упругости пропорциональна смещению из положения равновесия и направлена в сторону ему противоположную, а ускорение - это вторая производная координаты по времени. Тогда:

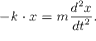(1). Преобразуем выражение (1) к виду

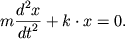Введем обозначение 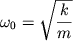(частота собственных незатухающих колебаний или собственная частота), окончательно получим (2). Выражение (2) - это дифференциальное уравнение свободных гармонических незатухающих колебаний.

Решение уравнения (2) будем искать в виде: 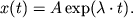(3). Подставим (3) в (2) получим

Из полученного выражения найдем значения : 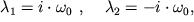(4) где Тогда .

Дата добавления: 2017-02-01