Как рассчитывается кинетическая энергия релятивистской частицы, полная энергия и энергия покоя. Взаимосвязь полной энергии и импульса.

Кинетическая энергия: приращение кинетической энергии материальной точки на элементарном переме­щении равно работе силы на этом перемещении: (40.1)

Учитывая, что dr = v d t, и подставив в (40.1) выражение (39.2), получаем

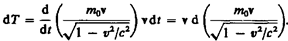Преобразовав данное выражение с учетом того, что vdv = v d v, и формулы (39.1), придем к выражению 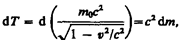(40.2) т. е. приращение кинетической энергии частицы пропорционально приращению ее массы. Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя m ₀, то, проинтегрировав (40.2), получим 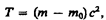(40.3) или кинетическая энергия релятивистской частицы имеет вид

(40.4). Выражение (40.4) при скоростях v«c переходит в классическое:

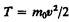
Полная энергия: А. Эйнштейн обобщил положение (40.2), предположив, что оно справедливо не только для кинетической энергии частицы, но и для полной энергии, а именно любое изменение массы D m сопровождается изменением полной энергии частицы, 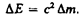(40.5). Отсюда А. Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой т:

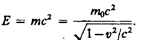(40.6). Закон (40.6) можно, учитывая выражение (40.3), записать в виде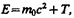

откуда следует, что покоящееся тело (T =0) также обладает энергией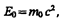

называемой энергией покоя. В классической механике энергия покоя Е ₀ не учитывается, считая, что при v =0 энергия покоящегося тела равна нулю.

Взаимосвязь энергии и импульса:

Из формул (40.6) и 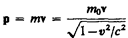найдем релятивистское соотношение между полной энергией и импульсом частицы: (40.7). Возвращаясь к уравнению (40.6), отметим еще раз, что оно имеет универсальный характер. Оно применимо ко воем формам энергии, т. е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса 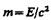(40.8) и, наоборот, со всякой массой связана энергия (40.6).

13. Уравнение движения тела в неинерциальных системах отсчета. Что такое силы инерции? Классифицируйте силы инерции по характеру движения неинерциальной системы отсчета и тела в ней.

Уравнение движения: Чтобы описать движение тел в неинерциальной системе отсчета, необходимо указать способ определения сил инерции. В инерциальной системе отсчета уравнение движения тела имеет вид 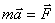. С учетом сил инерции в неинерциальной системе отсчета это уравнение примет вид 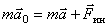. Отсюда 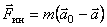. Разность ускорений 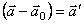равна ускорению, с которым неинерциальная система отсчета движется относительно инерциальной. Это ускорение иногда называют переносным. Таким образом, выражение для сил инерции в движущейся прямолинейно неинерциальной системе отсчета имеет вид 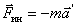, то есть сила инерции направлена противоположно переносному ускорению.

С и ла ин е рции это векторная величина, численно равная произведению массы т материальной точки на ее ускорение w и направленная противоположно ускорению.

Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными. Однако законы динамики можно применять и для них, если кроме сил, обусловленных воздействием тел друг на друга, ввести в рассмотрение силы особого рода — так называемые силы инерции.

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому в общем случае нужно учитывать следующие случаи проявления этих сил: 1) силы инерции при ускоренном поступательном движении системы отсчета(); 2) силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета (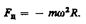); 3) силы инерции, действующие на тело, движущееся во вращающейся системе отсчета(F_к 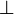v').

Дата добавления: 2017-02-01