Момент инерции. Вывести формулу для момента инерции сплошного диска относительно оси симметрии. Теорема Штейнера, ее вывод.

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс материальных точек системы на квадраты их расстояний до рассматриваемой оси: 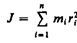. В случае непрерывного распределения масс эта сумма сводится к интегралу , где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.

Момент инерции диска: Поскольку диск однороден, плотность можно вынести из-под знака интеграла. Элемент объема диска dV = 2πr·b·dr, где b— толщина диска. Таким образом,

(1.96), где R — радиус диска. Введя массу диска, равную произведению плотности на объем диска π·R² b, получим: .

Теорема Штейнера: Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:

Момент инерции, по определению: . Радиус-вектор можно расписать как разность двух векторов: , где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

. Вынося за сумму , получим:

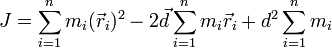. Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю: . Тогда:

Откуда и следует искомая формула: , где J_C — известный момент инерции относительно оси, проходящей через центр масс тела.

Дата добавления: 2017-02-01