Методы теоретического исследования тепловых полей при лазерной обработке

Наиболее просто параметры полей при лазерной обработке можно вычислять по известным аналитическим выражениям, которые представляют собой решения дифференциальных уравнений теплопроводности в линейной постановке при линейных граничных условиях. Это означает, что коэффициенты теплофизических свойств (теплопроводность l_ти объемная теплоемкость c g, коэффициент теплоотдачи a_ти т.д.) считают не зависящими от температуры.

В случаях лазерной обработки отдельным сфокусированным импульсом или непрерывным сфокусированным излучением в течение короткого промежутка времени можно использовать решения, полученные для мгновенных сосредоточенных источников.

Процесс распространения теплоты Q мгновенного сосредоточенного источника, выделившегося на поверхности полубесконечного тела в начальный момент времени t = 0 в точке О (рис. 3.5) (мгновенный точечный источник), выражается уравнением

, (3.8)

где – коэффициент температуропроводности; – квадрат расстояния от источника теплоты до точки тела А с координатами x, y, z; T ₀ – исходная температура материала детали.

Рис. 3.5. Схема действия неподвижного линейного источника в пластине

Теплоотдача с поверхности хОу не учитывается, так как ее влияние на тепловые процессы в полубесконечном теле несравненно меньше по сравнению с распространением теплоты в теле путем теплопроводности.

Из формулы (3.8) следует, что температура точек тела в любой момент времени t прямо пропорциональна количеству введенной теплоты (рис. 3.6, а).

Рис. 3.6. Распределение температур в полубесконечном теле при действии мгновенного точечного источника:

а – различное количество введенной теплоты Q; б – различное расстояние R до O;
в – различная теплоемкость материала с g

Характер изменения температуры в точках на различных расстояниях R от точки О одинаковый: повышение температуры на начальной стадии, достижение максимальных значений и последующее уменьшение (рис. 3.6, б). При этом в более удаленных точках максимальная температура имеет меньшее значение и достигается позднее.

В точке О, где приложен мгновенный источник теплоты, в начальный момент времени t = 0 расчетная температура стремится к бесконечности. Температуры всех точек полубесконечного тела с течением времени стремятся к нулю.

В материале, имеющем большее значение коэффициента теплопроводности l_т при постоянной теплоемкости с g, распределение теплоты происходит интенсивнее. При этом максимальные значения температур в различных точках остаются одинаковыми, но в материале с большей теплопроводностью максимальные температуры достигаются быстрее.

Изменение теплоемкости с gпри постоянной теплопроводности l_т неоднозначно влияет на процесс распространения теплоты. Температура в различных точках тела уменьшается при одновременном замедлении процесса распространения теплоты. Это наглядно видно из сопоставления изменения температуры во времени в одной той же точке тела при различных значениях теплоемкости с g (рис. 3.6, в).

Формулой (3.8) можно пользоваться для приближенного вычисления температур при кратковременном действии лазерного источника на поверхность массивного тела.

Процесс распространения теплоты Q мгновенного линейного источника, выделившегося в тонкой пластине толщиной δ с равномерным распределением по толщине в начальный момент времени t = 0 в точке О, выражается уравнением

, (3.9)

где – квадрат расстояния от источника теплоты до точки А с координатами x, y; – коэффициент температуроотдачи, учитывающий поверхностную теплоотдачу в окружающую среду за счет конвекции и излучения.

С помощью формулы (3.9) можно вычислить приближенные значения температур при кратковременном действии линейного лазерного источника нагрева, например при импульсном или кратковременном непрерывном излучении, используемом при сварке точечного соединения в пластинах.

При длительном действии точечного источника в течение произвольного времени t можно использовать принцип наложения температур, заключающийся в соответствующем интегрировании выражения (3.8) по времени t. Для этого представляют время t действия непрерывного источника в виде совокупности бесконечно малых элементов dt' (рис. 1.3). Тогда в точке О за элемент времени dt' через t' с после начала действия выделится элементарное количество теплоты

, (3.10)

где q (t')– функция изменения интенсивности источника времени (рис. 3.7).

Рис. 3.7. Разбивка времени действия непрерывного источника на элементы

Элементарное количество теплоты dQ (3.10), распространяясь в теле в течение времени t – t', приводит к повышению температуры к моменту времени t, вычисляемому в соответствии с формулой (3.11)

. (3.11)

Для определения температуры Т (R, t)в момент t при действии непрерывного точечного источника на поверхности тела необходимо проинтегрировать выражение (3.11) по времени t:

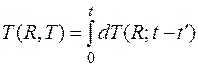. (3.12)

Подставим (3.10) и (3.11) в интеграл (3.12). Тогда

. (3.13)

Если на поверхности тела действует непрерывный точечный источник постоянной интенсивности q = const, то выражение (3.13) можно проинтегрировать в аналитическом виде:

, (3.14)

где Ф– функция интеграла вероятности, представленная в справочниках.

При достаточно длительном воздействии источника (t ®¥) температуры всех точек тела устремляются предельным значениям:

. (3.15)

Если точечный или линейный источники действуют какое-то произвольное время t,то можно использовать принцип наложения температур, заключающийся в соответствующем интегрировании выражений (3.8) или (3.9) по t.

Этот же принцип наложения используется для вывода уравнений процесса распространения теплоты при движущемся непрерывно действующем источнике. Соответствующие преобразования для произвольного времени действия подвижных источников сводятся к вычислению интеграла в числовом виде. Однако для установившегося (квазистационарного) состояния, которое наступает как предельное при длительном действии подвижного источника, можно получить аналитические выражения.

Уравнение квазистационарного состояния процесса распространения теплоты точечного источника постоянной тепловой мощности q, движущегося с постоянной скоростью v, по поверхности полубесконечного тела (рис. 3.8), имеет следующий вид

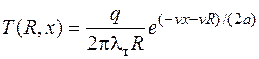, (3.16)

где R – постоянный радиус-вектор в подвижной системе координат, т.е. расстояние рассматриваемой точки А от начала 0 подвижной системы; х – абсцисса точки А в подвижной системе координат.

Оценка температурного поля, возникающего при термообработке или наплавке массивного тела сосредоточенным источником лазерного нагрева, может быть выполнена в первом приближении по формуле (3.16).

Рис. 3.8. Температурное поле предельного состояния при движении
точечного источника по поверхности полубесконечного тела:
q = 4000 Bт, v = 0,1 см/с, а = 0,1см²/с, l_т = 0,4 Дж/см·с·град:

а – изотермы и а поверхности хОу; б – изотермы в поперечной плоскости yOz, проходя щей через центр источника теплоты; в – распределение температуры по прямым, параллельным оси Ох и расположенным на поверхности массивного тела; г – распределение температуры
по прямым, параллельным оси Оу и лежащим в поперечной плоскости xOz;
д – схема расположения координатных осей

Уравнение квазистационарного состояния процесса распространения теплоты при нагреве пластины подвижным линейным источником постоянной мощности q, перемещающимся с постоянной скоростью v (рис. 3.9),следующее

, (3.17)

где r – плоский радиус-вектор в подвижной системе координат, связанной с источником теплоты; К ₀ – Бесселева функция от мнимого аргумента второго рода нулевого порядка, значение которой определяется по таблицам.

Рис. 3.9. Схема действия неподвижного линейного источника в пластине

Для приближенного описания температурного поля, возникающего при лазерной сварке встык пластин малой толщины или при лазерной резке пластин, можно использовать выражение (3.17).

В большинстве случаев технологические процессы лазерной обработки ведут с высокими скоростями, что дает основания некоторого упрощения формул за счет введения так называемых мощных быстродвижущихся источников.

Уравнение предельного состояния процесса распространения теплоты мощного быстродвижущегося источника в полубесконечном теле (рис. 3.10, 3.11) имеет вид

, (3.18)

где t – время, отсчитываемое от момента, когда источник пересекает плоскость у ₀ Оz ₀,проведенную перпендикулярно к оси движения источника через рассматриваемую точку А; у ₀, z ₀ – неподвижные координаты точки А, связанные с изделием, совпадающие с подвижными координатами у, z.

Рис. 3.10. Мощный быстродвижущийся точечный источник
на поверхности полубесконечного тела

Рис. 3.11. Распределение температуры при движении
мощного быстродвижущегося точечного источника теплоты
по поверхности массивного тела (q = 21 000 Вт, v = 1 см/с):
а – распределение температуры по линиям, параллельным оси Ох;
б – изотермы на поверхности тела

Предельное состояние процесса распространения теплоты при нагреве пластины мощным быстродвижущимся линейным источником (рис. 3.12) описывается следующим уравнением

. (3.19)

Рис. 3.12. Схема действия быстродвижущегося линейного источника в пластине

Представленные выше уравнения получены для сосредоточенных источников. Теория распространения теплоты сосредоточенных источников позволяет успешно определять температурные поля в зонах, удаленных от источника на расстояния, превышающие диаметр пятна лазерного излучения d _пв 3-5 раз. Процессы распространения теплоты в зонах, расположенных ближе к источнику, можно достоверно описать лишь с учетом характера распределения плотности мощности в пятне лазерного излучения.

Рассмотрим простой случай, когда энергия излучения распределена равномерно по лазерному пятну. При лазерной поверхностной обработке короткими импульсами длительностью (где r _п– радиус пятна нагрева лазерного излучения) задача теплопроводности может рассматриваться в одномерном приближении. При этом понимают, что основной поток теплоты в материале распространяется нормально к поверхности в глубину тела, т.е. по оси Оz.

Одномерное по оси Оz температурное поле, создаваемое в полубесконечном теле однородным излучением с равномерным распределением энергии излучения, описывается следующим уравнением (при t > τ_и)

. (3.20)

где z – расстояние, отсчитываемое по оси Оz (рис. 3.13); ierfc – функция интеграла вероятности.

Рис. 3.13. Схема воздействия лазерного излучения:

1 – фокусирующая линза; 2 – лазерное излучение; 3 – обрабатываемая деталь

При 0 < t < τ_иуравнение (3.20) приводится к упрощенному виду

. (3.21)

В формулах (3.20) и (3.21) плотность мощности теплового источника q _п вычисляется по следующей зависимости .

В случае импульсного воздействия плотность мощности , где – мощность импульса, W _и – энергия импульса, τ_и – время импульса).

Для определения температуры на поверхности тела следует в выражение (3.20) подставить z = 0

. (3.22)

Для 0 < t < τ_ивыражение (3.22) упрощается и для приближенного вычисления температур в точке z = 0 на поверхности тела приводится к следующему виду

. (3.23)

С целью последующего вычисления протяженности по глубине зоны нагрева до температуры T удобнее использовать выражение для расчета температур в неявном виде, полученное при допущении ,

. (3.24)

где z – глубина прогрева до температуры T (z, t).

Из выражения (3.24) можно получить простую формулу для приближенного определения протяженности по глубине зоны нагрева до заданной температуры под действием импульса излучения

. (3.25)

Дата добавления: 2017-02-01