Потенциал и разность потенциалов электрического поля

Потенциал и разность потенциалов электрического поля. Связь напряженности электрического поля с его потенциалом

Так как потенциальная энергия системы электрических зарядов пропорциональна величинам зарядов, то, помещая в одну и ту же точку поля различные по величине заряды, будет изменяться потенциальная энергия.

Однако отношение потенциальной энергии системы зарядов к величине помещаемого в данную точку поля электрического заряда остается постоянным, следовательно, оно может служить характеристикой электрического поля.

Потенциальную энергию положительного единичного заряда, помещенного в данную точку поля, называют потенциалом электрического поля j. Потенциал электрического поля

. (1.31)

Если поле создано положительным точечным зарядом q, то

, (1.32)

где q – величина заряда, создающего электрическое поле;

r – расстояние от центра заряда до рассматриваемой точки поля.

Потенциал электрического поля системы точечных зарядов равен алгебраической сумме потенциалов полей, создаваемых отдельно взятым зарядом системы:

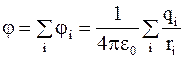, (1.33)

где q_i – величина i-го заряда;

r_i – расстояние от i-го заряда до рассматриваемой точки поля.

Из выражения (1.31)

W = qj. (1.34)

Так как работа сил электрического поля равна убыли потенциальной энергии, т.е.

A_1,2 = - DW = W₁ - W₂ = q(j₁ - j₂), (1.35)

то

. (1.36)

При q = q₊ = 1

. (1.37)

Таким образом, разность потенциалов между двумя точками поля, численно равна работе, которую совершают силы электрического поля по перемещению положительного единичного заряда из одной точки поля в другую.

При перемещении положительного единичного электрического заряда из данной точки поля в бесконечность

A_1,¥ = W₁ - W_¥ = qj_1,

а

. (1.38)

Если q = q₊ = 1, то

. (1.39)

Следовательно, потенциал электрического поля численно равен работе сил электрического поля по перемещению положительного единичного заряда из данной точки поля в бесконечность.

Потенциал и разность потенциалов электрического поля являются его энергетическими характеристиками. В системе СИ потенциал и разность потенциалов измеряются в вольтах.

Один вольт – это потенциал такой точки электрического поля, находясь в которой заряд в 1 Кл обладает потенциальной энергией, равной 1 Дж.

1.8.2. Связь напряженности электрического поля с его
потенциалом

Каждая точка электрического поля характеризуется напряженностью и потенциалом (силовой и энергетической характеристиками). Между ними должна существовать связь, которую можно установить исходя из следующих соображений.

Элементарная работа, совершаемая силами электрического поля по перемещению электрического заряда на расстояние dl,

dA = F∙dl∙cosa = F_l∙dl = qE_l∙dl.

Работа совершается за счет убыли (уменьшения) потенциальной энергии:

dA = - dW = - q×dj.

Следовательно, имеем

qE_l×dl = - q×dj.

Отсюда

, (1.40)

где характеризует быстроту изменения потенциала в данном направлении l и называется градиентом потенциала;

l – произвольно выбранное направление.

В векторной форме

E = - grad j. (1.41)

Знак "минус" означает, что вектор напряженности электрического поля направлен в сторону убывания потенциала.

Проинтегрировав формулу dj = - E_l×dl, получим

;

.

Откуда

, (1.42)

где d = l×cosa - расстояние между точками 1 и 2 поля.

В векторной форме выражение (1.41), можно представить так:

. (1.43)

Зная теорему Остроградского-Гаусса и связь между напряженностью и потенциалом электрического поля, можно по известной величине определить неизвестную.

Дата добавления: 2017-02-01