Электрическое поле, порождаемое бесконечно длинным, равномерно заряженным стержнем

Некоторые примеры электрических полей, порождаемых простейшими системами электрических зарядов

Формула Стокса

Уравнение Лапласа

Уравнение Пуассона

Дифференциальное уравнение потенциальности электростатического поля

Дифференциальная форма записи закона Кулона

Закон сохранения заряда в дифференциальной форме

Закон сохранения заряда в интегральной форме

Основные уравнения электростатики в вакууме

Уравнения электростатики устанавливают связь между основными характеристиками электростатического поля, характеризуют состояние такой системы, а следовательно, отображают законы электростатики. Основными законами и уравнениями электростатики являются:

, (1.46)

где r – объемная плотность заряда;

j – вектор плотности тока;

; (1.47)

; (1.48)

4) теорема Остроградского – Гаусса для непрерывного распределения зарядов

; (1.49)

rot E = 0; (1.50)

Dj = r/e₀, (1.51)

где - оператор Лапласа;

Dj = 0; (1.52)

. (1.53)

Характеристикой линейного распределения заряда является линейная плотность заряда. Физическая величина, численно равная заряду, находящемуся на единице длины, 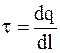. При равномерном распределении заряда .

Для определения напряженности электрического поля, порождаемого бесконечно длинным, равномерно заряженным стержнем, радиус которого R, воспользуемся теоремой Остроградского-Гаусса.

Для чего вокруг стержня проведем замкнутую (в рассматриваемом случае цилиндрическую) поверхность конечной длины, на боковой поверхности которой находится точка "А". Линии вектора E перпендикулярны оси стержня и боковой поверхности цилиндра (рис. 1.13).

Поток вектора напряженности электрического поля через построенную замкнутую цилиндрическую поверхность

, (1.54)

где Ф_o = 0, т.к. E_n = E×cosa = 0.

Следовательно

. (1.55)

На основании теоремы Остроградского-Гаусса

,

тогда

= ,

а

. (1.56)

Формула (1.56) справедлива не только для электрического поля заряженного стержня, но и для полей заряженных проводников, цилиндров, 2-х коаксиальных цилиндрических поверхностей, заряженных с одинаковой по величине линейной плотностью заряда t.

Для того чтобы определить разность потенциалов между двумя любыми точками такого поля, необходимо воспользоваться соотношением , откуда

.

Следовательно

,

а

, (1.57)

где r₁ и r₂ – соответственно расстояние от оси стержня (цилиндра) до рассматриваемых точек электрического поля.

Дата добавления: 2017-02-01