
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поток вектора напряженности электростатического поля
|
|
|
|
Число силовых линий вектора E на любом расстоянии от точечного заряда одно и то же.
 Пусть дан некоторый точечный заряд q. Проведем вокруг его некоторую замкнутую сферическую поверхность радиусом r (рис. 1.7). Полное число силовых линий N, пронизывающих поверхность S, равно произведению "густоты" силовых линий на величину поверхности. "Густота" силовых линий – это число силовых линий вектора E, приходящихся на единицу поверхности.
Пусть дан некоторый точечный заряд q. Проведем вокруг его некоторую замкнутую сферическую поверхность радиусом r (рис. 1.7). Полное число силовых линий N, пронизывающих поверхность S, равно произведению "густоты" силовых линий на величину поверхности. "Густота" силовых линий – это число силовых линий вектора E, приходящихся на единицу поверхности.
"Густота" силовых линий численно равна напряженности электрического поля в данном месте пространства. Численное значение вектора E на расстоянии, равном r от центра сферы (заряда q):
 . (1.13)
. (1.13)
Площадь сферической поверхности S = 4pr2, тогда число силовых линий, пронизывающих поверхность,
 . (1.14)
. (1.14)
Это свойство линий вектора E является общим для всех полей, создаваемых любой системой неподвижных электрических зарядов.
 Если в однородном электрическом поле с напряженностью E поместить некоторую площадку dS (рис. 1.8), ориентация которой в пространстве определяется с помощью положительной нормали n, то число силовых линий вектора E, пронизывающих данную площадку,
Если в однородном электрическом поле с напряженностью E поместить некоторую площадку dS (рис. 1.8), ориентация которой в пространстве определяется с помощью положительной нормали n, то число силовых линий вектора E, пронизывающих данную площадку,
dN = En×dS, (1.15)
где En = E× cosa - проекция вектора напряженности электрического поля на направление положительной нормали к поверхности dS;
a – угол между n и E.
Число силовых линий вектора E, пронизывающих произвольную поверхность S,
 . (1.16)
. (1.16)
Формула (1.16) определяет поток вектора E, пронизывающий поверхность S.
Таким образом, поток вектора напряженности электрического поля через поверхность S – это физическая величина, равная
 . (1.17)
. (1.17)
 В случае замкнутых поверхностей
В случае замкнутых поверхностей
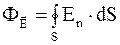 . (1.18)
. (1.18)
На рис. 1.9 представлен поток вектора напряженности электрического поля точечного заряда, который окружен сферической поверхностью с центром, совпадающим с центром точечного заряда, и поверхностью произвольной формы. Из рисунка видно, что число силовых линий вектора напряженности электрического поля E, выходящих из сферической поверхности, равно числу силовых линий вектора E, выходящих из произвольной поверхности. При этом принимается во внимание, что число дополнительных выходов силовых линий из произвольной поверхности полностью скомпенсировано числом дополнительных входов силовых линий в данную поверхность.
Принято считать поток вектора E, выходящий из области, охватываемой поверхностью, положительным, а входящий – отрицательным.
Поток вектора напряженности электрического поля точечного заряда через любую замкнутую поверхность
 . (1.19)
. (1.19)
1.5. Теорема Остроградского-Гаусса
для электрического поля в вакууме
Если внутри замкнутой поверхности находится система из n электрических зарядов, то поток вектора напряженности через данную поверхность (рис. 1.10)

 . (1.20)
. (1.20)
Таким образом, поток вектора напряженности электрического поля через произвольную замкнутую поверх-ность равен алгебраической сумме зарядов, находящихся внутри этой поверхности.
Данное утверждение носит название теоремы Остроградского-Гаусса.
При непрерывном распределении электрических зарядов с объёмной плотностью  внутри некоторой замкнутой поверхности, теорему Остроградского-Гаусса можно записать так:
внутри некоторой замкнутой поверхности, теорему Остроградского-Гаусса можно записать так:
 . (1.21)
. (1.21)
Теорема Остроградского-Гаусса позволяет определить величину заряда в любой области, в которой известна величина E, и упростить решение многих задач по определению напряженности электрических полей, созданных системами электрических зарядов.
1.6. Работа электрического поля по перемещению электрического заряда.
Циркуляция вектора напряженности электрического поля
 Если в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд qo (рис. 1.11), то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна
Если в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд qo (рис. 1.11), то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна
 (1.22)
(1.22)
где dr = dl×cosa.
Работа при перемещении заряда q из точки 1 в точку 2
 , (1.23)
, (1.23)
где k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ k = 1/4pe0;
q1 – заряд, создающий электрическое поле;
q2 – заряд, перемещаемый в электрическом поле;
r1, r2 – начальное и конечное расстояния между зарядами.
Из формулы (1.23) видно, что работа сил электрического поля по перемещению электрического заряда не зависит от траектории перемещения, а определяется только начальным и конечным положением зарядов. Следовательно, электростатическое поле электрических зарядов является потенциальным, а электростатические силы – консервативными силами.
Кроме того, из формулы (1.23) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
 . (1.24)
. (1.24)
Если в качестве заряда, переносимого в электростатическом поле, взять положительный единичный точечный заряд, то элементарная работа сил поля на пути d l равна dA = E ×d l = Eldl, где El = E×cosa - проекция вектора E на направление элементарного перемещения. Тогда формулу (1.24) можно записать в виде
 . (1.25)
. (1.25)
Интеграл
 (1.26)
(1.26)
называют циркуляцией вектора напряженности электростатического поля. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура (1.25) равна нулю. Равенство нулю циркуляции вектора напряженности электростатического поля еще раз подтверждает, что оно является потенциальным. Из потенциальности электростатического поля следует, что линии напряженности электростатического поля не могут быть замкнутыми – они начинаются и заканчиваются на зарядах или же уходят в бесконечность.
Надо отметить, что формула (1.25) справедлива лишь только для электростатического поля. Для электрических полей движущихся зарядов условие равенства нулю циркуляции вектора напряженности не выполняется. Для таких полей она отлична от нуля.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 49; Нарушение авторских прав?; Мы поможем в написании вашей работы!