
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Диполь в неоднородном внешнем электрическом поле
|
|
|
|
Если диполь помещен в неоднородное внешнее электрическое поле, то силы, действующие на заряды q+ и q-, не равны по величине и направлению, так как напряженность электрического поля в точках расположения зарядов не одинакова по величине, отличается на величину
 , (3.5)
, (3.5)
где a - угол между направлением вектора напряженности электрического поля E и направлением электрического дипольного момента p.
В этом случае на отрицательный заряд действует сила
 .
.
На положительный заряд действует сила
 .
.
Результирующая сила, действующая на диполь,
 (3.6)
(3.6)
 Под действием этой силы диполь будет либо втягиваться в область более сильного поля (
Под действием этой силы диполь будет либо втягиваться в область более сильного поля ( ), либо выталкиваться из него (
), либо выталкиваться из него (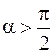 ) (рис. 3.4).
) (рис. 3.4).
Такое же действие оказывает электрическое поле на молекулы диэлектрика.
3.2. Свободные и связанные (поляризационные) заряды
в диэлектриках. Поляризация диэлектриков.
Вектор поляризации (поляризованность)
Так как на молекулы диэлектрика во внешнем однородном электрическом поле действуют силы, стремящиеся развернуть их так, чтобы их электрический дипольный момент был направлен по направлению поля, то при определенных условиях может получиться так, что все молекулы диэлектрика сориентируются в поле и их электрические дипольные моменты будут направлены по направлению внешнего электрического поля. На поверхностях диэлектрика в этом случае "появятся" заряды обоих знаков с поверхностной плотностью +s' и -s' (рис. 3.5).
 Процесс "появления" зарядов на диэлектриках во внешнем электрическом поле называют поляризацией диэлектрика. "Появившиеся" заряды называют связанными (поляризационными).
Процесс "появления" зарядов на диэлектриках во внешнем электрическом поле называют поляризацией диэлектрика. "Появившиеся" заряды называют связанными (поляризационными).
Различные вещества поляризуются по-разному в зависимости от их строения. Наиболее часто встречаются следующие виды поляризации диэлектриков:
а) деформационная поляризация – это поляризация диэлектриков, при которой у атомов возникает (индуцируется) дипольный момент за счет деформации электронных орбит. Наблюдается у диэлектриков, состоящих из неполярных молекул у веществ, молекулы которых имеют симметричное строение (N2, H2, O2, CO2, CH4);
б) ориентационная, или дипольная поляризация, которая заключается в ориентации имеющихся дипольных моментов молекул по направлению электрического поля. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрического поля и теплового движения) возникает преимущественная ориентация дипольных моментов по полю. Ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура. Она характерна для диэлектриков, состоящих из полярных молекул веществ, молекулы которых имеют асимметричное строение, т. е. центры "тяжести" положительных и отрицательных зарядов не совпадают. К таким веществам, например, относятся H2O, NH3, SO2, CO;
в) ионная поляризация, которая заключается в смещении подрешетки положительных ионов вдоль поля, а отрицательных ионов - против поля. Смещение подрешеток приводит к возникновению дипольных моментов и ²появлению² на поверхности диэлектрика связанных зарядов. Наблюдается у диэлектриков, имеющих ионную кристаллическую решетку (например, у таких веществ, как NaCl, KCl, KBr).
При помещении диэлектрика во внешнее электрическое поле он поляризуется, т.е. приобретает отличный от нуля электрический дипольный момент:
 , (3.7)
, (3.7)
где pi – дипольный момент одной молекулы.
Для количественной характеристики поляризации диэлектриков вводится в рассмотрение физическая величина, численно равная электрическому дипольному моменту единицы объема диэлектрика:
 . (3.8)
. (3.8)
Эта величина называется вектором поляризации, или поляризованностью. Если поле или диэлектрик однородны, то вектор поляризации одинаков по всему объему. Такую поляризацию называют однородной. Если эти условия не выполняются, то поляризацию называют неоднородной.
У большинства диэлектриков, кроме так называемых сегнетоэлектриков, вектор поляризации пропорционален напряженности внешнего электрического поля:
 , (3.9)
, (3.9)
где c – диэлектрическая восприимчивость вещества, не зависящая от напряженности внешнего электрического поля.
Между вектором поляризации P и поверхностной плотностью связанных зарядов s' имеется связь
 , (3.10)
, (3.10)
т. е. поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации в данной точке поверхности диэлектрика.
При совпадении направления нормальной составляющей вектора поляризации с направлением положительной нормали к поверхности Pn>0 и s'>0, при несовпадении - Pn<0, s'<0.
 Так как
Так как  , а
, а  , то
, то
 , (3.11)
, (3.11)
где En – нормальная составляющая вектора напряженности электричес-кого поля внутри диэлектрика.
Следовательно, там, где линии вектора напряженности электрического поля E выходят из диэлектрика (En>0) - s'>0, где входят в диэлектрик (En<0) - s'<0 (рис. 3.6).
3.3. Поле в диэлектриках. Электрическое смещение.
Диэлектрическая восприимчивость вещества.
Относительная диэлектрическая проницаемость среды. Теорема Остроградского-Гаусса для потока
вектора индукции электрического поля
Электрическим смещением (индукцией электрического поля) называют векторную физическую величину, связанную с вектором поляризации и вектором напряженности электрического поля соотношением
 . (3.12)
. (3.12)
 С учетом того что
С учетом того что  , уравнение (3.12) можно переписать в виде
, уравнение (3.12) можно переписать в виде
 , (3.13)
, (3.13)
где  – относительная диэлектричес-кая проницаемость среды.
– относительная диэлектричес-кая проницаемость среды.
Если в поле, созданное в вакууме бесконечно заряженными плоскостями, внести пластину из однородного диэлектрика так, чтобы её боковые грани были параллельны плоскостям, то на поверхностях пластины "появятся" связанные заряды с поверхностной плотностью s', которые создают свое электрическое поле, направленное в сторону, противоположную внешнему полю (рис. 3.7).
Внутри диэлектрика в этом случае существует результирующее электрическое поле с напряженностью
 , (3.14)
, (3.14)
где  – напряженность внешнего электрического поля;
– напряженность внешнего электрического поля;
 – напряженность электрического поля связанных зарядов.
– напряженность электрического поля связанных зарядов.
Тогда
 . (3.15)
. (3.15)
Вне диэлектрика напряженность внешнего поля равна напряженности результирующего электрического поля.
Так как поле перпендикулярно граням пластины и плоскостям, то En = E, а с учетом того, что  , выражение (3.15) можно переписать так:
, выражение (3.15) можно переписать так:
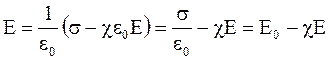 . (3.16)
. (3.16)
Из формулы (3.16) имеем
 ,
,
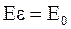 ,
,
 . (3.17)
. (3.17)
Следовательно, относительная диэлектрическая проницаемость среды показывает, во сколько раз электрическое поле ослабевает за счет диэлектрика.
Индукция электрического поля D внутри диэлектрика и вне диэлектрика одинакова, т.к. при умножении  на ee0 имеем
на ee0 имеем
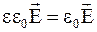 , или
, или  , (3.18)
, (3.18)
где D = ee0E– индукция (электрическое смещение) электрического поля внутри диэлектрика;
Do = e0E – индукция (электрическое смещение) электрического поля вне диэлектрика.
Таким образом, индукция электрического поля в диэлектрике изменяет свое направление, но не изменяет свою величину, в то время как напряженность электрического поля E ¹ E o. Полученный результат справедлив для любых электрических полей.
Следовательно, на границе раздела двух сред происходит изменение вектора напряженности электрического поля E (уменьшается число силовых линий вектора E), а вектор индукции электрического поля не изменяется (изменяется лишь вид силовых линий вектора D). Отсюда вывод: поток вектора индукции электрического поля через любую замкнутую поверхность остается величиной постоянной.
Для потока вектора индукции электрического поля D справедлива теорема Остроградского-Гаусса: поток вектора индукции электрического поля через любую замкнутую поверхность равен алгебраической сумме электрических зарядов, заключенных внутри этой замкнутой поверхности.
Математически эту теорему можно записать так:
 . (3.19)
. (3.19)
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 57; Нарушение авторских прав?; Мы поможем в написании вашей работы!