Соответствия и отношения.

Занятие 3.

Упражнения.

Занятие 2.

Упражнения.

Элементы теории множеств.

Филиал ГОУ ВПО МГУТУ в г. Мелеузе

КУРСОВОЕ И ДИПЛОМНОЕ ПРОЕКТИРОВАНИЕ

Методическое пособие

Редактор: Мельникова Н.В.

________________________________________________________________________

Подписано в печать _____________ Формат 210 297. Печать офсетная.

Усл. печ. л. ____ Уч. – изд. л.____ Тираж _____ экз. Заказ __________

________________________________________________________________________

Московский государственный университет технологий и управления

Адрес: 453850, Башкортостан, Мелеуз, Смоленская, 34

Контрольные вопросы.

1. Приведите примеры конечных и бесконечных множеств.

2. Перечислите способы задания множеств.

3. Назовите несколько подмножеств

а) множества натуральных чисел; б) множества геометрических фигур.

4. Какие множества называются равными? Какие из следующих множеств геометрических фигур на плоскости равны между собой:

A – множество всех квадратов;

B - множество всех прямоугольников;

C - множество всех четырехугольников с прямыми углами;

D - множество всех прямоугольников с равными сторонами;

F - множество всех ромбов с прямыми углами?

5. Перечислите основные операции над множествами. Для каждой операции сформулируйте определение и приведите простые примеры.

1. Запишите множество A, элементами которого являются натуральные делители числа 24, используя перечисление элементов множеств.

2. Даны множества: A={а, и, о, у, э, ы}, B={111, 222, 333, 444, 555, 666, 777, 888, 999}, C={0, 2, 4, 6, 8}. Задайте каждое из них описанием характеристического свойства.

3. Даны числа: 19; ; 0; -27; 5,4 . Какие из них принадлежат множеству: а) целых чисел; б) целых неотрицательных чисел; в) рациональных чисел; г) действительных чисел?

4. Изобразите на координатной прямой множество Х, если

a) Х = {x½xÎR, -2 £ x £ 7};

b) Х = {x½xÎZ, -1 < x < 3};

c) Х = {x½xÎN, -2 < x £ 3}.

5. Изобразите на координатной прямой множество решений неравенства: .

6. Найдите множество решений уравнения, используя формулу для расстояния между двумя точками координатной прямой: а) ; б) .

7. Дано множество A={72, 56, 513, 117, 324}. Составьте подмножества данного множества, состоящие из чисел, которые:

а) делятся на 4;

б) делятся на 9;

в) делятся на 5;

г) не делятся на 10.

8. Изобразите при помощи кругов Эйлера множества P и Q_i, если P – множество равнобедренных треугольников,

а) Q₁ – множество остроугольных треугольников;

б) Q₂ – множество прямоугольных треугольников;

в) Q₃ – множество равносторонних треугольников.

Изобразите все четыре множества на одном чертеже.

9. Пусть A - множество натуральных чисел, запись которых оканчивается 0, B - множество натуральных чисел, кратных 10. Докажите, что множества A и B равны.

10. Известно, что N множество натуральных чисел, Z – множество целых чисел. Докажите, что высказывание Z Ì N - ложно.

11. Изобразите при помощи кругов Эйлера множества A, B и C, если:

а) А - множество четных целых чисел,

B - множество целых чисел, кратных 4;

b) А - множество четных целых чисел,

В - множество целых чисел, кратных 2;

с) А - множество нечетных целых чисел,

В - множество целых чисел, кратных 3,

С - множество чисел, кратных 5.

12. Отношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств.

А D

F

Рис. 1

13. Установите, в каком отношении находятся множества А и В, если А = {a, b, c, d}, а множество В:

а) {k, l, m}; b) {b, c, o, f, k}; с) {b, d}.

Задания для самостоятельной работы.

I. Повторите теоретический материал по теме ²Множества. Операции над множествами². Попытайтесь ответить на контрольные вопросы к занятию 2.

II. Решите задачи:

1. Для каждого из слов “сосна“, “осколок“, “насос“, “колосс“, “сокол“ составьте множество его различных букв. Имеются ли среди полученных множеств равные?

2. Найдите все подмножества множества М = . Сколько подмножеств получилось?

3. В каких отношениях находятся множества решений неравенств:

а) ; б) ?

4. А – множество двузначных чисел, В – множество четных натуральных чисел, С – множество чисел, кратных числу 4. В каком из случаев изображены данные множества? Приведите примеры множеств для двух других случаев.

а) б) в)

5. Задайте множество D, элементами которого являются натуральные числа, меньшие семи.

Контрольные вопросы.

1. Дайте определения: а) пересечения множеств; б) объединения множеств; в) разности двух множеств; г) дополнения множества А до множества В; д) декартова произведения множеств. Как называются соответствующие операции над множествами?

2. Как с помощью кругов Эйлера изобразить а) пересечение множеств; б) объединение множеств; в) разность двух множеств; г) дополнение множества А до множества В?

3. Назовите основные свойства операций пересечения и объединения множеств.

4. Каков порядок действий в формулах, содержащих несколько теоретико-множественных операций, если формулы

а) не содержат скобок; б) содержат скобки?

6. Как изображается на координатной плоскости декартово произведение двух числовых множеств? Приведите примеры.

1. Множество A - множество натуральных чисел, кратных 3, множество B -множество натуральных чисел кратных 7. Задайте множества 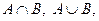выясните, какие из чисел 42, 15, 70, 26, 0 им принадлежат?

2. Множество A - множество натуральных чисел, кратных 3, множество B -множество натуральных чисел кратных 7. Задайте описанием характеристического свойства разность множеств A и B и назовите несколько чисел, принадлежащих этому множеству.

3. Найдите пересечение и объединение множества C={14, 15, 16, 17, 18, 19, 20} и множества D, если

а) D={12, 14, 18, 20, 22, 24};

б) D={14, 16, 18, 20};

в) D={3, 4, 5, 6};

г) D=C.

4. Найдите пересечение и объединение множеств:

а) и ;

б) и ;

в) и .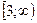

5. Даны множества: A - тупоугольных треугольников, B - прямоугольных треугольников, C - треугольников с углом в 50 градусов. Постройте для данных множеств круги Эйлера и выделите штриховкой множество . Задайте это множество описанием характеристического свойства.

6. Найдите разность множества A={a, b, c, d, e} и множества B, если

а) B={c, d, e, f, k, l};

б) B={a, e, c};

в) B={c, a, d};

г) B={k, l, m};

д) B - пустое множество.

7. Множество A состоит из натуральных чисел от 2 до 10, множество B из натуральных чисел от 5 до 20. Перечислите элементы множеств: А\B, B\A.

8. Найдите дополнение множества четных натуральных чисел до множества натуральных чисел; множества целых чисел до множества рациональных.

9. Множество А - множество двузначных чисел, множество В - множество натуральных чисел, кратных 3, множество С - множество натуральных чисел, кратных 7. Постройте для данных множеств круги Эйлера и выделите штриховкой множества а) АÇ(В\C); b) AÈ(B\C).

10. Множество Е - множество четных чисел, множество F - множество натуральных чисел, кратных 4, множество G - множество натуральных чисел, кратных 7. Постройте для данных множеств круги Эйлера и выделите штриховкой множества а) (Е \ F) Ç G; b) (Е \ F) È G.

11. Изобразите на координатной плоскости элементы декартова произведения множеств: A={1, 2, 3, 4} и B={4,5}.

12. На координатной плоскости постройте фигуру, все точки которой являются элементами декартова произведения множеств A=R и B=[2;5].

Задание для самостоятельной работы.

I. Повторите теоретический материал по темам ²Множества. Операции над множествами², ²Соответствия и отношения². Попытайтесь ответить на контрольные вопросы к занятию 3.

II. Решите задачи:

1. Даны множества А = {8; 5; 3; 2; 0} и В = {5; 1; 4; 2 }. Запишите множества АÈВ, АÇВ, А\В, В\А.

2. Множество А - множество натуральных чисел, кратных 3, множество В - множество натуральных чисел, кратных 5, множество С - множество натуральных чисел, кратных 7. Постройте для данных множеств круги Эйлера и выделите штриховкой множества а) АÇ(ВÈС); b) АÈ(ВÇС).

3. Перечислите элементы, принадлежащие множеству 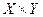, если:

а) X={a, b, c}, Y={k,l};

б) X={a, b, c}, Y -пустое множество.

4. Используя цифры 2, 7, 5, 4 запишите все возможные трехзначные числа (цифры в записи числа не повторяются). Сколько кортежей длины 3 получили?

5. На координатной плоскости изобразите декартовы произведения множеств:

а) М = {2; 4; 7; 8} и N = {-1; 0; 4; 5; 6};

b) M = [2;5] и N = {1; 3; 4};

c) M = [3;7] и N = [2; 5].

Контрольные вопросы.

1. Дайте определение соответствия между множествами X и Y. Приведите примеры соответствий.

2. Назовите способы задания соответствий.

3. Что такое граф соответствия; график соответствия?

4. Дайте определение обратного соответствия.

5. Какое соответствие называется взаимно однозначным?

6. Какие множества называются равномощными? Приведите примеры равномощных множеств.

7. Дайте определение бинарного отношения на множестве Х. Приведите примеры отношений.

8. В чем состоит свойство

а) рефлексивности;

б) симметричности;

в) антисимметричности;

г) транзитивности;

д) связанности

отношения? Какова особенность графа отношения в каждом из случаев?

9. Дайте определения отношений эквивалентности и порядка. Приведите примеры таких отношений.

Дата добавления: 2017-02-01