Элементы математической логики.

Занятие 5.

Упражнения.

Элементы математической логики.

Занятия 4.

Контрольные вопросы.

1. Что такое понятие, объем понятия, содержание понятия? В чем особенность математических понятий?

2. В чем состоит отношение рода и вида для понятий? Приведите примеры понятий, находящихся в отношении рода и вида

а) из области математики;

б) из области языковых дисциплин;

в) из других дисциплин.

3. Приведите структуру явного определения понятия; примеры явных определений.

4. Дайте определение высказывания. Приведите примеры истинных и ложных высказываний и примеры предложений, не являющихся высказываниями.

5. Что называется одноместной высказывательной формой? n-местной высказывательной формой? Приведите примеры высказывательных форм. Дайте определение множества истинности высказывательной формы.

6. Как определяется конъюнкция высказываний? Составьте таблицу истинности конъюнкции.

7. Что такое конъюнкция высказывательных форм? Как найти множество истинности конъюнкции двух высказывательных форм А(х) и В(х)?

8. Дайте определение дизъюнкции высказываний. Составьте таблицу истинности дизъюнкции.

9. Сформулируйте определение дизъюнкции высказывательных форм. Как определить множество истинности дизъюнкции двух высказывательных форм А(х) и В(х)?

10. Как определяется отрицание высказываний и высказывательных форм? Приведите примеры отрицаний.

1. Находятся ли в отношении рода и вида следующие пары понятий:

а) многоугольник и треугольник;

б) угол и острый угол;

в) луч и прямая;

г) ромб и квадрат;

д) круг и окружность?

2. Изобразите при помощи кругов Эйлера отношение между объемами понятий a, b и c, если:

а) а - ²четырехугольник²;

b - ²трапеция²;

с - ²прямоугольник²;

б) а - ²натуральное число, кратное 3²;

b - ² натуральное число, кратное 4²;

с - ²натуральное число².

3. В следующих определениях выделите определяемое и определяющее понятия; родовое понятие (по отношению к определяемому) и видовое отличие:

а) параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны;

б) отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

4. Какие из следующих предложений являются высказываниями, а какие высказывательными формами:

а) 3x+2=4;

б) существует х такое, что ;

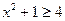в) (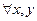) x+y=y+x;

г) y=5 является решением уравнения y-4=1.

5. Среди приведенных ниже предложений найдите высказывания и установите их значения истинности:

а) (15+3)*(6-4) = 36;

б) ;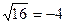

в) число 4,7ÎN;

г) в любом прямоугольнике противоположные стороны равны;

д) (14+х) = 34;

е) число z – трехзначное;

ж) четное число – это число, которое делится на 2.

6. Какие предложения из задания № 1 являются высказывательными формами? Подставьте в них вместо переменной значение так, чтобы получилось а) истинное; б) ложное высказывание. Найдите множество истинности для каждой высказывательной формы.

7. Можно ли считать высказывательными формами записи:

а) х² – 2х; б) 4х + 2y;

в) число 3 является корнем уравнения х² – 9 = 0?

8. Обозначьте элементы высказываний буквами и запишите следующие высказывания с помощью символов логики:

-в параллелограмме ABCD угол A прямой и диагонали взаимно перпендикулярны;

-число 12 двузначное и кратно 2 или трем.

9. Найдите значения истинности следующих высказываний и дайте соответствующие пояснения: а) 15 кратно 3 и 12 кратно3; б) 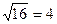или 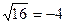; в) 5 ³ 3; г) х = 2 является корнем уравнения х² = 9 или решением неравенства 2х – 1 < 3; д) –2 < 3 < 1/

10. Даны высказывания:

A: “Сегодня ясно”;

B: “Сегодня идет дождь”;

C: “Сегодня идет снег”;

D: “Я пойду в гости”.

Сформулируйте следующие высказывания:

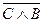1) A Ù ; 2) ; 3) .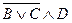

11. Являются ли следующие высказывания отрицанием друг друга:

а)Число 253- простое. Число 253- составное.

б) Угол 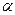- тупой. Угол 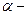острый.

12.Сформулируйте, используя законы де Моргана, отрицания следующих утверждений:

а) Четырехугольник ABCD – прямоугольник или параллелограмм.

б) Число 14 – четное и делится на 3.

13. Найдите множества истинности высказывательных форм P(x): “x² – 4 = 0” и Q(x): “3x – 2 < 17”, если их область определения есть: 1) R; 2) N.

14. На множестве М = {1, 2, …, 20} заданы высказывательные формы: А(x): “x не делится на 5”, В(х): “х - четное”, С(х): “х - простое”, D(x): “х делится на 3”. Найти множества истинности следующих высказывательных форм:

а)

б)

в)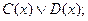

г)

д)

15. Выясните, какие из высказывательных форм являются тождественно истинными:

а) х² + у² ³ 0;

б) х² + 1 ³ (х + 1)²;

в) sin²x + cos²x = 1;

г) (х + 1)² > х – 1.

Задание для самостоятельной работы.

I. Повторите теоретический материал по теме ²Понятия. Высказывания и высказывательные формы. Конъюнкция и дизъюнкция. Отрицание высказываний. Высказывания с кванторами. Импликация и эквиваленция.² Попробуйте ответить на контрольные вопросы к занятию № 5.

II. Решите задачи:

1. Дайте определения: тупоугольного треугольника, равнобедренного треугольника, трапеции. Какие понятия вы выбрали в качестве родового в каждом случае? Какие свойства включили в видовое отличие?

2. Среди следующих предложений укажите высказывания и высказывательные формы и поясните ответ:

а) 4 - натуральное число;

б) разность чисел 16 и 11 равна 7;

в) 2³² > 3¹²;

г) х = 7 является решением неравенства 2х –8 < 9;

д) разность чисел х и 4 равна 17;

е) прямые перпендикулярны;

ж) график функции y = x² симметричен относительно оси ординат.

3. Найдите множество истинности высказывательной формы 2х – 10 < 0, заданной на множестве Х, если

а) X = R; б) Х = N; в) X = {0, 1, 2, 3, 4, 5, 6, 7}

4. Среди следующих предложений укажите составные; выделите в них элементарные предложения и логические связки: а) или 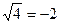; б) противоположные стороны параллелограмма равны и параллельны; в) число делится на 3 тогда и только тогда, когда сумма цифр в его десятичной записи делится на 3; г) число 11 простое и не делится на 3; д) если число делится на 6, то оно делится на 2.

5. По окончании учебного года Лена сказала подругам, что осенью она начнет заниматься в хореографическом кружке и поступит на курсы французского или испанского языков. В сентябре, когда подруги встретились, оказалось, что Лена не занимается в хореографическом кружке, но зато изучает оба языка. Выполнила ли Лена свое обещание? Если вы считаете, что нет, то перечислите все возможные случаи, в которых высказывание Лены было бы истинным.

6. На множестве М = {1, 2, …, 20} заданы высказывательные формы: А(x): “x не делится на 5”, В(х): “х - четное”, С(х): “х - простое”, D(x): “х делится на 3”. Найдите множества истинности следующих высказывательных форм:

а)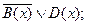

б)

в)

г)

д)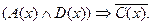

7. На множестве треугольников плоскости заданы высказывательные формы А(х): ²треугольник х прямоугольный² и В(х): ²треугольник х равнобедренный².

Образуйте конъюнкцию и дизъюнкцию этих форм и начертите по 2 фигуры, принадлежащие множеству истинности а) конъюнкции; б) дизъюнкции.

Контрольные вопросы.

1. Приведите примеры высказываний с кванторами.

2. Высказывания какого вида называются кванторами общности (кванторами существования)?

3. Как построить отрицание высказывания с квантором общности (существования)?

4. Как обосновать

а) истинность высказывания с квантором общности;

б) ложность высказывания с квантором общности;

в) истинность высказывания с квантором существования;

г) ложность высказывания с квантором существования?

5. Дайте определение импликации двух высказываний. Приведите таблицу истинности импликации.

6. Как определяется эквиваленция двух высказываний? Какой вид имеет таблица истинности эквиваленции?

7. Что называется отношением логического следования? Приведите примеры отношений логического следования.

8. Дайте определение отношения равносильности. Приведите примеры отношений равносильности.

9. Как связаны множества истинности высказывательных форм А(х) и В(х), если

а) А(х) Þ В(х);

б) А(х) Û В(х)?

Упражнения

1. Запишите, используя символы, следующие высказывания и определите их значения истинности:

а) Всякое число, умноженное на нуль, есть нуль.

б) Произведение любого числа и единицы есть это число.

в) При делении нуля на любое другое число получается нуль.

г) Квадрат любого числа неотрицателен.

2. Укажите способы установления значения истинности высказываний, содержащих кванторы, заполнив таблицу:

Структура высказывания   Значение истинности	("хÎХ)А(х)	($хÎХ)½А(х)
И
Л

3. Докажите или опровергните следующие высказывания:

а) Существуют уравнения, множество решений которых пусто.

б) Всякое целое число является натуральным.

в) Сумма любых двух четных чисел есть число четное.

г) хотя бы одно натуральное число является решением уравнения

7: х =2.

4. Выявите логическую структуру, определите значение истинности и постройте отрицания следующих высказываний:

а) Некоторые нечетные числа делятся на 5.

б) Хотя бы одно из чисел первого десятка составное.

в) Произведение двух любых последовательных натуральных чисел составное.

5. Предложения А(х) и В(х) заданы на множестве натуральных чисел. Следует ли из предложения А(х) предложение В(х), если В(х) - ²Число х - четное², и

а) А(х) - ²Число х делится на 6²;

б) А(х) - ²Число х делится на 7²;

в) А(х) - ²число х делится на 2²?

6.Установите, находятся ли данные пары предложений в отношении следования:

а) Треугольник АВС – равносторонний.

Треугольник АВС – равнобедренный.

б) Четырехугольник АВСD – квадрат.

Четырехугольник АВСD – ромб.

в) х делится на 3 и х делится на 6.

г) а > 2 и a > 5.

7. Среди следующих предложений установите истинные; ответы обоснуйте:

а) Если студент А сдаст все экзамены в сессию без троек, то он будет получать стипендию.

б) Число 15а натуральное, следовательно, а - натуральное число.

в) Если в четырехугольнике все углы прямые, то этот четырехугольник - прямоугольник.

г) Если в четырехугольнике диагонали равны, то это четырехугольник - прямоугольник.

д) Для того, чтобы четырехугольник был прямоугольником, достаточно, чтобы все его углы были равны.

е) Для того, чтобы четырехугольник был прямоугольником, необходимо, чтобы все его углы были равны.

8. Для ложных высказываний из задания 7 постройте отрицания различными способами.

9. Вставьте слова ²и² либо ²или² так, чтобы следующие высказывания были истинными:

а) а*b = 0 Û a = 0... b = 0;

б) a*b ¹ 0 Û a ¹ 0... b ¹ 0;

в) xÎ A Ç B Û x Î A... x Î B;

г) x Ï A Ç B Û x Ï A... x Ï B

10. С помощью таблиц истинности найти значение формулы:

а) A= ;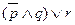

б) B=() .

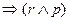11. Семья, состоящая из отца А, матери В и трех дочерей Д₁, Д₂ и Д₃ купила телевизор. Условились, что в первый вечер будут смотреть передачи в таком порядке:

1) Когда отец А смотрит передачу, то мать В делает то же;

2) Дочери Д₂ и Д₃ обе или одна из них смотрят передачу;

3) Из двух членов семьи – мать В и дочь Д₁ – смотрит передачу одна и только одна;

4) Дочери Д₁ и Д₂ или обе смотрят или обе не смотрят;

5) Если дочь Д₃ смотрит передачу, то отец А и дочь Д₂ делают то же.

Кто из членов семьи в этот вечер смотрит телевизор.

12. Приведите примеры таких значений а, для которых данное высказывание истинно:

а)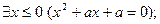

б)

13. Пусть высказывательная форма Q(x): “х делится на у ” определена на множестве N´N. Покажите, что высказывания 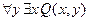и 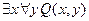имеют различные логические значения.

14. Решите задачу: В городе совершено преступление. Подозреваемые: Джонс, Смит и Браун. Один из них – уважаемый старик, другой – мошенник, а третий – мелкий чиновник. Результаты допроса:

Браун: «Я совершил это, Джонс не виноват»;

Джонс: «Браун не виноват, преступление совершил Смит»;

Смит: «Я не виноват, виноват Браун»

Кто есть кто и кто преступник, если известно, что старик сказал правду, мошенник оба раза соврал, а чиновник один раз солгал и один раз сказал правду, а преступник один.

15. Даны высказывательные формы Р(х): “x² + x + 1 > 0” и Q(x):“x² – 4x + 3 = 0”, определенные на R. Установите, какие из следующих высказываний истинны, а какие ложны:

а)

б)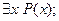

в)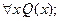

г)

Задание для самостоятельной работы.

I. Повторите теоретический материал по всем изученным темам.

II. Решите задачи:

1. Сформулируйте отрицания следующих высказываний:

а) на каждом курсе есть несколько отличников;

б) хотя бы на одном курсе есть хотя бы один отличник;

в) хотя бы на одном курсе все студенты отличники.

2. Докажите или опровергните следующие утверждения:

а) разность любых двух натуральных чисел есть число натуральное;

б) сумма любых трех последовательных чисел кратна трем;

в) в некоторых параллелограммах диагонали не равны;

г) среди чисел 12, 15, 17, 27, 212 найдется хотя бы одно, кратное 7;

д) любое действительное число является решением уравнения

2(х-3) = 2х - 6.

3. Пусть Р(х): ²треугольник х равносторонний², Q(x): ² треугольник х равнобедренный², R(x): ²треугольник х прямоугольный². Сформулируйте следующие высказывания и установите их значения истинности:

а) ("х) Р(х); б) ($х) Р(х); в) ($х) Р(х) Ù R(x);

г) ($х) R(x) Ù Q(x).

4. С помощью таблиц истинности найти значение формулы:

C= .

5. На судебном процессе адвокат сделал следующее заявление: “Если Джонс – убийца, то ему известно время смерти и чем был убит Смит. Поэтому, если Джонс не знает, когда умер Смит, или не знает, чем Смита убили, то он не убийца”. Прав ли адвокат?

Дата добавления: 2017-02-01