
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент эластичности
|
|
|
|
РЕГРЕССИЯ
- зависимость среднего значения какой-либо случайной величины от нек-рой другой величины или от нескольких величин. Если, например, при каждом значении х=xi наблюдается ni значений  случайной величины Y, то зависимость средних арифметических
случайной величины Y, то зависимость средних арифметических
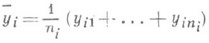
этих значений от xi и является Р. в статистич. понимании этого термина. При обнаруженной закономерности изменения 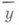 с изменением хпредполагается, что в основе наблюдаемого явления лежит вероятностная зависимость: при каждом фиксированном значении хслучайная величина Y имеет определенное распределение вероятностей с математич. ожиданием, к-рое является функцией х:
с изменением хпредполагается, что в основе наблюдаемого явления лежит вероятностная зависимость: при каждом фиксированном значении хслучайная величина Y имеет определенное распределение вероятностей с математич. ожиданием, к-рое является функцией х: 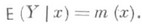
Зависимость 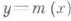 , где хиграет роль "независимой" переменной, наз. р е г р е с с и е й (или ф у н к ц ие й р е г р е с с и и) в вероятностном понимании этого термина. График функции т(х)наз. л и н и е й р ег р е с с и и, или к р и в о й р е г р е с с и и, величины Y по х. Переменная хназ. р е г р е с с и о н н о й п е р е м е н н о й, или р е г р е с с о р о м. Точность, с к-рой линия регрессии Yпо хпередает изменение Yв среднем при изменении х, измеряется дисперсией величины Y, вычисляемой для каждого значения х:
, где хиграет роль "независимой" переменной, наз. р е г р е с с и е й (или ф у н к ц ие й р е г р е с с и и) в вероятностном понимании этого термина. График функции т(х)наз. л и н и е й р ег р е с с и и, или к р и в о й р е г р е с с и и, величины Y по х. Переменная хназ. р е г р е с с и о н н о й п е р е м е н н о й, или р е г р е с с о р о м. Точность, с к-рой линия регрессии Yпо хпередает изменение Yв среднем при изменении х, измеряется дисперсией величины Y, вычисляемой для каждого значения х:
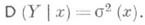
Графически зависимость дисперсии s2 (х)от хвыражается т. н. с к е д а с т и ч е с к о й л и н и е й. Если s2 (х)=0при всех значениях x, то с вероятностью 1 величины связаны строгой функциональной зависимостью. Если s2 (х)№0ни при каком значении хи т (х)не зависит от х, то регрессия Yпо хотсутствует..
В теории вероятностей задача Р. решается применительно к такой ситуации, когда значения регрессионной переменной х соответствуют значениям нек-рой случайной величины Xи предполагается известным совместное распределение вероятностей величин Xи Y(при этом математич. ожидание 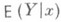 и дисперсия
и дисперсия 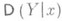 будут соответственно условным математич. ожиданием и условной дисперсией случайной величины Yпри фиксированном значении X=x). В этом случае определены две Р.: Y по х и X по у, и понятие Р. может быть использовано также для того, чтобы ввести нек-рые меры взаимосвязанности случайных величин X и Y, определяемые как характеристики степени концентрации распределения около линий Р. (см. Корреляция).
будут соответственно условным математич. ожиданием и условной дисперсией случайной величины Yпри фиксированном значении X=x). В этом случае определены две Р.: Y по х и X по у, и понятие Р. может быть использовано также для того, чтобы ввести нек-рые меры взаимосвязанности случайных величин X и Y, определяемые как характеристики степени концентрации распределения около линий Р. (см. Корреляция).
Функции Р. обладают тем свойством, что среди всех действительных функций f(x)минимум математич. ожидания 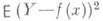 достигается для функции f(x) = т (х), то есть регрессия Y по хдает наилучшее (в указанном смысле) представление величины Y. Наиболее важным является тот случай, когда регрессия Y по хл и н е й н а, т. е.
достигается для функции f(x) = т (х), то есть регрессия Y по хдает наилучшее (в указанном смысле) представление величины Y. Наиболее важным является тот случай, когда регрессия Y по хл и н е й н а, т. е.
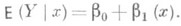
Коэффициенты b0 и b1, наз. коэффициентами Р., легко вычисляются:
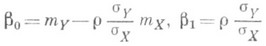
(здесь r - корреляции коэффициент X и Y,  ,
,
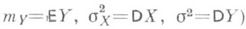 , и п р я м а я регрессии Y по х имеет вид
, и п р я м а я регрессии Y по х имеет вид
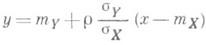
(аналогичным образом находится прямая регрессии Xпо у). Точная линейная Р. имеет место в случае, когда двумерное распределение величин Xи Y является нормальным.
В условиях статистич. приложений, когда для точного определения Р. нет достаточных сведений о форме совместного распределения вероятностей, возникает задача приближенного нахождения Р. Решению этой задачи может служить выбор из всех функций g(x), принадлежащих заданному классу, такой функции, к-рая дает наилучшее представление величины Y в том смысле, что минимизирует математич. ожидание 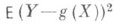 . Найденная функция наз. с р е д н е й к в а д р а т и ч е с к о й Р.
. Найденная функция наз. с р е д н е й к в а д р а т и ч е с к о й Р.
Простейшим будет случай л и н е й н о й с р е д н е й к в а д р а т и ч е с к о й Р., когда отыскивают наилучшую линейную аппроксимацию величины Y посредством величины X, т. е. такую линейную функцию
 , для к-рой выражение
, для к-рой выражение 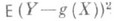
принимает наименьшее возможное значение. Данная экстремальная задача имеет единственное решение
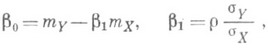
т. е. вычисление приближенной линии Р. приводит к тому же результату, к-рый получен в случае точной линейной Р.:
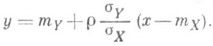
Минимальное значение 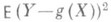 при вычисленных значениях параметров равно
при вычисленных значениях параметров равно 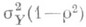 . Если регрессия т(х)существует, то при любых b0 и b1 имеет место соотношение
. Если регрессия т(х)существует, то при любых b0 и b1 имеет место соотношение
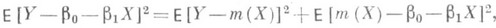
откуда следует, что прямая средней квадратич. регрессии 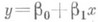 дает наилучшее приближение к линии регрессии т(х), если измерять расстояние вдоль оси у. Поэтому если линия т(х)есть прямая, то она совпадает с прямой средней квадратической Р.
дает наилучшее приближение к линии регрессии т(х), если измерять расстояние вдоль оси у. Поэтому если линия т(х)есть прямая, то она совпадает с прямой средней квадратической Р.
В общем случае, когда Р. сильно отличается от линейной, можно поставить задачу нахождения многочлена 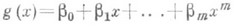 нек-рой степени т, для к-рого среднее значение
нек-рой степени т, для к-рого среднее значение  имеет возможно меньшее значение.
имеет возможно меньшее значение.
Такое решение задачи соответствует п а р а б о л ич е с к о й (или п о л и н о м и а л ь н о й) средней квадратической Р. (см. Параболическая регрессия).порядка т. Кривая 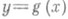 есть парабола m-го порядка, дающая наилучшую аппроксимацию истинной линии Р. Обобщением параболической Р. служит функция Р., выраженная линейной комбинацией тех или иных заданных функций:
есть парабола m-го порядка, дающая наилучшую аппроксимацию истинной линии Р. Обобщением параболической Р. служит функция Р., выраженная линейной комбинацией тех или иных заданных функций:
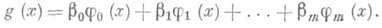
Наиболее важное значение имеет случай, когда j0 (х), ..., j m (х) - ортогональные многочлены соответствующих порядков, построенные по распределению X. Другими примерами н е л и н е й н о й (к р и в о л ин е й н о й) Р. являются случаи тригонометрической Р., показательной Р., и т. п.
Понятие Р. естественным образом обобщается на тот случай, когда вместо одной регрессионной переменной рассматривается нек-рое множество переменных. Если случайные величины X1 Х 2, ..., Х п имеют совместное распределение вероятностей, то множественная Р. определяется, напр., как регрессия X1 по x2 ,..., х п:
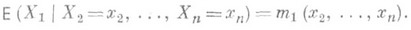
Соответствующее уравнение определяет поверхность регрессии Х 1 по х 2 ,..., х n. Линейная регрессия Х 1 по х 2 ,..., х п имеет вид
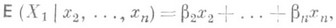
где b2,..., b n - коэффициенты Р. (при 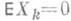 ). Линейная средняя квадратическая Р. величины Х 1 по x2,..., х п определяется как наилучшая линейная оценка величины Х 1 величинами Х 2 ,..., Х п в смысле обращения в минимум выражения
). Линейная средняя квадратическая Р. величины Х 1 по x2,..., х п определяется как наилучшая линейная оценка величины Х 1 величинами Х 2 ,..., Х п в смысле обращения в минимум выражения

Соответствующая п л о с к о с т ь Р. дает наилучшую аппроксимацию поверхности регрессии x1=m(x2,..., х п), если последняя существует. Если поверхность Р. есть плоскость, то она необходимо совпадает с плоскостью средней квадратической Р. (так будет в случае, когда совместное распределение всех пвеличин нормально).
Простым примером регрессии Yпо Xявляется зависимость между Yи X, к-рая выражается соотношением 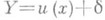 , где
, где 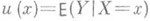 , а случайные величины Xи dнезависимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи у=и (х)между неслучайными величинами уи х. Эта же модель Р. используется во многих приложениях при изучении характера зависимости случайной величины Yот неслучайной величины х. На практике выбор функции у=и (х)и оценку неизвестных коэффициентов Р. по экспериментальным данным производят методами регрессионного анализа.
, а случайные величины Xи dнезависимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи у=и (х)между неслучайными величинами уи х. Эта же модель Р. используется во многих приложениях при изучении характера зависимости случайной величины Yот неслучайной величины х. На практике выбор функции у=и (х)и оценку неизвестных коэффициентов Р. по экспериментальным данным производят методами регрессионного анализа.
Лит.:[1] К р а м е р Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; [2] К е н д а л л М. Д ж., С т ь ю а р т А., Статистические выводы и связи, пер. с англ., М., 1973. А. <В. Прохоров.
Корреляция
КОРРЕЛЯЦИЯ [correlation] — величина, характеризующая взаимную зависимость двух случайных величин, X и Y, безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной К.). Для того чтобы определить эту зависимость, рассмотрим новую случайную величину — произведение отклонения значений x от его среднего Mx и отклонения y от своего среднего My. Можно вычислить среднее значение новой случайной величины:
rxy = M {(x – Mx) (y – My)}.
Это среднее получило название корреляционной функции, или ковариации. На ее основе (делением на корень из произведения дисперсий σ2x, σ2y, т. е. на произведение стандартных отклонений) строится коэффициент К.:
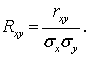
При нелинейной зависимости аналогичный показатель носит название индекса К.
Если x и y независимы, то Rxy = 0. Если же x и y зависимы, то обычно Rxy ≠ 0. Причем в тех случаях, когда зависимость полная, то либо Rxy = 1 (x и y растут или уменьшаются одновременно), либо Rxy = –1 (при увеличении одной из них другая уменьшается). Следовательно, коэффициент К. может изменяться от –1 до +1.
К. используется для выявления статистической зависимости величин при обработке данных. Наряду с указанной формулой используется ряд формул эмпирического определения тесноты корреляционной связи между наблюдаемыми признаками исследуемых величин
Анцупов А.Я., Шипилов А.И. Словарь конфликтолога, 2009 г.
ДЕТЕРМИНАЦИЯ – взаимозависимость и взаимовлияние систем. Любая общественная система функционирует, взаимодействуя не только с природой, но и с др. социальными системами, которые образуют по отношению к ней внешнюю историческую среду. Каждая социальная система, будучи частью (элементом) мирового сообщества, детерминируется этим целым, оказывая на него, в свою очередь, обратное воздействие. Влияние внешней исторической среды на развитие общества выражается, в частности, в действии закона исторической корреляции. Роль различных факторов в системе Д. конфликта не является одинаковой: если одни детерминанты определяют его возникновение, функционирование и развитие, то др. лишь влияют на него. Соответственно все детерминирующие факторы конфликта наиболее общим образом можно определить как главные и неглавные (второстепенные). Выделяются два основных уровня Д.: «сущностный» и «феноменологический». Первый характеризуется действием главных факторов, которые определяют природу конфликта, его существенные, необходимые стороны; а второй – действием второстепенных факторов, которые, определяя единичные черты конфликта, придают ему неповторимый и своеобразный вид. Довольно удачным вариантом типологии видов Д. является предложенная Я. Аскиным классификация на основе временных отношений. Соответственно временным модусам (прошлое, настоящее и будущее) выделяются три основных типа Д.: Д. из прошлого, из настоящего и из будущего, которые могут выступать как в материальной, так и в идеальной формах. Д. прошлым представлена, как причинность, условия и связь состояний; Д. настоящим – функциональная зависимость, корреляция, системная Д.; Д. будущим – Д. целью, зачатки будущего в явлении.
Как и в экономической теории и ряде других дисциплинах в эконометрике есть понятие среднего коэффициента эластичности Э – который показывает, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины:
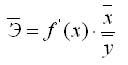
Аппроксима́ция, или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.
Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.
В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сереном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»
· Для приближенного вычисления интеграла используется формула прямоугольников или формула трапеций, или более сложная квадратурная формула. Фактически при этом происходит приближение подинтегральной функции ступенчатой функцией или вписанной ломаной, интеграл от которой считается мгновенно.
· Для вычисления значений сложных функций часто используется вычисление значения отрезка ряда, аппроксимирующего функцию.
· Для обработки экспериментальных или натурных данных. Тут следует рассматривать два случая: 1) аппроксимирующая функция ограничена диапазоном заданных точек и служит в качестве только интерполирующей зависимости; 2) аппроксимирующая функция выступает в роли физического закона и с ее помощью допускается экстраполировать переменные. Приведем пример. Пусть на основе натурных наблюдений получены следующие пары чисел x и y (см. запись в блоге Г. Александрова[ неавторитетный источник? ]):

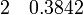
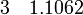
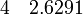
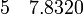
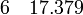
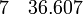
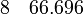
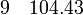
Если функция будет использована только для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:
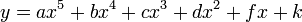
где:
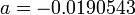
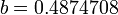
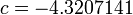
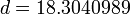
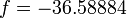
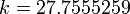
Намного сложней обстоит дело в случае, если приведенные выше натурные данные служат опорными точками для выявления закона изменения y=F(x) с известными граничными условиями. Например: F(0)=0 и 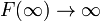 . Тут уже качество результата зависит от профессионализма исследователя. В данном случае наиболее приемлемым окажется закон:
. Тут уже качество результата зависит от профессионализма исследователя. В данном случае наиболее приемлемым окажется закон:
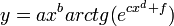
где:
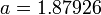
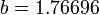
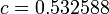
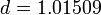
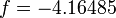
Для оптимального подбора параметров уравнений обычно используют метод среднеквадратичных отклонений
Аппроксима́ция, или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.
Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.
В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сереном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»
· Для приближенного вычисления интеграла используется формула прямоугольников или формула трапеций, или более сложная квадратурная формула. Фактически при этом происходит приближение подинтегральной функции ступенчатой функцией или вписанной ломаной, интеграл от которой считается мгновенно.
· Для вычисления значений сложных функций часто используется вычисление значения отрезка ряда, аппроксимирующего функцию.
· Для обработки экспериментальных или натурных данных. Тут следует рассматривать два случая: 1) аппроксимирующая функция ограничена диапазоном заданных точек и служит в качестве только интерполирующей зависимости; 2) аппроксимирующая функция выступает в роли физического закона и с ее помощью допускается экстраполировать переменные. Приведем пример. Пусть на основе натурных наблюдений получены следующие пары чисел x и y (см. запись в блоге Г. Александрова[ неавторитетный источник? ]):

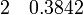
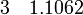
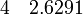
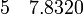
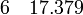
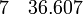
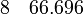
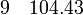
Если функция будет использована только для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:
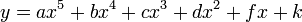
где:
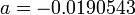
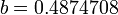
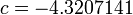
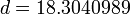
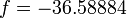
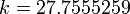
Намного сложней обстоит дело в случае, если приведенные выше натурные данные служат опорными точками для выявления закона изменения y=F(x) с известными граничными условиями. Например: F(0)=0 и 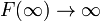 . Тут уже качество результата зависит от профессионализма исследователя. В данном случае наиболее приемлемым окажется закон:
. Тут уже качество результата зависит от профессионализма исследователя. В данном случае наиболее приемлемым окажется закон:
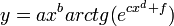
где:
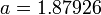
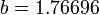
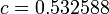
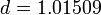
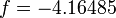
Для оптимального подбора параметров уравнений обычно используют метод среднеквадратичных отклонений
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 95; Нарушение авторских прав?; Мы поможем в написании вашей работы!