Кинетика химических процессов

Измерение ЭДС

Измерить ЭДС любого гальванического элемента с помощью обычного вольтметра нельзя, так как последний показывает не ЭДС элемента, а падение напряжения, зависящее от сопротивления вольтметра. Точное измерение ЭДС гальванического элемента должно проводиться при минимальном прохождении тока, то есть компенсационным методом. Сущность компенсационного метода измерения заключается в том, что к испытуемому элементу, ЭДС которого определяется, присоединяют другой элемент (батарею или аккумулятор) с известной противоположно направленной ЭДС, в результате чего происходит взаимная компенсация ЭДС элементов.

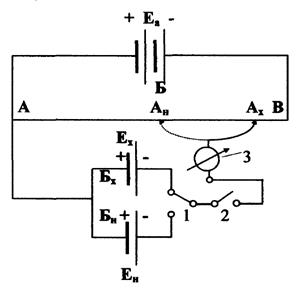
Приборы, в которых используется принцип компенсации, называется потенциометрами. Принципиальная схема потенциометра представлена на рис. 12. Аккумулятор (Е_а»2В) присоединен к концам калиброванной константановой проволоки (реохорда) АВ. Цепь АБВ называется главной. Между клеммой А и гальванометром 3 переключателем 1 включается испытуемый гальванический элемент, ЭДС которого Е_х . ЭДС испытуемого элемента должна быть меньше ЭДС аккумулятора. Для кратковременных включений служит ключ 2. Цепь АБ_х (АБ_н) называется боковой.

Передвижением контакта А_х вдоль реохорда подбирают такое положение, при котором ток в боковой цепи практически отсутствует. Точку компенсации проверяют передвижением контакта влево и вправо от нее по реохорду на 1 мм; при этом стрелка гальванометра должна отклоняться от нулевого положения на одинаковую величину. Достигнутая компенсация означает, что падение напряжения испытуемого элемента, соответствующее его ЭДС, равно падению напряжения аккумулятора на участке АА_х.

Зная длину участка АА_х, длину всего реохорда АВ и ЭДС аккумулятора Е_а, можно определить ЭДС испытуемого элемента:

(3.59)

Точное измерение Е_х затруднено, так как ЭДС аккумулятора изменяется. Поэтому в боковую цепь параллельно с испытуемым элементом включают внешний стандарт - нормальный элемент Вестона, ЭДС которого Е_н точно известна и отличается большой устойчивостью. Элемент Вестона состоит из кадмиевого амальгамного электрода I рода и ртутносульфатного электрода II рода, погруженных в насыщенный раствор сульфата кадмия (рис. 13):

(-) Cd (Hg) ïCdSO₄ ïHg₂SO₄, Hg (+)

Величина Е_н зависит только от температуры и может быть рассчитана следующим образом:

E_н = 1,0186 – 4,06×10^-5(t- 20)(3.60)

где t – температура в °С

Компенсируя ЭДС нормального элемента, находят длину отрезка реохорда АА_н, на котором падение напряжения аккумулятора равно ЭДС нормального элемента. Тогда

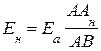. (3.61)

Разделив уравнение (3.59) на (3.61) получаем окончательное выражение, не содержащее неопределенную величину ЭДС аккумулятора:

. (3.62)

Измерение и вычисление ЭДС гальванических элементов значительно упрощается, если исследования проводить при помощи компактных потенциометров различных марок.

Альтернативным методом измерения ЭДС является использование приборов, называемых иономерами. Они представляют собой высокоточные вольтметры с огромным внутренним сопротивлением (для большинства моделей характерно сопротивление 1×10¹² Ом). В отличие от обычных вольтметров, ток, протекающий в цепи, в этом случае будет пренебрежимо малым. Это позволяет достичь приемлемой для большинства задач точности измерения ЭДС на уровне 1 мВ.

Решение типовых задач

Задача 1.

На основании данных об удельном сопротивлении водных растворов угольной кислоты проверить, подчиняется ли данный электролит закону разбавления Оствальда, определить, при какой концентрации степень диссоциации H₂CO₃ в растворе равна 0,05 и чему равен рН этого раствора. Диссоциацией угольной кислоты по второй ступени пренебречь.

С, моль/л	0,1	0,05	0,03	0,01	0,005	0,003	0,001
r, Ом×м

Решение. Найдем удельную электрическую проводимость растворов как обратную величину удельного сопротивления

.

Рассчитаем молярную электрическую проводимость, степень диссоциации и константу диссоциации угольной кислоты по уравнениям (3.15), (3.19) и (3.2) соответственно. Необходимую для расчетов величину молярной электрической проводимости при бесконечном разбавлении находим по закону независимого движения ионов Кольрауша (3.18) на основе справочных данных о предельных подвижностях ионов H⁺ и HCO₃^-, образующихся при диссоциации угольной кислоты.

Результаты вычислений сводим в таблицу:

С, моль/л	0,1	0,05	0,03	0,01	0,005	0,003	0,001
c, См/м	0,00870	0,00610	0,00472	0,00270	0,00196	0,00152	0,000854
l, См×м^2/кмоль	0,087	0,122	0,157	0,270	0,391	0,505	0,854
a	0,00213	0,00299	0,00385	0,00662	0,00959	0,0124	0,0209
Кд×10^7, моль/л	4,55	4,48	4,47	4,42	4,65	4,65	4,47

Так как полученные значения константы диссоциации незначительно различаются, можно сделать вывод о том, что закон разбавления Оствальда соблюдается для водных растворов угольной кислоты. Найдем среднюю величину К_д:

моль/л

Концентрацию, при которой степень диссоциации угольной кислоты составляет 0,05, выразим из уравнения (3.2):

моль/л

Концентрация ионов водорода в этом растворе будет равна:

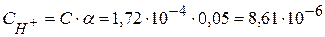моль/л

Так как концентрация ионов в растворе слабого электролита крайне мала, коэффициенты активности практически равны единице и активность не отличается от концентрации, тогда

.

Задача 2.

На основании данных об удельном сопротивлении водных растворов сильного электролита NaCl найдите его молярную электрическую проводимость при бесконечном разбавлении. Сравните полученное значение со справочными данными.

С, моль/л	0,1	0,05	0,03	0,01	0,005	0,003	0,001
r, Ом×м	1,05	1,88	2,99	8,33	16,27	26,62	78,50

Решение. Аналогично решению предыдущей задачи рассчитываем величины удельной и молярной электрической проводимости растворов хлорида натрия. Результаты сводим в таблицу:

С, моль/л	0,1	0,05	0,03	0,01	0,005	0,003	0,001
С^1/2	0,316	0,224	0,173	0,100	0,071	0,054	0,032
c, См/м	0,952	0,532	0,334	0,120	0,061	0,038	0,013
l, См×м^2/кмоль	9,52	10,64	11,15	12,00	12,29	12,52	12,74

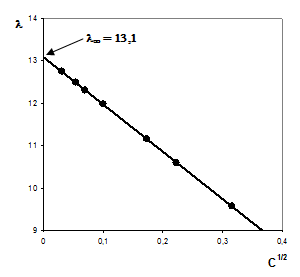
Для нахождения предельной молярной электрической проводимости используем уравнение Кольрауша (3.21). Решаем уравнение графическим методом, построив график зависимости l от С^1/2 и экстраполируя полученную прямолинейную зависимость на ось ординат (рис. 14):

По справочным данным, предельные подвижности катиона и аниона рассматриваемого электролита составляют:

l_¥ (Na⁺) = 5,2 См×м²/кмоль

l_¥ (Cl^-) = 7,9 См×м²/кмоль

Найдем величину l_¥ хлорида натрия в соответствии с законом независимого движения ионов Кольрауша (3.18):

l_¥ = 5,2 + 7,9 = 13,1 См×м²/кмоль

Полученная величина точно совпадает с определенной нами на основе экспериментальных данных.

Задача 3. Найдите рН раствора азотной кислоты с концентрацией 0,2 моль/л с учетом влияния ионной силы раствора.

Решение. Согласно схеме диссоциации азотной кислоты

HNO₃ → H⁺ + NO₃^-

концентрации ионов водорода и нитрат-ионов равны исходной концентрации HNO₃. Найдем ионную силу раствора по уравнению (3.9):

моль/л

Подставив полученное значение в выражение первого приближения Дебая (3.10), получим средний ионный коэффициент активности азотной кислоты в растворе:

;

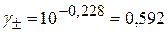
Найдем активность ионов водорода как произведение их концентрации на коэффициент активности кислоты:

моль/л

Тогда

Задача 4. Для окислительно-восстановительного элемента Pt │ Ce⁴⁺, Ce³⁺ ║ NbO³⁺, Nb³⁺ │ Pt по стандартным электродным потенциалам полуэлементов напишите уравнение и вычислите константы равновесия реакции окисления-восстановления. Вычислите ЭДС элемента при 298 К если активности Ce⁴⁺, Ce³⁺, NbO³⁺ и Nb³⁺ равны соответственно 0,02; 0,05; 0,03 и 0,01 моль/л. Укажите, можно ли практически изменить направление реакции за счет изменения концентраций компонентов. Считайте, что =1, = 0,2 моль/л.

Решение. По справочным данным, стандартные окислительно-восстановительные потенциалы j⁰ для систем Ce⁴⁺/ Ce³⁺ и NbO³⁺/ Nb³⁺ равны соответственно 1,77 и -0,34 В. Так как полуэлемент, содержащий систему церий (IV) – церий (III) обладает большим потенциалом, т.е. является положительным электродом – катодом, а электрод, погруженный в раствор ниобиевой окислительно-восстановительной системы служит отрицательным электродом – анодом. В связи с этим, схема гальванического элемента должна быть записана в виде

(-) Pt │ NbO³⁺, Nb³⁺ ║ Ce⁴⁺, Ce³⁺ │ Pt (+)

Так как на аноде происходит процесс окисления, а на катоде – восстановления, электродные реакции можно записать следующим образом:

A: Nb³⁺ + H₂O – 2e^- → NbO³⁺ + 2H⁺ (окисление) │x1

K: Ce⁴⁺ + e^- → Ce³⁺ (восстановление) │x2

Суммируя электродные реакции и учитывая, что для соблюдения баланса электронов вторую реакцию необходимо умножить на коэффициент 2, получим уравнение реакции, протекающей в гальваническом элементе:

2 Ce⁴⁺ + Nb³⁺ + H₂O → 2 Ce³⁺ + NbO³⁺ + 2H⁺

На основе уравнений электродных реакций и данных об активностях реагентов находим электродные потенциалы в соответствии с уравнением (3.27).

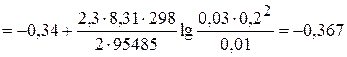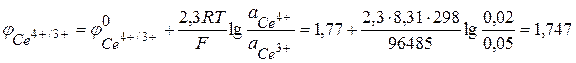В

В

ЭДС гальванического элемента рассчитаем по уравнению (3.52) как разность потенциалов катода и анода:

В

Аналогично стандартную ЭДС найдем как разность стандартных электродных потенциалов:

В

По уравнению (3.58) определяем константу равновесия реакции, протекающей в гальваническом элементе. При этом учитываем, что общее число электронов n, участвующих в реакции, равно 2.

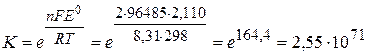
Так как константа равновесия очень велика (K>>1), равновесие практически полностью смещено в сторону продуктов реакции и изменить ее направление за счет изменения концентраций реагентов невозможно.

Основные понятия

Скоростью химической реакции называют изменение количества молей вещества в единицу времени в единице объема или изменение концентрации реагента в единицу времени t. Истинная скорость реакции находится как дифференциальная величина:

. (3.63)

Знак «+» в уравнении (3.63) используется в том случае, если берется концентрация продукта реакции, знак «-» ставят для исходных веществ, так как их концентрации убывают, т.е. dC< 0. В некоторых случаях используют также среднюю скорость реакции на конечном отрезке времени Dt. По аналогии с истинной скоростью, она находится в соответствии с уравнением

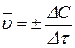. (3.64)

Скорость реакции тесно связана с механизмом ее протекания. Различают простые реакции, в которых исходные реагенты непосредственно превращаются в продукты, и сложные реакции, идущие в несколько стадий через образование ряда промежуточных продуктов (интермедиатов). Простая реакция (или отдельная стадия сложной реакции) может быть охарактеризована молекулярностью, т. е. числом молекул, одновременное взаимодействие которых друг с другом приводит к протеканию реакции. В зависимости от этого параметра реакции делят на:

1) мономолекулярные - элементарные реакции распада и изомеризации, в которых участвует только одна молекула, например разложение тетраоксида азота:

N₂O₄→2NO₂;

2) бимолекулярные, характеризующиеся столкновением двух частиц, например:

H + Cl₂ → HCl + Cl

Бимолекулярные реакции – самый распространенный тип простых реакций.

3) тримолекулярные реакции, протекающие за счет одновременного столкновения трех частиц, например:

2SO₂ + O₂ → 2SO₃

Молекулярность более 3 не встречается, поскольку одновременное столкновение четырех и большего числа молекул крайне маловероятно.

Скорость реакции зависит от концентрации реагентов. Эта зависимость описывается основным постулатом химической кинетики – законом действующих масс: скорость химической реакции в данный момент времени пропорциональна произведению текущих концентраций реагирующих веществ, возведенных в некоторые степени:

(3.65)

В данном уравнении k - константа скорости, для данной реакции зависящая только от температуры; n₁ … n_p - степени при концентрациях реагентов A₁…A_p, называемые частными порядками реакции по соответствующим веществам. Сумма всех частных порядков дает общий порядок реакции n:

n = n₁ + n₂ + … + n_p (3.66)

Если реакция является простой, то молекулярность и порядок совпадают, а частные порядки оказываются равными стехиометрическим коэффициентам в уравнении реакции. Так, для простой реакции образования нитрозилхлорида

2NO + Cl₂ → 2NOCl

закон действующих масс запишется в виде:

Так как порядок связан с молекулярностью, величина n не может быть больше 3, при этом простые реакции характеризуются первым, вторым или третьим порядком, а сложные могут также иметь нулевой и дробный порядок.

Кинетика простых реакций различного порядка

1. Реакции 1-го порядка. Для реакции A→B скорость прямо пропорциональна концентрации вещества А, обозначив которую как С запишем уравнение (3.65) следующим образом:

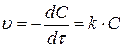(3.67)

Для нахождения зависимости концентрации от времени (кинетической кривой реакции) уравнение (3.67) интегрируют, принимая во внимание, что в начальный момент времени (t = 0) концентрация вещества А равна начальной C₀:

;

Решением интеграла является выражение или

(3.68)

Из уравнения (3.68) следует, что размерность константы скорости первого порядка равна [с^-1]. Допускается выражение времени и в других принятых единицах, тогда величина k может измеряться в [мин^-1], [ч^-1] и т. д. Кинетическая кривая реакции первого порядка имеет экспоненциальный характер и представлена на рис. 15 вместе с кривыми для реакций второго и третьего порядков.

Интегральное выражение кинетической кривой (3.68) можно представить также на основе данных не о концентрациях, а об убыли количества вещества. Если в начальный момент времени в системе находится a молей вещества A и к моменту времени t израсходуется x молей, то при объеме системы V концентрации могут быть представлены в виде

и ,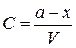

тогда

(3.69)

2. Реакции 2-го порядка. Такие реакции можно представить схемой

A + B → C

Согласно закону действующих масс, скорость можно найти по уравнению:

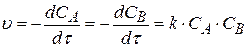(3.70)

Пусть начальные концентрации реагентов равны, т. е. C_A = C_B = C, тогда:

(3.71)

Интегрируя уравнение (3.71), получим

, или

(3.72)

Из уравнения (3.72) следует, что размерность константы скорости второго порядка составляет [c^-1×л×моль^-1]. Записывая уравнение (3.72) через убыль вещества, получим

(3.73)

Если объем системы в ходе реакции практически не меняется, то его вносят в константу:

(3.74)

В том случае, когда начальные концентрации реагентов неравны, представление концентраций через убыль количества вещества позволяет проинтегрировать уравнение (3.70):

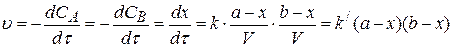(3.75)

где b – начальное количество вещества B.

(3.76)

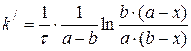(3.77)

3. Реакции 3-го порядка. В простейшем случае могут быть представлены схемой

A + B + C → D

В соответствии с уравнением (3.65), скорость реакции найдем как

(3.78)

В случае равенства концентраций по аналогии с (3.71) запишем:

(3.79)

Интегририрование уравнения (3.79) приводит к

, или

(3.80)

Из данного уравнения следует, что размерность константы скорости третьего порядка составляет [c^-1×л²×моль^-2]. Записывая уравнение (3.80) через убыль вещества, получим

(3.81)

Если объем системы в ходе реакции практически не меняется, то его вносят в константу:

(3.82)

Методы определения порядка реакции

Для экспериментального определения порядка реакции используются несколько основных методов. Принципиально их можно разделить на две группы – интегральные и дифференциальные. Первые основаны на использовании интегральных уравнений кинетических кривых, вторые подразумевают нахождение дифференциальной величины – скорости реакции.

К интегральным методам относят метод подстановки и метод полупревращения.

В методе подстановки на основе экспериментальных данных о зависимости концентрации от времени для каждого значения t рассчитывают константы скорости различных порядков по уравнениям (3.68), (3.72) и (3.80). Реакции приписывают тот порядок, для которого величина k является действительно константой, т. е. не меняется во времени (на практике наблюдается некоторый разброс значений около некоторого среднего из-за погрешностей измерения концентраций). Соответственно, монотонное увеличение или уменьшение величины константы скорости со временем означает неправильный выбор уравнения для ее расчета и, следовательно, неправильный выбор порядка реакции.

Разновидностью метода подстановки является графический метод, заключающийся в построении кинетической кривой реакции на графиках в различных координатах. Уравнения для констант скорости различных порядков (3.68), (3.72) и (3.80) могут быть записаны в следующих формах:

Для 1 порядка: (3.83)

Для 2 порядка: (3.84)

Для 3 порядка: (3.85)

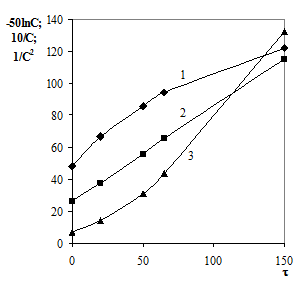
Отсюда следует, что в случае 1-го порядка наблюдается линейная зависимость в координатах lnC - t, в случае 2-го порядка - в координатах 1/С - t, реакции 3-го порядка характеризуются прямой в координатах 1/С² - t (рис. 16). Построив все три графика, выбирают тот порядок, для которого получается наиболее прямолинейная зависимость. При этом по тангенсу угла наклона прямой рассчитывается значение константы скорости.

Рис. 16. Линеаризация кинетических кривых для реакций первого (а), второго (б) и третьего (в) порядков.

Метод полупревращения (полураспада) основан на изучении зависимости времени полупревращения от начальной концентрации реагента. Временем полупревращения или полураспада t_1/2 называют время, за которое концентрация исходного вещества снижается в 2 раза по сравнению с начальной, другими словами, в данный момент времени соблюдается соотношение C = C₀/2. Подставляя это соотношение в уравнения (3.68), (3.72) и (3.80) и, соответственно, заменяя t на t_1/2 , получим:

Для 1 порядка: (3.86)

Для 2 порядка: (3.87)

Для 3 порядка: (3.88)

Таким образом, если реакция имеет первый порядок, время полупревращения не зависит от начальной концентрации. В случае второго порядка наблюдается обратная пропорциональность начальной концентрации. Для реакций третьего порядка t_1/2 обратно пропорциональна квадрату начальной концентрации.

Среди дифференциальных методов наибольшее распространение получил метод Вант-Гоффа. Если зависимость скорости реакции от концентрации описывается уравнением

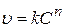, (3.89)

его можно линеаризовать логарифмированием:

(3.90)

Выражение (3.90) является уравнением прямой в координатах ln u - ln C. Тангенс угла наклона прямой соответствует порядку реакции, а отрезок, отсекаемый на оси ординат, равен логарифму константы скорости (рис. 17). Если имеется только два значения скорости при двух концентрациях, угловой коэффициент зависимости (3.90) удобнее определять расчетным путем:

(3.91)

Основным достоинством метода Вант-Гоффа является возможность определения не только целочисленных порядков, но также и дробных значений n. Существенный недостаток дифференциальных методов состоит в необходимости определения скорости реакции, т. е. дифференцирования кинетической кривой. Дифференцирование, особенно осуществляемое графически (определение тангенса угла наклона касательной к кинетической кривой в данной точке), ведет к неизбежным погрешностям, вследствие чего часто отказываются от использования в уравнении (3.91) истинной скорости, заменяя ее на среднюю:

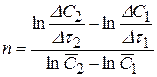(3.92)

где DС₁ и DС₂ – изменение концентрации, а и 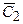- средние концентрации на отрезках времени Dt₁ и Dt₂ соответственно

Если в выражении закона действующих масс фигурируют концентрации нескольких реагентов, например

, (3.93)

то для определения общего порядка реакции сначала необходимо найти частные порядки по каждому реагенту, которые затем суммируются (см. выражение (3.66)). Для нахождения частных порядков, чтобы устранить мешающее влияние других реагентов, используют так называемый метод изолирования Оствальда, или метод понижения порядка реакции. Суть метода состоит в том, что зависимость скорости реакции от концентрации одного из реагентов изучают при постоянстве концентрации остальных реагентов. Неизменность концентрации в ходе реакции может быть достигнута использованием их в большом избытке. В таком случае, для определения n₁ в уравнении (3.93) проводим эксперимент при большом избытке реагента B и вносим постоянную величину в константу скорости:

(3.94)

Аналогично, создавая избыточную концентрацию реагента А для определения n₂, запишем

(3.95)

Уравнения (3.94) и (3.95) по форме не отличаются от уравнения (3.89), поэтому частные порядки в этом случае могут быть найдены любым из вышеперечисленных методов.

Влияние температуры на скорость реакции

Скорость химических реакций в подавляющем большинстве случаев резко увеличивается с ростом температуры. Согласно правилу Вант-Гоффа, при нагревании на 10°С скорость реакции, как правило, возрастает в 2…4 раза. Математическим выражением данного правила является уравнение:

(3.96)

где g - температурный коэффициент реакции

Для произвольного температурного интервала выражение (3.96) преобразуется к виду:

(3.97)

или

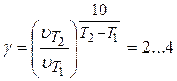(3.98)

Правило Вант-Гоффа лишь приближенно описывает зависимость скорости реакции от температуры и может быть использовано лишь для небольших диапазонов изменения температуры.

Для более точных расчетов следует использовать уравнения, полученные на основе представлений об активации молекул. Аррениус предположил, что в химическое взаимодействие могут вступать не все молекулы, а только небольшая их часть – молекулы, обладающие определенным запасом энергии и называемые активными. Для превращения обычных молекул в активные им нужно сообщить дополнительную энергию Е_а, называемую энергией активации, поэтому при нагревании их число быстро растет, что и ведет к увеличению скорости реакции.

Таким образом, простую реакцию первого порядка А → B, характеризующуюся константой скорости k, можно представить следующей схемой:

A⇄A* → B (3.99)

Константа скорости превращения активных молекул в продукты k₂ не зависит от температуры, поэтому влияние последней сводится только к сдвигу равновесия A⇄A*, т. е. к изменению константы равновесия K_c. Скорость реакции (3.99) определяется концентрацией активных молекул:

(3.100)

Так как связана с концентрацией вещества А константой равновесия

, (3.101)

то уравнение (3.100) приобретает вид:

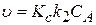(3.102)

В то же время, учитывая, что реакция А → B является простой, для нее в соответствии с законом действующих масс скорость определяется выражением:

(3.103)

Сравнив уравнения (3.102) и (3.103), получаем:

(3.104)

Так как k₂ не зависит от температуры, то

(3.105)

В соответствии с уравнением изохоры химической реакции, связывающим, константу равновесия с температурой

(3.106)

и, принимая во внимание, что тепловой эффект процесса активации DU можно отождествлять с энергией активации, получим уравнение Аррениуса в дифференциальной форме:

(3.107)

Интегрирование выражения (3.107) производится следующим образом:

(3.108)

(3.109)

Из уравнения (3.109) следует, что зависимость логарифма константы скорости реакции от обратной температуры линейна, а по угловому коэффициенту прямой можно определить энергию активации (рис. 18).

Уравнение (3.109) принято представлять в другой форме, избавляясь от логарифма в левой части:

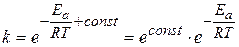(3.110)

Обозначив , получим классический вид уравнения Аррениуса:

(3.111)

Постоянная А в уравнении Аррениуса, не зависящая от температуры и определяемая только видом реакции, получила название предэкспоненциального множителя.

Если решение дифференциального уравнения (3.107) поводить в определенном интервале температур, тогда вместо выражения (3.108) запишем определенный интеграл:

(3.112)

решением которого является еще одна интегральная форма уравнения Аррениуса:

(3.113)

Уравнение (3.113) позволяет находить величину энергии активации, если известны значения констант скорости при двух температурах, а также рассчитывать константу скорости реакции при любой температуре при известной величине E_a и константе скорости при другой температуре.

По своей величине энергия активации сопоставима с теплотами химических реакций. Для большинства реакций в растворе она составляет 50-100 кДж/моль, в некоторых случаях достигая 200 и более кДж/моль. Так как E_a находится в степени уравнения (3.111) даже небольшое различие в энергиях активации приводит к огромной разнице в скоростях протекания реакций. Этим объясняется тот факт, что многие сходные реакции идут с совершенно различными скоростями.

Решение типовых задач

Задача 1. При термическом разложении ди- трет -бутилпероксида (ДТБП) образуются ацетон и этан. Измерение скорости этой реакции при 154,7°С дало следующие результаты:

t, мин
P ДТБП, Па	169,3	162,4	159,3	153,4	150,4	144,6	141,7	136,1	128,8	121,7

Определите порядок и константу скорости реакции.

Решение. Для определения порядка реакции воспользуемся методом подстановки. По уравнениям (3.68), (3.72) и (3.80) рассчитаем значения констант скорости соответственно первого (k_I), второго (k_II) и третьего (k_III) порядков. При этом давление газа, указанное в условии, будет играть роль его концентрации. Полученные результаты заносим в таблицу:

t, мин
kI ×10^2, мин^-1	-	2,08	2,03	1,97	1,97	1,97	1,98	1,98	1,95	1,94
kII ×10^4, Па^-1×мин^-1	-	1,25	1,24	1,22	1,24	1,26	1,28	1,31	1,33	1,36
kIII ×10^7, Па^-2×мин^-1	-	7,57	7,53	7,61	7,77	8,09	8,29	8,68	9,07	9,60

Из приведенных данных видно, что наиболее близкими являются значения константы скорости первого порядка. В случае второго и третьего порядков различие в величинах k для разных моментов времени заметно больше и, кроме того, наблюдается монотонное увеличение константы начиная с 3-5 минут. Поэтому можно сделать заключение, что реакция разложения ди- трет -бутилпероксида имеет первый порядок. Величину константы скорости находим усреднением найденных значений k_I:

k_Iср = 1,99×10^-2 мин^-1.

Задача 2. Изучалась кинетика изомеризации цианата аммония в мочевину:

NH₄CNO → (NH₂)₂CO

Цианат аммония массой 22,9 г растворили в воде и объем раствора довели до 1,00 л. При измерении содержания мочевины в растворе получены следующие данные:

t, мин		20,0	50,0	65,0
m (NH2)2CO, г		7,0	12,1	13,8	17,7

Определите порядок реакции. Рассчитайте константу скорости и массу цианата аммония через 300 мин после начала реакции.

Решение. Рассчитаем начальную концентрацию цианата аммония:

моль/л

Рассчитаем концентрации мочевины в различные моменты времени по уравнению:

Исходя из уравнения реакции, один моль цианата аммония превращается в 1 моль мочевины, поэтому текущая концентрация мочевины в любой момент времени равна убыли концентрации NH₄CNO. Концентрацию цианата аммония определяем по формуле:

Результаты расчетов сводим в таблицу:

t, мин		20,0	50,0	65,0
С (NH2)2CO, моль/л		0,117	0,202	0,230	0,295
С, моль/л	0,382	0,265	0,180	0,152	0,087

Порядок реакции находим графическим методом подстановки (рис. 19). Как видно из рис. 19, прямолинейная зависимость наблюдается только для координат 1/С - t. Константу скорости реакции второго порядка находим как тангенс угла наклона прямой (см. рис. 16):

л×моль^-1×мин^-1

Для нахождения массы цианата аммония через 300 мин после начала реакции воспользуемся уравнением для константы скорости реакции второго порядка (3.72), выражая из него текущую концентрацию C:

= 0,049 моль/л. Пересчитав концентрацию в массу реагента, получим:

г.

Задача 3. Кинетику реакции 2A → B, протекающей в жидкой фазе, изучали спектрофотометрическим методом и получили следующие данные:

t, мин						¥
СB, моль/л		0,089	0,153	0,200	0,230	0,312

Определите порядок реакции и константу скорости.

Решение: В условии задачи приведены концентрации продукта реакции, поэтому вначале следует пересчитать их в концентрации исходного вещества. Так как в начале процесса продукт отсутствует, то его текущая концентрация пропорциональна убыли вещества А. С учетом стехиометрических коэффициентов в уравнении реакции (из двух молей А получается один моль В) запишем:

откуда

(3.114)

Чтобы найти начальную концентрацию вещества А, воспользуемся данными для конца реакции (t = ¥), когда исходное вещество отсутствует в системе (C_A¥ = 0). В этом случае из уравнения (3.114) следует:

С_А0 = 2С_В¥ = 2×0,312 = 0,624 моль/л

Результаты расчетов по уравнению (3.114) сводим в таблицу:

t, мин						¥
СА, моль/л	0,624	0,446	0,318	0,224	0,164

Для определения порядка реакции воспользуемся методом подстановки. По уравнениям (3.68), (3.72) и (3.80) рассчитаем значения констант скорости соответственно первого (k_I), второго (k_II) и третьего (k_III) порядков. Полученные результаты заносим в таблицу:

t, мин						¥
kI, мин^-1	-	0,0336	0,0337	0,0342	0,0334	-
kII, л×моль^-1×мин^-1	-	0,0640	0,0771	0,0954	0,112	-
kIII, л^2×моль^-2×мин^-1	-	0,123	0,183	0,289	0,433	-

Из приведенных данных видно, что наиболее близкими являются значения константы скорости первого порядка, поэтому принимаем n = 1. Усредняя величины констант скорости первого порядка, получим k_ср = 0,0337 мин^-1.

Задача 4. Для реакции 2N₂O → 2N₂ + O₂ константа скорости при температуре 986 К равна 6,72 л×моль^-1×мин^-1, а при температуре 1165 К – 977,0 л×моль^-1×мин^-1. Найдите энергию активации этой реакции, температурный коэффициент и константу скорости при температуре 1053,0 К.

Решение. Температурный коэффициент реакции найдем по уравнению (3.98), используя в нем константы скорости реакции вместо скоростей:

Энергию активации реакции рассчитываем по интегральному уравнению Аррениуса (3.113), из которого следует, что:

Дж/моль = 265,54 кДж/моль

Обозначая температуру 1053,0 К в качестве T₃, найдем константу скорости при этой температуре k₃, воспользовавшись уравнением (3.113):

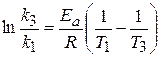
откуда

л×моль^-1×мин^-1.

Дата добавления: 2017-02-01