Таким образом, исходная система имеет единственное решение

,.

,,.

.

Таким образом, от исходной системы (8.1) мы перешли к равносильной системе (8.12), которая имеет треугольный вид (ступенчатый). Такое преобразование называют прямым ходом метода Гаусса.

Шаг. Затем преобразуем третье уравнение, исключив из него член, содержащий. Для этого обе части второго уравнения умножим на коэффициент при из третьего уравнения, взятый с противоположным знаком, т.е. на 3, получим

Для заметок

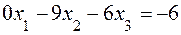. (8.9)

Обе части третьего уравнения умножим на коэффициент при 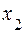из второго уравнения, т.е. на -3:

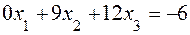. (8.10)

Сложим почленно уравнения (8.9) и (8.10):

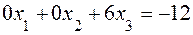. (8.11)

Заменим в системе (8.8) третье уравнение равносильным уравнением (8.11):

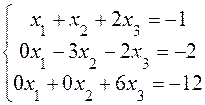. (8.12)

4 шаг (обратный ход). Из последнего уравнения системы (8.2) найдем :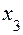

Используя второе уравнение и найденное значение 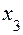, найдем :

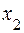Используя первое уравнение и найденное значение 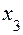и 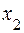, найдем :

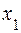Дата добавления: 2014-01-04