Ступенчатые матрицы и их ранг

Инвариантность ранга при элементарных преобразованиях

Теорема 11.2: Ранг матрицы при элементарных преобразованиях не меняется.

Для её доказательства рассмотрим следующие леммы:

Лемма №1: Пусть r(A)=k, тогда все миноры (k+1)-го порядка 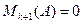, либо не существуют и (непосредственно следует из определения ранга).

Лемма №2: Если 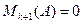для любого минора, то r(A)≤k.

Доказательство:

Разлагая минор (k+2)-го порядка матрицы А по какой-либо его строке, мы получим, что он представляется как сумма произведений элементов этой строки на их алгебраические дополнения, каждое из которых, с точностью до знака, совпадает с соответствующим минором (k+1)-го порядка матрицы А, и поэтому равны нулю. Поэтому всякий .

Разлагая далее любой минор (k+3)-го порядка по некоторой его строке, получим, что он равен сумме произведений элементов его строки на их алгебраические дополнения, которые являются (с точностью до знака) минорами (k+2)-го порядка матрицы А, и поэтому равен нулю. Итак, все .

По аналогии получим, что все (если они существуют), и лемма №2 доказана.

Лемма №3: Если r(A)=k, то определитель, состоящий из (k+1)-й строки матрицы А, равен нулю (его получают из минора (k+1)-го порядка с использованием замены строк местами). /она легко следует из леммы №1/

Лемма №4: Любое элементарное преобразование не увеличивает ранга матрицы.

Доказательство:

Пусть r(A)=k, а матрица В получается из матрицы А в результате какого-либо одного из элементарных преобразований строк первого типа (см. §9; лемма для элементарного преобразования строк второго типа будет следовать из её справедливости для элементарных преобразований первого типа, ибо всякое элементарное преобразование строк второго типа можно представить в виде последовательного действия одного или трёх преобразований первого типа).

Рассмотрим каждое из элементарных преобразований строк первого типа последовательно:

1) Замена строк местами: тогда любой состоит из (k+1)-й строки матрицы А (взятых, возможно, в другом порядке), и поэтому, по лемме №3, он равен нулю.

2) Умножение строки на число 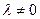(обозначение: – j-я строка матрицы А; 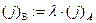– j-ю строку матрицы А умножаем на ).

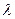Рассмотрим следующие случаи:

а) . Тогда в 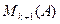ничего не изменилось, и поэтому, по лемме №1, .

б) 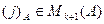. Тогда . (см. лемму №1)

3) Сложение строк (обозначение: – j-я строка матрицы В получается сложением (j)-й и (i)-й строк матрицы А). Рассмотрим следующие случаи:

а) , тогда в 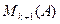ничего не изменилось, и поэтому, по лемме №1, .

б) . Последние 2 слагаемые являются минорами (k+1)-го порядка матрицы А, которые равны нулю по лемме №1 (во втором слагаемом может быть изменен порядок строк). Поэтому и в этом случае их сумма .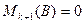

в) , ибо первое слагаемое в предпоследней сумме является минором (k+1)-го порядка матрицы А, который равен нулю по лемме №1 (r(A)= k), а второй определитель обращается в ноль, так как он имеет одинаковые строки (на месте его i-й и j-й строк находится одна и та же i-я строка матрицы А).

Мы показали, что для любого из элементарных преобразований любой 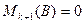, и поэтому, по лемме №2, r(B)≤k=r(A). (11.1)

Из леммы №4 легко следует

Лемма №5: Пусть из матрицы В получается матрица А конечным числом элементарных преобразований. Тогда r(B)≤r(A) (11.2)

Проведя обратные элементарные преобразования (от В к А), из леммы №5 получим, что r(А)≤r(В) (11.3)

Сопоставляя неравенства (11.2) и (11.3), имеем, что r(А)=r(В), и теорема 11.2 (об инвариантности ранга матрицы) доказана.

Дата добавления: 2014-01-04