
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторы, равенство векторов , коллиниарность и компланарность векторов, разность , умножение векторов. Свойства этих операций
|
|
|
|
Длина отрезка |АВ| - длина вектора 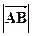
Под вектором обычно понимается величины, для задания которых необходимо знать не только их численное значение, но и направленное действие (Например, перемещение точки, скорость, ускорение, сила).
Величины для задания которых достаточно знать лишь их численное значение (например температура), называются скалярными величинами или скалярами. Обычно вектор обозначают как направленный отрезок.
 А В
А В
Определение: Система векторов 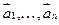 называется коллинеарной, а эти векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называется коллинеарной, а эти векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
 1) 2)
1) 2)
 | |||
 | |||
В первом случае векторы коллинеарны, во втором – сонаправлены.
Определение: Система компланарная, а векторы – компланарные, если векторы находятся в одной плоскости или на параллельных плоскостях.
(Два вектора всегда компланарны.)
Определение: 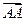 - нуль-вектор:
- нуль-вектор: 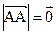
(Вектор, у которого конец и начало совпадают – нуль-вектор)
Этот вектор не имеет направления и коллинеарен любому вектору.
Свойства:
1. 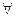


2. Если 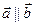 , то
, то 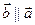
3. 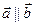 ,
, 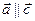 ,
,  ≠0 →
≠0 → 
Определение: Векторы равные, если:
1. они коллинеарные
2. равны по длине
3. направлены в одну сторону
Определение: Если векторы коллинеарны, равны по длине, направлены в разные стороны, то они противоположные.
Определение: Множество всех векторов, равных заданному, называется свободным векторам.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 575; Нарушение авторских прав?; Мы поможем в написании вашей работы!