
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ассоциативность
|
|
|
|
Свойства линейного пространства
1)  +
+  =
=  +
+  (очевидно, если сложить по правилу параллелограмма)
(очевидно, если сложить по правилу параллелограмма)
2) ( +
+  ) +
) + 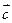 =
=  + (
+ ( +
+ 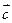 )
)
3)  +
+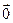 =
= 
4)  + (-
+ (-  ) =
) = 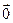
5) λ( +
+  ) = λ
) = λ  + λ
+ λ 
6) (λ + μ)  = λ
= λ  + μ
+ μ 
7) (λμ)  = λ(μ
= λ(μ  )
)
8) 1× =
= 
Докажем свойства 2) ÷ 8):
С

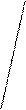
 +
+ 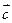 =
= 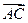
 +
+  =
= 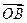
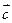
 + (
+ ( +
+ 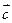 ) =
) = 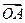 +
+ 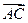 =
= 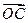 (14.1)
(14.1)


 (
( +
+  ) +
) + 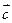 =
= 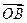 +
+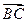 =
= 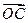 (14.2) В
(14.2) В
(14.1) = (14.2)

О  А
А
Рис 14.3
3) 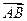 +
+ 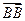 =
= 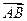
4) По определению:  –
–  =
=  + (-
+ (-  ).
).
 =
= 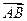 , тогда -
, тогда -  =
= 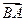 :
:  –
–  =
=  + (-
+ (-  ) =
) = 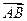 +
+ 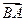 =
= 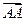 =
= 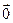
5) Пусть 
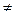 0,
0, 
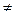 0, λ
0, λ 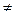 0 (иначе 5-е свойство становится тривиальным:
0 (иначе 5-е свойство становится тривиальным: 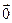 =
= 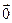 , или (при
, или (при  = 0); λ
= 0); λ  =
=  λ), предположим:
λ), предположим:  и
и  неколлинеарные.(случай
неколлинеарные.(случай  ||
||  будет доказан в §16 п.16.2)
будет доказан в §16 п.16.2)
Пусть точка О – начальная точка вектора  . (см. рисунок 14.4)
. (см. рисунок 14.4)
|
|


 =
= 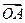
 =
= 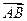 λ
λ  =
= 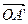 λ
λ  =
= 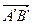
Также: 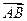 ||
|| 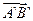 (т.к. λ
(т.к. λ  ||
||  ) и
) и 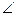 OAB =
OAB = 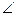 OA`B`.
OA`B`.
 Также:
Также: 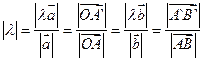 О А А’
О А А’
Рис 14.4
Поэтому ΔOA`B` ~ ΔOAB,  B`OA` =
B`OA` =  BOA, т.е точка B лежит на прямой OB’.
BOA, т.е точка B лежит на прямой OB’.
Но  ` =
` = 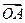 ` +
` + 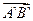 = λ
= λ  + λ
+ λ  (14.3);
(14.3);
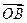 =
= 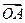 +
+ 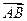 =
=  +
+  (14.4)
(14.4)
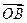 `||
`|| 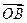 , т.к. ∆OAB ~ ∆OA’B’
, т.к. ∆OAB ~ ∆OA’B’ 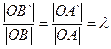 ,
, 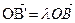 т.е. (14.5)
т.е. (14.5)
Подставляем (14.3) и (14.4) в (14.5) получаем λ  + λ
+ λ  = λ(
= λ( +
+  ).
).
6) Можно полагать, что λ 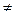 0, μ
0, μ 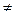 0,
0, 
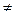 0, иначе свойство (6) становится тривиальным:
0, иначе свойство (6) становится тривиальным:
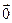 =
= 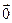 .
.
(или при μ = 0, λ  = λ
= λ  )по определению (см.14.2, правило 1)считаем, что λ
)по определению (см.14.2, правило 1)считаем, что λ  ║
║  , μ
, μ  ║
║  → (λa + μ
→ (λa + μ  ) ║
) ║  (14.7)
(14.7)
и (λ + μ)  ||
||
 (14.8).
(14.8).
Из (14.7) и (14.8) следует, что (λ+ μ)  || λ
|| λ  + μ
+ μ  .
.
Далее надо рассматривать следующие случаи:
а) λ > 0, μ > 0
б) λ > 0, μ < 0, λ + μ > 0
в) λ > 0, μ < 0, λ + μ < 0
г) λ < 0, μ < 0
Рассмотрим, например, случай (б): т.к. λ + μ > 0, то (λ + μ)  ↑↑
↑↑  , λ
, λ  ↑↑
↑↑  , μ
, μ  ↑↓
↑↓  , т.е. μ
, т.е. μ  ↑↓λ
↑↓λ  .
.
Поэтому вектор 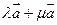 коллинеарен как
коллинеарен как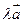 , так и
, так и  , и направлен в сторону более
, и направлен в сторону более
длинного вектора, т.е. 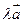 .
.
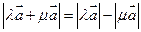 (14.10)
(14.10)
Из случая (б) имеем: 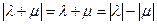 , т.е.
, т.е. 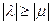
из (14.10) следует 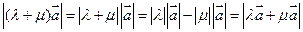 (14.11)
(14.11)
т.е. векторы 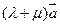 и
и 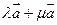 имеют одинаковую длину.
имеют одинаковую длину.
Заметим, что 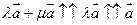 , ибо
, ибо 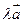 имеет большую длину, чем
имеет большую длину, чем 
Поэтому 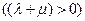
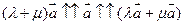 и случай б) доказан
и случай б) доказан
(Остальные случаи читателю предоставим рассмотреть самостоятельно.)
7) Заметим, что 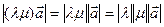 (14.12)
(14.12)
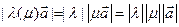 т.е. (см 14.12));
т.е. (см 14.12)); 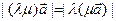 (14.13)
(14.13)
Покажем, что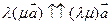 (14.14)
(14.14)
Для чего рассмотрим следующие случаи:
а) 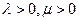 б)
б) 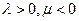 в)
в) 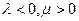 г)
г) 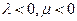
Рассмотрим, например, случай (в) (остальные случаи просим читателя рассмотреть самостоятельно):
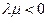 и потому
и потому 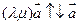 (14.15)
(14.15)
также 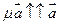 ,
, 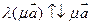 , т.е.
, т.е. 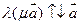 (14.16)
(14.16)
сопоставляя (14.15) и (14.16), получим (14.14).
8) 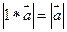 и
и 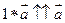 , т.е.
, т.е. 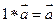
§15. Линейно – зависимые векторы и их свойства
Определение:
Система векторов 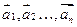 называется линейно-зависимой (л.з.), если
называется линейно-зависимой (л.з.), если 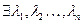 , не все из которых = 0 и
, не все из которых = 0 и 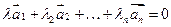 .
.
Определение:
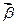 линейно выражается через
линейно выражается через 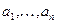 , если
, если 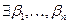 , что
, что 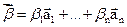
Свойства:
1) Если система содержит нуль-вектор, то она линейно зависима: 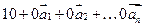 =
= 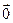 .
.
2) Если система имеет линейно зависимую подсистему, то она линейно зависима.
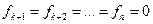
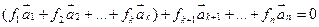 , т.к.
, т.к. 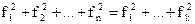
3) Система векторов линейно зависима, тогда и только тогда, когда хотя бы один вектор системы линейно выражается через остальные векторы.
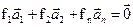 , если
, если 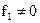 , то
, то 
Если же 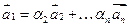 , то
, то 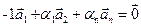 и система
и система 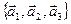 линейно зависима.
линейно зависима.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 389; Нарушение авторских прав?; Мы поможем в написании вашей работы!