Импульс

Я лекция. Полная механическая энергия системы частиц

Приращение кинетической энергии, полной механической энергии системы взаимодействующих частиц, находящихся во внешнем поле. Закон сохранения энергии.

Импульс системы частиц. Закон сохранения импульса. Центр масс. Система центра масс. Лабораторная система отсчета.

Уравнению второго закона Ньютона

можно придать другой вид. Учтя, что масса m в классической механике есть величина постоянная, ее можно внести под знак производной и записать (22.1) следующим образом:

Векторную величину

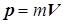
называют импульсом материальной точки¹). Воспользовавшись определением импульса, уравнение второго закона можно написать в виде

а сам закон сформулировать так: производная импульса материальной точки по времени равна результирующей всех сил, действующих на точку.

Уравнение (22.3) справедливо в более широких пределах, чем уравнение (22.1). Как устанавливает теория относительности, масса тела является функцией скорости: с увеличением скорости масса растет. Правда, зависимость массы от скорости такова²), что при скоростях значительно меньших скорости света, масса остается практически постоянной. Однако при больших скоростях масса начинает быстро расти, вследствие чего уравнение (22.1) становится неприменимым. В то же время уравнение (22.3) остается справедливым и при этих условиях. Таким образом, уравнение (22.3) сохраняет свое значение и в релятивистской механике (см. § 12).

Умножив (22.3) на dt, придем к соотношению:

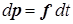
интегрирование которого дает приращение импульса за промежуток времени, протекший от момента t₁ до момента t₂:

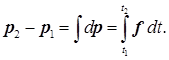
Отметим, что ранее вместо термина «импульс» пользовались термином «количество движения».

В специальной теории относительности в процессе выкладок сама собой в ряде случаев, например, при рассмотрении движения заряженной частицы в магнитном поле появляется аналитическая структура вида

Устаревшая интерпретация этого соотношения состоит в следующем: здесь m — масса тела в системе отсчета, относительно которой это тело движется со скоростью V, m ₀ — масса покоя, т. е. масса при V = 0, с — скорость света в вакууме. В действительности, здесь , то есть отношение энергии тела , движущегося со скоростью V к квадрату скорости света в вакууме и ничего больше. Масса тела есть релятивистский инвариант и от скорости движения тела не зависит.

Возвращаясь к формуле (22.5) в частном случае f = const, для приращения им­пуль­­­са за промежуток времени τ получаем: р ₂ — p ₁ = f ·t.

Заметим, что из выражения (22.3) следует, что, выяснив, как импульс изменяется со временем, можно установить силу, действующую на тело.

Дата добавления: 2014-01-04