
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функція, задана параметрично
|
|
|
|
Досі ми розглядали функції, задані рівнянням вигляду 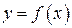 . В цьому випадку кажуть, що функція задана явним чином або є явною. Але функцію може визначати і рівняння вигляду
. В цьому випадку кажуть, що функція задана явним чином або є явною. Але функцію може визначати і рівняння вигляду
 , (4.1)
, (4.1)
не розв’язане відносно залежної змінної у. Тут заданому значенню 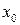 незалежної змінної ставиться у відповідність значення
незалежної змінної ставиться у відповідність значення  , яке є коренем рівняння з одним невідомим
, яке є коренем рівняння з одним невідомим
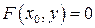 .
.
Цей корінь повинен бути єдиним для того, щоб можна було говорити про функцію, задану рівнянням (4.1), інакше даному значенню х відповідатимуть кілька значень у, що суперечить означенню функції. Про функцію, задану рівнянням вигляду (4.1) кажуть, що вона задана неявно або неявною.
Приклади.
1. Рівняння 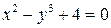 визначає у як неявну функцію від х, тому що кожному значенню х відповідає єдине значення у, в чому можна переконатися, розв’язавши рівняння відносно у і отримавши явний вираз для у:
визначає у як неявну функцію від х, тому що кожному значенню х відповідає єдине значення у, в чому можна переконатися, розв’язавши рівняння відносно у і отримавши явний вираз для у: 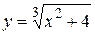 .
.
2. Тим часом рівняння 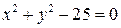 не визначає неявної функції, бо, наприклад, значенню
не визначає неявної функції, бо, наприклад, значенню  відповідають два значення
відповідають два значення  і
і  .
.
Зазначимо, що явну функцію 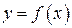 можна завжди записати як неявно задану рівнянням
можна завжди записати як неявно задану рівнянням  , але не навпаки, тому що не кожне рівняння вигляду (4.1) можна розв’язати відносно у. Слід мати на увазі, що терміни „явна функція” і „неявна функція” стосуються не природи функції, а способу її аналітичного завдання.
, але не навпаки, тому що не кожне рівняння вигляду (4.1) можна розв’язати відносно у. Слід мати на увазі, що терміни „явна функція” і „неявна функція” стосуються не природи функції, а способу її аналітичного завдання.
Важливою характеристикою функції є монотонність.
Означення. Розглянемо функцію 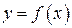 , визначену в інтервалі
, визначену в інтервалі 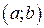 . Нехай
. Нехай  і
і 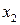 – довільні числа з цього інтервалу. Якщо з нерівності
– довільні числа з цього інтервалу. Якщо з нерівності  випливає, що
випливає, що
а)  , то функція
, то функція 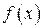 називається зростаючою;
називається зростаючою;
б) 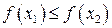 , то функція
, то функція 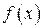 називається неспадною;
називається неспадною;
в) 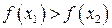 , то функція
, то функція 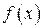 називається спадною;
називається спадною;
г) 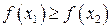 , то функція
, то функція 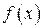 називається незростаючою;
називається незростаючою;
Зростаючі, незростаючі, спадні й неспадні функції в інтервалі 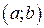 називаються монотонними в цьому інтервалі, а зростаючі і спадні – строго монотонними.
називаються монотонними в цьому інтервалі, а зростаючі і спадні – строго монотонними.
Нехай функція 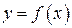 визначена на множині Х, а множиною її значень є
визначена на множині Х, а множиною її значень є  . Це означає, що кожному значенню
. Це означає, що кожному значенню 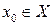 відповідає єдине значення
відповідає єдине значення 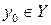 . Якщо при цьому різним значенням х відповідають різні значення у, то в свою чергу кожному значенню
. Якщо при цьому різним значенням х відповідають різні значення у, то в свою чергу кожному значенню 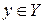 можна поставити у відповідність єдине значення
можна поставити у відповідність єдине значення  , таке, що
, таке, що 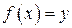 . Таким чином буде визначено функцію
. Таким чином буде визначено функцію 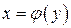 , яка визначена на множині
, яка визначена на множині  і має множину значень Х. Ця функція називається оберненою функцією до функції
і має множину значень Х. Ця функція називається оберненою функцією до функції 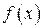 . Проілюструємо це схемою (рис. 4.1).
. Проілюструємо це схемою (рис. 4.1).

Рис. 4.1
Таким чином 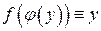 і
і 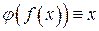 , тобто функції
, тобто функції 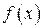 і
і  є взаємно оберненими. Зазначимо, що функцію, обернену до функції
є взаємно оберненими. Зазначимо, що функцію, обернену до функції 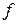 часто позначають як
часто позначають як  .
.
Приклади.
1. Якщо  , то
, то  .
.
Справді,  ;
;  .
.
2. Якщо 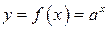 , то
, то  , бо
, бо
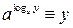 і
і  .
.
3. Якщо 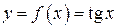 ,
, 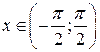 , то
, то 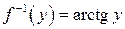 , бо
, бо
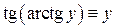 і
і 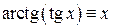 .
.
Теорема Якщо функція 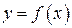 строго монотонна в інтервалі
строго монотонна в інтервалі 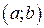 , то вона має обернену.
, то вона має обернену.
Дійсно, з означення строго монотонної функції випливає, що різним значенням аргументу ставляться у відповідність різні значення функції, а це внаслідок визначення оберненої функції і означає її наявність.
В розділі 3 йшла мова про те, що лінія на площині може бути задана параметричними рівняннями вигляду
 (3.5)
(3.5)
Нехай 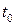 – яке-небудь число з проміжку
– яке-небудь число з проміжку  . Тоді
. Тоді  і
і  , тобто рівняння (3.5) ставлять у відповідність кожному числу
, тобто рівняння (3.5) ставлять у відповідність кожному числу 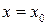 із області значень функції
із області значень функції  одне або кілька значень у із області значень функції
одне або кілька значень у із області значень функції  . Якщо при цьому кожному
. Якщо при цьому кожному 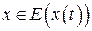 відповідає єдине значення
відповідає єдине значення 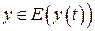 , то це означає, що рівняння (3.5) визначають функцію
, то це означає, що рівняння (3.5) визначають функцію 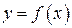 із областю визначення
із областю визначення 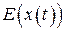 і областю значень
і областю значень 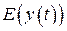 . Такий спосіб завдання функції
. Такий спосіб завдання функції 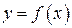 називається параметричним. Рівняння (3.5) визначають деяку криву на площині, отже і задана параметрично функція визначає на площині криву, а саме графік цієї функції, але не всяка параметрично задана лінія визначає функцію. Кожному значенню
називається параметричним. Рівняння (3.5) визначають деяку криву на площині, отже і задана параметрично функція визначає на площині криву, а саме графік цієї функції, але не всяка параметрично задана лінія визначає функцію. Кожному значенню 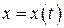 повинно відповідати єдине значення
повинно відповідати єдине значення  , а це можливо, якщо кожному значенню
, а це можливо, якщо кожному значенню 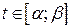 відповідає єдине значення х, тобто якщо функція
відповідає єдине значення х, тобто якщо функція 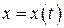 має обернену
має обернену  . Якщо ця обернена функція відома, то можна одержати явний вираз функції
. Якщо ця обернена функція відома, то можна одержати явний вираз функції 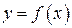 як складеної функції
як складеної функції
 .
.
Приклади.
1. Рівняння 
визначають функцію, оскільки змінна 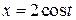 строго монотонна на відрізку
строго монотонна на відрізку 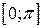 , отже має обернену, а саме
, отже має обернену, а саме 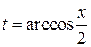 . Тоді явний вираз функції
. Тоді явний вираз функції
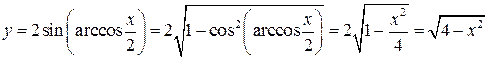 .
.
Таким чином задана функція має графіком півколо 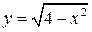 , розташоване у верхній півплощині, тому що при
, розташоване у верхній півплощині, тому що при 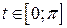 значення
значення 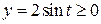 .
.
2. Рівняння 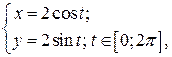
визначають на площині коло 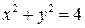 , але функцію не визначають. Справді, наприклад,
, але функцію не визначають. Справді, наприклад, 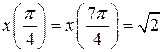 , тоді як
, тоді як 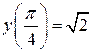 , а
, а 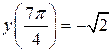 .
.
Зауважимо, що явне чи параметричне визначення функції характеризують не природу функції, а лише спосіб її аналітичного завдання.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 952; Нарушение авторских прав?; Мы поможем в написании вашей работы!