Властивості границь

1. Функція не може мати в даній точці дві різних границі.

Доведення. Припустимо, що в точці функція має дві різних границі – числа a ₁ і a ₂. Тоді за ознакою границі для будь-якого додатного числа 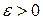існує таке додатне число (залежне від 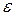), що для всіх значень x із проколеного 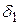–околу точки x ₀ виконується нерівність | f (x) – a ₁| < 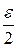і існує таке додатне число 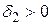, що для всіх значень x із проколеного 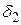–околу точки x ₀ виконується нерівність | f (x) – a ₂| < 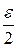. Нехай 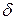- менше з чисел 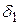та 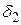. Тоді для всіх значень x із проколеного 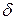–околу точки x ₀ виконується нерівність

| a ₂ – a ₁| = | a ₂ – f (x) + f (x) – a ₁| £ | a ₂ – f (x) | + | f (x) – a ₁| < + =.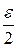

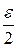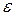Таким чином, вираз | a ₂ – a ₁| менше будь-якого додатного числа 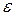. Таке може бути тільки тоді, коли | a ₂ – a ₁| = 0, тобто a ₂ = a ₁.

2. Границя сталої функції в будь-якій точці дорівнює цій сталій.

Доведення. Нехай f (x) = С = const. Тоді для будь-якого 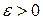і для будь-якого 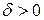| f (x) – С | = | С – С | = 0 < e, тобто f (x) = C.

3. Якщо функція f (x) має в точці x ₀ границю a, то ця функція обмежена в деякому околі 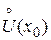точки x ₀.

Доведення. Згідно з означенням границі функції для будь-якого додатного числа 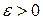існує таке додатне число 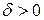, що для всіх значень x із проколеного 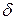–околу точки x ₀ виконується нерівність | f (x) – a | < e. З цієї нерівності маємо: – e < f (x) – a < e, тобто a – e < f (x) < a + e. Це і означає, що функція f (x) обмежена в 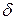–околі точки x ₀.

4. Якщо існують границі f (x) і g (x), то вірні наступні твердження:

а) (f (x) + g (x)) = f (x) + g (x);

б) (f (x) × g (x)) = f (x) × g (x);

в) якщо g (x) ¹ 0, то ;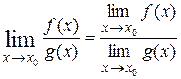

г) якщо и (x) = а, 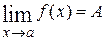, то границя складеної функції .

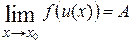Доведення. Доведемо твердження а), інші доводяться аналогічно.

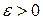Нехай f (x) = a ₁, g (x) = a ₂. Тоді для будь-якого додатного числа існує таке додатне число (залежне від 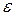), що для всіх значень x із проколеного 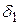–околу точки x ₀ виконується нерівність | f (x) – a ₁| < 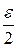і існує таке додатне число 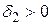, що для всіх значень x із проколеного 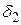–околу точки x ₀ виконується нерівність | g (x) – a ₂| < 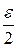. Нехай 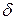- менше з чисел 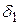та 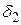. Тоді для всіх значень x із проколеного 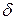–околу точки x ₀ виконується нерівність

|(f (x) + g (x)) – (a ₁ + a ₂)| =

= | f (x) – a ₁ + g (x) – a ₂| £ | f (x) – a ₁| + | g (x) – a ₂| < + =.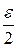

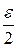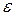Таким чином, (f (x) + g (x)) = a ₁ + a ₂.

Наслідки. а) Границя алгебраїчної суми скінченого числа функцій дорівнює сумі границь доданків, якщо ці границі існують.

б) Границя добутку скінченного числа функцій дорівнює добутку границь множників, якщо ці границі існують.

в) Сталий множник можна виносити за знак границі:

(С×f (x)) = С×f (x).

5. Якщо існує f (x) і в деякому проколеному околі 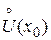має місце нерівність f (x) £ с (f (x) ³ с), то і f (x) £ с (f (x) ³ с).

6. Якщо існують f (x) і g (x), причому f (x) = g (x) = a, і в деякому проколеному околі точки мають місце нерівності f (x) £ h (x) £ g (x), то існує h (x) = a.

Зауваження. Всі властивості границь мають місце і для границі функції на нескінченності.

Приклад. Знайти границі

а) ;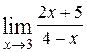

б) ;

в) .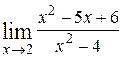

Розв'язання. а) Скористаємось властивостями границі 2, 4 та наслідками з властивості 4:

= = =.

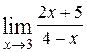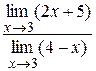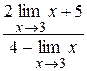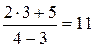б) При розв’язанні цього прикладу ми не можемо скористатись властивістю границь 4 в), тому що і чисельник, і знаменник дробу є нескінченно великими функціями, тобто не мають границі. В такому випадку говорять, що це невизначеність виду 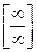. Перетворимо вираз під знаком границі:

.

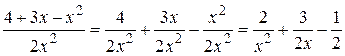Функції 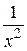та 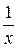є нескінченно малими при, тому що х ² та х є нескінченно великими (див. теорему про зв'язок між нескінченно малими і нескінченно великими функціями). Тепер можна скористатись властивостями границі 2, 4 та наслідками з властивості 4:

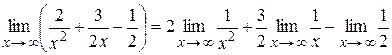= = = 2×0 +×0 - = -.

в) В цьому випадку ми не можемо скористатись властивістю границь 4 в), тому що знаменник дробу обертається в нуль у граничній точці. Чисельник також обертається в нуль в цій точці, тобто ми маємо невизначеність виду. Розкладемо чисельник і знаменник дробу на множники:

х ² – 4 = (х – 2)(х + 2) - за формулою скороченого множення.

Щоб розкласти на множники чисельник, знайдемо його корені: х ² – 5 х + 6 = 0. За відомими формулами або за теоремою Вієта х ₁ = 2, х ₂ = 3. Тоді

х ² – 5 х + 6 = (х – 2)(х – 3).

Таким чином, 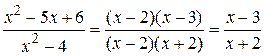. Знаменник останнього дробу вже не обертається в нуль у граничній точці, і можна скористатись властивостями границь:

.

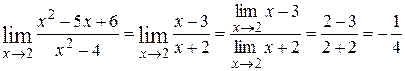Дата добавления: 2014-01-04