Вимушені коливання. Для того, щоб в реальній коливній системі забезпечити незгасаючі коливання, необхідно постійно до неї підводити енергію ззовні

Для того, щоб в реальній коливній системі забезпечити незгасаючі коливання, необхідно постійно до неї підводити енергію ззовні. І тому розглянемо коливання матеріальної точки, на яку, крім квазіпружної сили 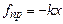і сили опору 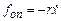, діє додаткова періодична змушувальна сила

,

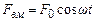де w –частота цієї сили.

Тоді за другим законом Ньютона маємо

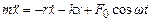. (5.37)

Перепишемо рівняння (5.37) у вигляді

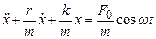
або

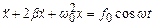, (5.38)

де .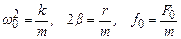

Розв’язок рівняння (5.38) будемо шукати як суму розв’язку однорідного рівняння (5.29) і часткового розв’язку неоднорідного рівняння: 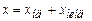. Для віддалених моментів часу 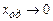. І тому

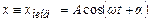. (5.39)

Отже, вимушені коливання здійснюються з частотою ω. Для знаходження амплітуди А і початкової фази α продиференціюємо двічі (5.39):

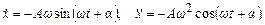(5.40)

Підставляючи (5.39) і (5.40) у (5.38), отримаємо:

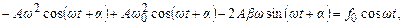
а розкриваючи тригонометричні функції від складного аргументу:

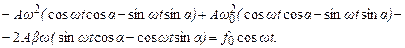(5.41)

Щоб рівняння (5.41) перетворилося в тотожність, потрібно, щоб суми коефіцієнтів при 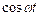в обох частинах рівності були рівні і суми коефіцієнтів при 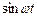в обох частинах були також рівні. Це означає, що

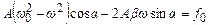, (5.42)

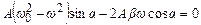. (5.43)

Із рівняння (5.43) отримаємо вираз для початкової фази вимушених коливань:

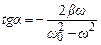. (5.44)

Підносячи до квадрату рівняння (5.42) і (5.43) та складаючи отримані вирази, одержимо:

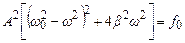
Звідси амплітуда вимушених коливань

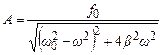. (5.45)

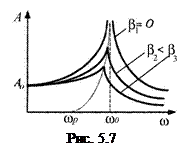
Проаналізуємо аналітично і графічно (рис. 5.7) залежність цієї величини від частоти w при різних значеннях коефіцієнту згасання β. Зокрема:

1) при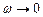

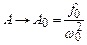
2) при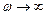

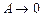
3) при ;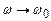

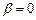
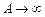
Досягнення максимального значення амплітуди вимушених коливань, коли частота ω наближається до власної частоти ω ₀, називається резонансом.

Для знаходження резонансної частоти при 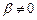знайдемо мінімум підкореневого виразу рівняння (5.45). Для цього прирівняємо до нуля похідну від цього виразу по w:

.

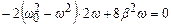Оскільки 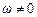, то знаменник (5.45) досягає мінімуму при

.

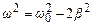Отже, резонансна частота

.

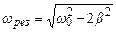Резонансна (максимальна) амплітуда досягає значення

.

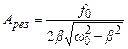Зрозуміло, що резонанс тим гостріший, чим менший коефіцієнт згасання. На практиці слід враховувати явище резонансу, оскільки в техніці він в одних випадках відіграє позитивну роль, а в інших – негативну.

Дата добавления: 2014-01-04