
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 1: Теория булевых функций и теория k-значных функций
|
|
|
|
Тема 0: Введение
Симферополь, 2004
ПО ДИСЦИПЛИНЕ Дискретная математика
КОНСПЕКТЫ ЛЕКЦИЙ
для студентов дневной (заочной) формы обучения
направления 0802 Прикладная математика,
специальностей 6.080200 Информатика,
6.080200 Прикладная информатика
| Составитель:доктор физико-математических наук, профессор Донской В.И. | |
| Рассмотрены и рекомендованы на заседании кафедры ……………………………. от «__» _____200_г. (протокол №_) |
Лекция 1. Предмет, мета та задачі дискретної математики
1) Непрерывность и дискретность [1,2,3,5]
2) Конструктивные объекты и задача синтеза. Ведение в теорию множеств и отношений [1,2,3,4,5]
Литература:
1. Яблонский С.В. Введение в дискретную математику. М.:Высш. шк., 2001. – 384 с.
2. Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. М.: Наука, 1977. – 386 с.
3. Гиндикин С. Г. Алгебра логики в задачах. М.: Наука, 1972.- 288 с.
4. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.
5. Донской В. И. Дискретная математика. – Симферополь: Сонат, 2000. –356 с.
Лекция 1. Предмет, мета та задачі дискретної математики
1) Основные понятия теории булевых функций [1,2,3,5]
Вектор 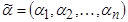 , координаты которого принимают значения из множества {0,1}, называется двоичным (булевым) вектором длины n.
, координаты которого принимают значения из множества {0,1}, называется двоичным (булевым) вектором длины n.
Множество всех булевых векторов длины n называется единичным n-мерным кубом и обозначается Bn. Весом или нормой вектора  называется число ||
называется число ||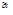 || =
|| =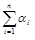 .
.
Множество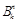 всех вершин куба, вес которых равен k, называется k -м слоем куба Bn. Число
всех вершин куба, вес которых равен k, называется k -м слоем куба Bn. Число 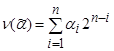 называется номером вектора
называется номером вектора 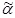 .
.
Число 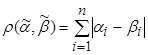 — называется расстоянием Хемминга.
— называется расстоянием Хемминга.
Наборы (векторы) 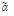 и
и 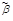 называются соседними, если
называются соседними, если 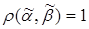 , и противоположными, если
, и противоположными, если  .
.
Говорят, что набор  предшествует набору
предшествует набору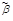 (обозначение:
(обозначение: 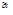
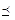
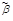 ), если для всех i =1 ,...,n ai
), если для всех i =1 ,...,n ai 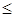 bi. Если при этом
bi. Если при этом 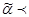
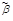 , то говорят, что
, то говорят, что  строго предшествует
строго предшествует 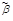 (обозначение
(обозначение 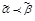 ). Если выполняется условие (
). Если выполняется условие (
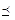
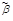 ) или (
) или (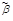
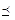
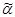 ), то
), то 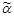 и
и 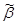 называют сравнимыми наборами, иначе — несравнимыми. Последовательность вершин куба Bn
называют сравнимыми наборами, иначе — несравнимыми. Последовательность вершин куба Bn 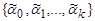 называется цепью, соединяющей
называется цепью, соединяющей 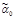 и
и 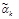 , если
, если 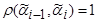 для i= 1 ,..,k, все вершины в последовательности различны. Число k называется длиной цепи. Цепь называется возрастающей, если
для i= 1 ,..,k, все вершины в последовательности различны. Число k называется длиной цепи. Цепь называется возрастающей, если 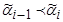 для i= 1 ,...k. Если
для i= 1 ,...k. Если 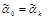 , то цепь называют циклом.
, то цепь называют циклом.
Множество 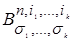 всех наборов (a 1 ,...,an) из
всех наборов (a 1 ,...,an) из 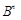 , у которых aij =
, у которых aij = .
.
(j= 1 ,...,k), называется гранью куба Bn. Множество номеров перeменных I= { i 1 ,...,ik } называется направлением грани, число k — рангом грани, (n-k) — размерностью грани. Интервалом куба Bn называется множество вида 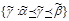 . Число
. Число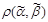 называется размерностью интервала.
называется размерностью интервала.
2) Реализация булевых функций формулами [1,2,3,5]
Функция f (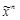 ), определенная на множестве Bn и принимающая значения из множества {0,1}, называется функцией алгебры логики или булевой функцией. Множество всех булевых функций обозначается P 2.
), определенная на множестве Bn и принимающая значения из множества {0,1}, называется функцией алгебры логики или булевой функцией. Множество всех булевых функций обозначается P 2.
Функциональные символы: & - конъюнкция, 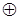 - сумма по модулю 2,
- сумма по модулю 2, 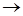 - импликация, V - дизъюнкция, ~ - эквивалентность, / - штрих Шеффера,
- импликация, V - дизъюнкция, ~ - эквивалентность, / - штрих Шеффера, 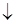 - стрелка Пирса называются логическими связками.
- стрелка Пирса называются логическими связками.
Элементарные булевы функции:
- одной переменной:
| X | 1 |
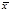
| 0 - тождественный ноль 1 - тождественная единица | ||
| x - тождественная функция | |||||
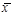 - инверсия (отрицание) - инверсия (отрицание)
|
- двух переменных:
| x | y | x & y | x V y | x 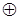 y y
| x~y | x 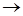 y y
| x/y | x 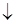 y y
|
Функция 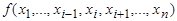 из P 2 зависит существенным образом от аргумента
из P 2 зависит существенным образом от аргумента 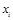 , если существуют такие значения
, если существуют такие значения 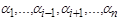 переменных
переменных 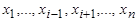 , что
, что 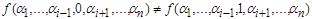 . В этом случае переменная
. В этом случае переменная 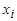 называется существенной. Если
называется существенной. Если 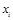 не является существенной переменной, то она называется фиктивной.
не является существенной переменной, то она называется фиктивной.
Формулой над множеством функциональных символов Ф называется вся-кое (и только такое) выражение вида: 1) 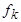 и
и 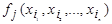 , где
, где 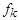 – нуль-местный, а
– нуль-местный, а 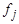 — n -местный функциональные символы и
— n -местный функциональные символы и 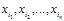 – символы переменных; 2)
– символы переменных; 2) 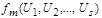 , где
, где 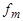 — s -местный функциональный символ и
— s -местный функциональный символ и 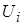 — либо формула над Ф, либо символ переменной.
— либо формула над Ф, либо символ переменной.
Формула называется тождественно истинной (тождественно ложной), если реализуемая ею функция равна 1 (соответственно 0).
3) Основные тождества [1,2,3,5]
x* y=y*x — коммутативность любой операции * из {&,V, 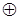 ,~,/,
,~,/,  }
}
(x * y) * z = x * (y * z) — ассоциативность любой операции * из {&,V, 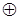 ,~}
,~}
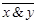 =
= 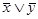 и
и 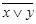 =
= 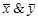 — тождества де Моргана
— тождества де Моргана
x V (x & y) = x и x & (x V y) = x — правила поглощения
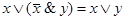 и
и
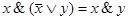 дистрибутивность:
дистрибутивность:
x & (y V z) = (x & y) V (x & z) — конъюнкции относительно дизъюнкции
x V (y & z) = (x V y) & (x V z) — дизъюнкции относительно конъюнкции
x & (y 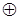 z) =(x & y)
z) =(x & y) 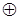 (x & z) — конъюнкции относительно сложения по mod 2
(x & z) — конъюнкции относительно сложения по mod 2
0 = x &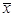 = x & 0 = x
= x & 0 = x 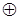 x, x =
x, x = 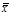 = x V x = x & x = x &1 = x V 0
= x V x = x & x = x &1 = x V 0
1 = x V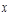 = x V1 = x~ x,
= x V1 = x~ x, 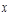 = x
= x 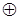 1, x~ y= (x
1, x~ y= (x 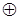 y)
y) 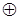 1
1
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 439; Нарушение авторских прав?; Мы поможем в написании вашей работы!