Лекция 2. Двойственность. Канонические формы булевых функций

1) Принцип двойственности [1,2,3,5]

Принцип двойственности: если формула 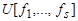реализует функцию 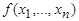, то формула 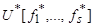реализует функцию .

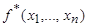2) Совершенная конъюнктивная нормальная форма [1,2,3,5]

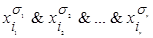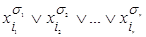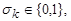
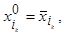
Формула (формула ), где 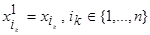для всех 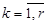— называется конъюнкцией (дизъюнкцией) над множеством переменных .

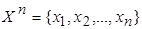Конъюнкция (дизъюнкция) называется элементарной (э.к., э.д.), если 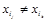при j 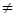k. Выражения вида 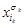будут называться буквами (литералами). Число символов (букв) в э.к. (э.д.) называется рангом э.к. (э.д.).

Формула вида K =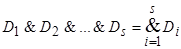, где 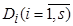– дизъюнкции, называется конъюнктивной нормальной формой (к.н.ф.). Число s называется длиной д.н.ф. (к.н.ф.).

3) Совершенная дизъюнктивная нормальная форма [1,2,3,5]

Формула вида D =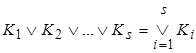, где 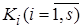– элементарные конъюнкции, называется дизъюнктивной нормальной формой (д.н.ф.).

Д.н.ф. называется совершенной, если она составлена из попарно различных элементарных конъюнкций ранга n.

Элементарная конъюнкция называется монотонной, если она не содержит отрицаний переменных.

4) Поліноми Жегалкіна [1,2,3,5]

Формула 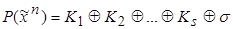, где 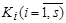– попарно различные монотонные элементарные конъюнкции, а 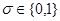, называется полиномом Жегалкина или полиномом по модулю 2. Наибольший из рангов э.к., входящих в полином, называется степенью этого полинома, число s называется длиной полинома.

Лекция 8. Введение в теорию k-значных функций

1) Основные понятия теории k-значной логики [1,2,3,5]

Пусть Е _k ={0,1,..., k -1}. Функция 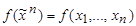называется функцией k -значной логики, если на всяком наборе 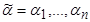значений переменных 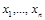, где , значение 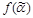также принадлежит множеству Е _k. Совокупность всех функций k -значной логики обозначается P _k.

,

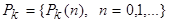
2) Реализация k-значных функций формулами. Операция суперпозиции [1,2,3,5]

Элементарные функции k -значной логики:

константы 0,1,..., k- 1;

отрицание Поста: 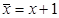(mod k); отрицание Лукашевича: ~ x = (k- 1)- x;

характеристические функции числа i: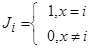

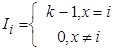
минимум x и y: min(x,y); максимум x и y: max(x,y);

сумма по модулю k: x + y (mod k); произведение по модулю k: x y (mod k);

усеченная разность: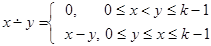

импликация: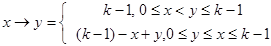

функция Вебба: v _k (x,y) = max(x,y)+1 (mod k);

разность по модулю k:

Функции min, max, +,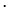 обладают свойствами коммутативности и ассоциативности. Кроме того, справедливы соотношения:

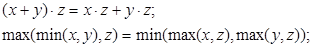
Вводятся по определению:

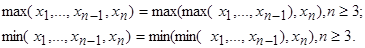
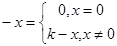
3) Тождества [1,2,3,5]

Любую функцию из Р _k можно представить в первой форме:

.

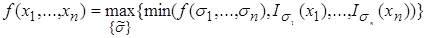Любую функцию из Р _k можно представить во второй форме:

,

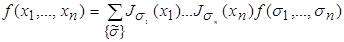где сложение и умножение берется по mod k.

Дата добавления: 2014-01-04