Тема 4. Введениие в теорию графов

Лекция 1. Определения и способы задания графов

1) Общие положения теории графов [1,2,3,4]

Пусть V — непустое множество, X — набор пар элементов из V. В наборе X могут встречаться пары, состоящие из одинаковых элементов, а также одинаковые пары. Множество V и набор X определяют граф с кратными ребрами G =(V,X). Элементы множества V называются вершинами графа, а элементы набора X — ребрами графа.

Если x =(u,v) — ребро графа, то вершины u и v называются концами ребра x. Если вершина v является концом ребра x, то говорят, что v и x — инцидентны.

Вершины u и v графа называются смежными, если существует ребро графа, соединяющее их. Два ребра называются смежными, если они имеют общую вершину. Степенью вершины v (обозначения deg (v)) называется число ребер графа, инцидентных вершине v.

Последовательность

, (*)

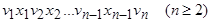в которой чередуются вершины и ребра и при этом для каждого i =1,…, n- 1 ребро имеет вид 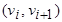, называется маршрутом, соединяющим вершины и . Число ребер в маршруте называется его длиной.

Маршрут, в котором все ребра разные, называется цепью. Маршрут, в котором все вершины разные, называется простой цепью. Маршрут (*) называется замкнутым, если =. Замкнутый маршрут, в котором все ребра различные, называется циклом. Цикл, в котором все вершины, кроме первой и последней, разные, называется простым циклом.

Граф называется связным, если для любых двух различных его вершин существует цепь (маршрут, простая цепь), соединяющая их. Расстоянием между вершинами связного графа называется длина кратчайшей цепи, соединяющей эти вершины.

2) Отношения и их свойства. Изоморфизм графов. [1,2,3,4]

Графы G =(V,X) и H =(U,Y) изоморфны, если существуют такие два взаимно однозначных соответствия , что для всякого ребра 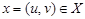справедливо соотношение.

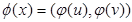3) Типы графов [1,2,3,4]

Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа. Компонентой связности графа G называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа графа G. Остовным называется граф, содержащий все вершины графа. Двудольным называется граф, множество вершин которого можно разбить на два непустых подмножества (доли) V ₁ и V ₂ таким образом, что никакие две вершины из одной и той же доли не являются смежными.

Деревом называется связный граф без циклов.

Теорема Кёнига: Граф является двудольным тогда и только тогда, когда в нем отсутствуют циклы нечетной длины.

4) Матрица смежности [1,2,3,4]

5) Матрица инцидентности [1,2,3,4]

Дата добавления: 2014-01-04