Тема 1.1 Основные понятия теории множеств

Множеством называется совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты. Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое".

Множество – это неопределяемое понятие, которое задается перечислением предметов, входящих (составляющих) в него, либо их свойствами.

Всякое множество состоит из элементов. Объекты, сущности или элементы, составляющие мно­жество, обозначаются строчными латинскими буквами: a, b, m, x, y …; множество часто обозначают прописными ла­тинскими буквами А, В, М, Х, У…. Знак Î обозначает вхож­дение или принадлежность; х Î Е читается: «элемент х принадлежит множеству Е», или короче: «х— элемент множества Е». Следует различать «общий элемент» х множества Е, т. е. произвольный элемент, характеризую­щийся единственным свойством «принадлежать множест­ву», и конкретные элементы а, b, c,..., каждый из ко­торых отличен от остальных. Если х не принадлежит Е, будем писать х Ï Е, что читается «х не является элемен­том множества Е» или «х не принадлежит множеству Е».

Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В, и записывают А Í В или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А Í А.

Множество называется конечным, если оно одержит конечное число элементов. Все остальные множества называются бесконечными.

Также необходимо выделить пустые множества. Множества, не содержащие элементы, называются пустыми. Принято считать, что пустое множество является подмножеством любого множества, Æ Í А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.

Существует два способа задания множества:

1) перечисление элементов (только для конечных множеств):

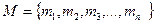
2) указание свойств:

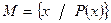- Множество М состоит из таких элементов х, обладающих свойством Р.

Пример:

1) - перечисление;

2)

Мощностью множества М называется число элементов в него входящих.

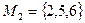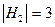, , где М₂ – множество, Н₂ – мощность множества;

Дата добавления: 2014-01-04