П Л А Н. 1. Конспект, підготовка до практичного заняття

Завдання додому

1. Конспект, підготовка до практичного заняття.

2. [2], с. 26-29

Питання для самоконтролю

1. Поняття матриці.

2. Застосування матриці в економіці.

3. Дії з матрицями, властивості.

Л Е К Ц І Я 3

Тема: Власні числа і власні вектори матриці. Квадратичні форми

Мета: сформувати поняття лінійного оператора; ознайомити з власними числами і власними векторами матриці, квадратичними формами

Література: [1, с. 16-18]; [6, с. 47-57].

1. Лінійні оператори

2. Власні числа і власні вектори матриці (лінійного оператора).

3. Квадратичні форми

1. Розглянемо 2 векторних простори Rⁿ та R^m.

Якщо заданий закон (правило), за яким кожному вектору 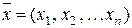простору Rⁿ ставиться у відповідність вектор 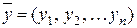простору R^m, то говорять, що заданий оператор (перетворення, відображення), який переводить вектор 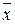з простору Rⁿ в простір R^m.

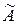- оператор

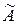(з тільдою (волною))

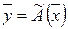- дія оператора над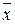

Вектор 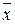називається прообразом вектору 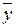, а вектор 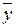– образом вектора .

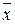Оператор називається лінійним, якщо він має такі властивості:

1) застосовується до суми векторів:

2) застосовується до добутку вектора на число:

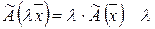- стале число.

Якщо простори Rⁿ і R^m збігаються, то оператор 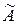відображає простір Rⁿ сам в себе.

Кожному оператору в деякому базисі ставиться у відповідність квадратична матриця, за допомогою якої можна виконати перетворення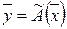

Введемо позначення у вигляді матриць:

,

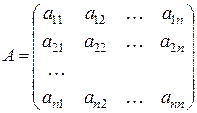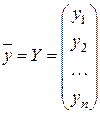
Запишемо перетворення за допомогою оператора у матричній формі:

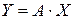
Приклад: Нехай в просторі R³ оператор 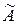, заданий матрицею 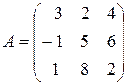і заданий в деякому базисі вектор 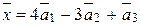, де ₁,₂,₃ –базисні вектори. Потрібно знайти образ 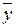в цьому ж базисі.

Запишемо в матричній формі:

Х=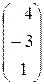

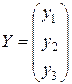
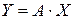
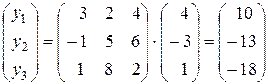
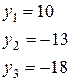
Тоді: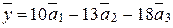

2. Нехай заданий лінійний оператор 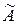у вигляді квадратної матриці

А=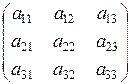

Ненульовий вектор 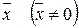називається власним вектором лінійного оператора 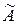, якщо знайдеться таке числ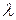о , що 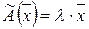. Число 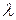називається власним числом або власним значенням оператора 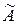, відповідним вектору .

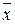З означення випливає, що власний вектор, під дією лінійного оператора 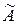переходе у вектор, колінеарний самому собі, тобто просто множиться на деяке число.

Поставимо задачу: для даного оператора знайти власні вектори і власні числа.

Запишемо в матричній формі рівність :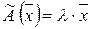

=

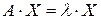
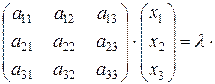
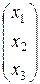
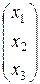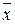
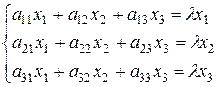
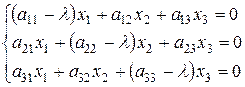
Це система лінійних однорідних рівнянь, яка завжди має нульовий розв’язок х₁=х₂=х₃=0. Але ж вектор 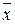=(х₁; х₂; х₃) ненульовий за умовою.

Нас цікавлять ненульові розв’язки системи, це значить, що головний визначник системи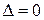

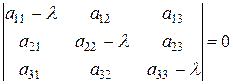
- характеристичне рівняння оператора 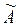(або матриці А).

Розв’язавши рівняння, знайдемо 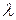, і, підставивши 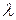в систему, знайдемо координати власного вектора.

Приклад: знайти власні числа і власні вектори оператора 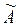, заданого матрицею А=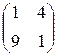

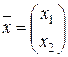
Запишемо систему:

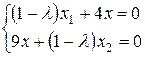
Складемо характеристичне рівняння:

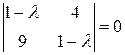
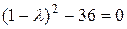
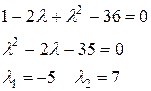за т. Вієта

Одержали два власних значення, значить для даного оператора існує два власних вектора.

1) Для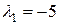

ё множина розв’язків

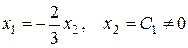
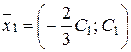
2) Для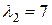

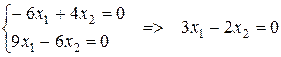множина розв’язків

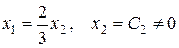
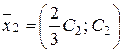
Зауваження: власні вектори і власні значення застосовуються для розв’язування економічних задач, зокрема в міжнародній торгівлі. За їх допомогою можна знайти національний прибуток кожної країни з врахуванням збалансованої торгівлі між країнами.

3. Квадратичною формою 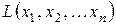від n змінних називається сума, кожний член якої є квадратом однієї із змінних або добутком двох різних змінних з деяким коефіцієнтом.

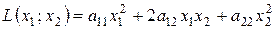
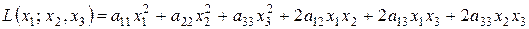
Кожній квадратичній формі ставиться у відповідність квадратна матриця.

Дано: 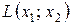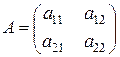, де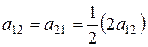

Приклад: Для даної квадратичної форми 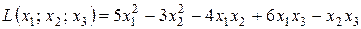- записати матрицю,

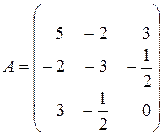
Коефіцієнти, симетричні відносно головної діагоналі, рівні між собою, така матриця називається симетричною.

Квадратична форма називається канонічною, якщо всі її коефіцієнт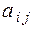и при 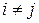дорівнюють 0.

Матриця в цьому випадку є діагональною.

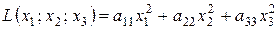
Квадратичну форму можна привести до канонічного виду за допомогою власних значень матриці квадратичної форми.

Приклад: квадратичну форму 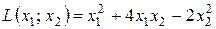привести до канонічного виду.

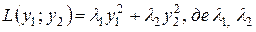- власні числа матриці квадратичної форми

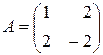
Характеристичне рівняння матриці:

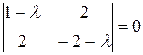
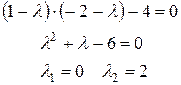
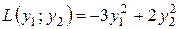
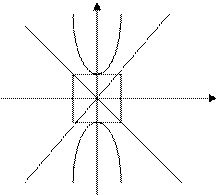
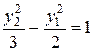гіпербола

Питання для самоконтролю

1. Лінійні оператори

2. Власні числа і власні вектори матриці (лінійного оператора).

3. Квадратичні форми

Л Е К Ц І Я 4

Тема: Розв’язування систем лінійних рівнянь

Мета: ознайомити з формулами Крамера розв’язування систем лінійних рівнянь; провести дослідження систем лінійних неоднорідних рівнянь, навчити дослідженню студентів

Література: [1, с. 20-24]; [6, с. 72-77].

Дата добавления: 2014-01-04