
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 1. Конспект, підготовка до практичного заняття. 1. Конспект, підготовка до практичного заняття
|
|
|
|
Завдання додому
1. Конспект, підготовка до практичного заняття.
2. [1] с. 84-93
Питання для самоконтролю
1. Рівняння площини в R3 .
2. Взаємне розташування площин.
3. Рівняння прямої в R3 .
4. Взаємне розташування прямих, прямої та площини.
5 Аналітична геометрія в економіці.
Л Е К Ц І Я 12
Тема: Функція однієї змінної. Границя функції
Мета: сформувати поняття функції, розглянути способи її задання; ознайомити границею змінної величини, нескінченно малими і нескінченно великими величинами, зв’язком між ними, границею функції, односторонніми границями.
Література: [1, с. 148-164]; [6, с. 205-218].
1. Означення функції, способи її задання.
2. Границя змінної величини. Нескінченно малі і нескінченно великі величини, їх зв’язок.
3. Границя функції. Односторонні границі.
1. Якщо кожному елементу х з деякої множини Х за певним правилом ставиться у відповідність єдиний елемент у з множини У, то говорять, що у є функція від х і пишуть у=f (x).*
*Це означення належить М.І.Лобачевскому і Л.Діріхле.
х – незалежна змінна (або аргумент).
у – залежна змінна (або значення функції).
Множина Х називається областю визначення функції, множина У – область значень.
Способи задання функції.
1 ) Аналітичний (за допомогою формули).
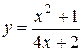
при 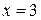
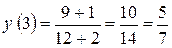
2 ) Графічний (за допомогою графіка).
 |
 у
у
у=х2
 0 х
0 х
3) Табличний
| х | -2 | -1 | |||
| у | -8 | -1 |
4) Словесний
Функція Діріхле: f (x)=1, якщо х – раціональне число; f (x)=0, якщо х – ірраціональне число.
2. Нехай в деякому процесі змінна величина х наближається до числа  , тоді говорять, що х прямує до
, тоді говорять, що х прямує до  і пишуть
і пишуть 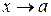 . Це значить, що починаючи з деякого значення, х приймає як завгодно близькі до числа
. Це значить, що починаючи з деякого значення, х приймає як завгодно близькі до числа  значення, але не рівні
значення, але не рівні  . Тоді говорять, що число
. Тоді говорять, що число  є границею змінної величини х, і пишуть
є границею змінної величини х, і пишуть
 =
=
Означення Число  називається границею змінної величини х, якщо для довільного числа
називається границею змінної величини х, якщо для довільного числа 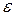 >0, починаючи з деякого значення, всі наступні значення х задовольняють нерівність
>0, починаючи з деякого значення, всі наступні значення х задовольняють нерівність 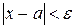 .
.
Тобто, починаючи з деякого значення, всі наступні значення х попадають
в 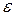 - окіл точки
- окіл точки  і в процесі зміни залишаються в цьому околі.
і в процесі зміни залишаються в цьому околі.
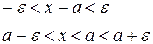
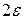
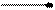
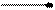
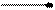
0 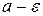

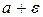 х
х
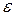
Нескінченно малі величини
Нехай змінна величина* х в деякому процесі нескінченно зменшуючись наближається до 0 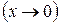 , тоді говорять, що х є нескінченно малою величиною.
, тоді говорять, що х є нескінченно малою величиною.
* Величина, границя якої дорівнює 0
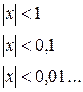
Означення. Змінна величина х називається нескінченно малою в процесі її зміни, якщо існує яке завгодно мале додатнє число 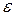 , таке, що починаючи з деякого значення, всі наступні значення х задовольняють нерівність
, таке, що починаючи з деякого значення, всі наступні значення х задовольняють нерівність 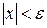 .
.
Тобто значення х попадає в 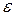 - окіл нуля.
- окіл нуля.
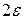
х х




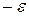 0
0 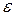
Властивості нескінченно малих величин
1) Сума (різниця) нескінченно малих величин є величина нескінченно мала.
2) Добуток нескінченно малих величин є величина нескінченно мала.
3) Частка від ділення нескінченно малої величини на функцію, яка має відмінну від нуля границю, є величина нескінченно мала.
4) Добуток обмеженої функції на нескінченно малу є величина нескінченно мала.
5) 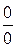 -невизначеність.
-невизначеність.
Нескінченно великі величини.
Означення. Змінна величина х називається нескінченно великою в деякому процесі, якщо для довільного як завгодно великого додатнього числа М її модуль більший від М: 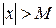 .
.
Говорять, що змінна х прямує до нескінченності і пишуть 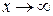
або lim 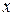 =
=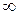
Нескінченно великі величини можуть бути і від’ємними, і додатніми.
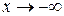 - нескінченно велика від’ємна величина
- нескінченно велика від’ємна величина
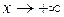 - нескінченно велика додатня величина
- нескінченно велика додатня величина
Властивості нескінченно великих величин
1) 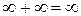
2) 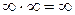
3) 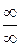 - невизначеність
- невизначеність
4) 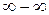 - невизначеність
- невизначеність
Зв’язок між нескінченно великими і нескінченно малими величинами
 Величина, обернена нескінченно великій, є нескінченно мала
Величина, обернена нескінченно великій, є нескінченно мала
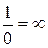 Величина, обернена нескінченно малій, є нескінченно велика
Величина, обернена нескінченно малій, є нескінченно велика
3. Нехай дана функція у=f (х). Число А називається границею функції f (х) при 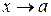 , якщо для всіх значень х, які як завгодно мало відрізняються від
, якщо для всіх значень х, які як завгодно мало відрізняються від  , відповідні значення у як завгодно мало відрізняються від А.
, відповідні значення у як завгодно мало відрізняються від А.

 f(x)=А
f(x)=А
 |


 у у= f(x) Означення
у у= f(x) Означення
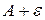 Число А називається границею
Число А називається границею
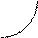

 А функції у= f(x) при
А функції у= f(x) при 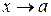 , якщо для
, якщо для
будь-якого наперед заданого скільки


 А-
А-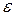 завгодно малого числа
завгодно малого числа 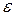 >0
>0
знайдеться таке число 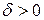 , що для
, що для

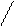 будь-якого х, відмінного від
будь-якого х, відмінного від  , при
, при
 0
0 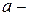
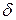

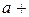
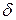 х виконанні нерівності
х виконанні нерівності 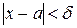 виконується нерівність
виконується нерівність 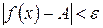 .
.
Якщо значення х попадає в 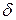 -окіл точки
-окіл точки  , то значення у попадає в
, то значення у попадає в
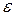 -окіл точки А.
-окіл точки А.
Правило обчислення границі
 f (x) = f (a), якщо f (a) існує.
f (x) = f (a), якщо f (a) існує.
Приклад: Знайти 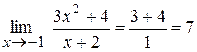
Властивості границь
1)  (f (x)+g (x)) =
(f (x)+g (x)) = f (x) +
f (x) + g (x)
g (x)
(якщо = f (x) і
f (x) і g (x) існують)
g (x) існують)
для всіх властивостей
2)  (f (x)
(f (x) 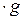 (x)) =
(x)) = f
f 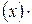
 g (x)
g (x)
3) 
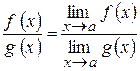 , якщо
, якщо  g (x)
g (x) 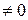
4)  c
c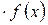 =
= 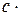
 f (x), де с – const
f (x), де с – const
5)  С=С, де С –const
С=С, де С –const
6) Для того, щоб число А було границею функції f (x) при 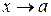 , необхідно і достатньо, щоб різниця f (x) – А була нескінченно малою величиною, тобто
, необхідно і достатньо, щоб різниця f (x) – А була нескінченно малою величиною, тобто
 f (x) =A <=>
f (x) =A <=> 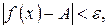
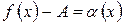
де 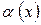 - нескінченно мала величина;
- нескінченно мала величина;
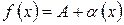
| Тобто функція мало відрізняється від своєї границі на |
нескінченно малий доданок: 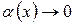 при
при 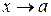
Односторонні границі
1) Лівостороння границя
Границя функції при 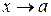 за умови, що х залишається меншим за
за умови, що х залишається меншим за  , називається лівосторонньою.
, називається лівосторонньою.


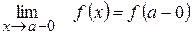
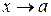 х
х
2) Правостороння границя
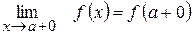

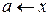 х
х
Приклад: 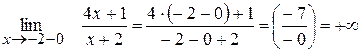
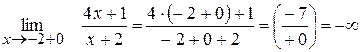
Одна з ознак існування границі (про границю проміжної функції)
Нехай функції 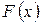 і Ф (х) при
і Ф (х) при 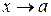 мають одну й ту ж границю:
мають одну й ту ж границю:
 F (x) =
F (x) =  Ф (х) =А. Нехай функція f (x) задовольняє нерівність
Ф (х) =А. Нехай функція f (x) задовольняє нерівність
F (x) f (x)
f (x) Ф (х). Перейдемо до lim при
Ф (х). Перейдемо до lim при 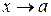 :
:
 F (x)
F (x)
 f (x)
f (x)
 Ф (х)
Ф (х)
А 
 f (x)
f (x)  A
A
 f (x) =A
f (x) =A
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 310; Нарушение авторских прав?; Мы поможем в написании вашей работы!