П Л А Н. 1. Конспект, підготовка до практичного заняття. 1. Конспект, підготовка до практичного заняття

Завдання додому

1. Конспект, підготовка до практичного заняття

2. Самостійна робота №5 “Графіки елементарних функцій” (2 год.)

[1] c. 138-142

3. Самостійна робота №6 “Границя послідовності” (2 год.)

[1] с. 149-153

4. Самостійна робота №7 “Порівняння нескінченно малих і нескінченно великих величин” (2 год.)

[2] с. 147-153

Питання для самоконтролю

1. Означення функції, способи її задання.

2. Границя змінної величини.

3. Нескінченно малі і нескінченно великі величини, їх зв’язок.

4. Границя функції. Односторонні границі.

Л Е К Ц І Я 13

Тема: Особливі границі

Мета: Ознайомити з першою та другою особливими границями, натуральними логарифмами, порівнянням нескінченно малих

Література: [1, с. 169-183]; [6, с. 212-216].

1. Перша особлива границя

2. Друга особлива границя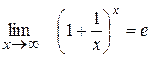

3. Натуральні логарифми.

4. Порівняння нескінченно малих.

1. Нехай дано круг радіуса R

У Радіанна міра АОВ,

(АОВ утворений радіусом

круга і віссю О_х).

А АС –дотична до кола в т.А

В С х

Порівнюючи площі 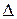АОВ, сектора круга АОВ і 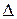АОС, дістанемо:

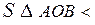
сект АОВ < S 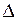АОС;

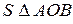=, S сект АОВ =,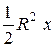

=;

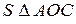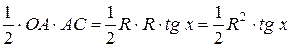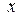
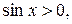так як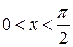

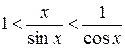
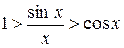
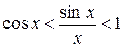
Перейдемо до границі при ;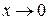

1;

1<, звідки

=1	- перша особлива границя

Для першої особливої границі невизначеність

Приклади: 1) 2)

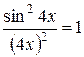
Для обчислення першої особливої границі застосовують формули тригонометрії (для перетворення виразів):

;

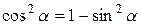
1

Приклад:

=

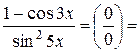
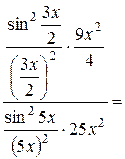
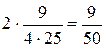
Наслідки першої особливої границі:

1)

2)

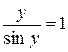
3)

3) Розглянемо множину логарифмичних кривих при умові, коли основа логарифма більша за 1: у=log _a x, a>1, x>0

у y=log _a x (а>1) Нехай до кожної кривої

проведена дотична в точці х=1

Серед цих кривих знайдеться

така, дотична до якої в т.х=1

нахилена до осі О_х під кутом 45⁰

0 1 x

Основою логарифма такої кривої є число е, значення його знаходиться в межах 2 < e < 3.

е=2,7182818284... е 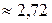- ірраціональне.

Число е називається числом Непера (на честь шотландського математика Дж. Непера – винахідника логарифмів) або числом Ейлера. Число е трансцендентне (тобто не є коренем алгебраїчного рівняння з цілими коефіцієнтами).

Логарифми за основою е називаються натуральними і позначаються ln x. Натуральні логарифми мають такі ж властивості, як і логарифми за любою основою:

1) ln 1 =0 7) lg =

2) ln e =1

3) ln ln ln

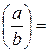4) lnln -ln

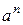5) ln =ln

6) ln =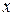

Число 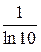називається модулем переходу від десяткового логарифма до натурального.

у y=ln x Побудуємо графік функції у=ln x

В АВ – пряма, яка перетинає

графік функції у=ln x в двох

А 45⁰ ln (1+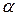) точках (січна).

0 С х

1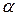

Нехай 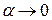, тоді т. В, переміщаючись по кривій, прямує до т. А (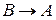). Січна АВ займе положення дотичної, проведеної в т.А в деякий момент. При цьому кут нахилу до осі О_х буде дорівнювати 45⁰ ().

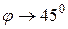З 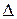АВС знайдемо : .

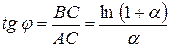Знайдемо

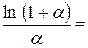
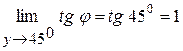
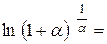ln =1

Зауваження: 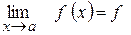(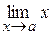) за властивістю границі, якщо функція неперервна, то можна поміняти місцями символи lim і f.

(границі) (функції)

Значить,

- друга особлива границя

Для другої особливої границі невизначеність 1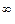

Другий запис другої особливої границі:

;

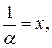
при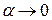

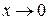
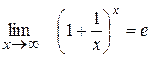
Приклад: 1)

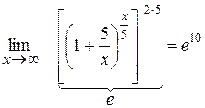
2)

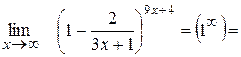
0

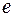
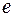= ==^-6 =

4. Дві нескінченно малі порівнюються між собою за допомогою дослідження їхнього відношення.

Нехай дано дві нескінченно малі:

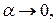
1) 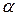і 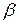називаються нескінченно малими одного порядку, якщо

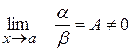, А є R.

2) 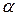називається нескінченно малою вищого порядку, ніж 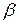, якщо .

3) 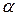називається нескінченно малою нижчого порядку, ніж 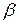, якщо .

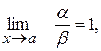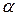4) Якщо то і 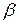- еквівалентні нескінченно малі .

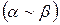Теорема про заміну відношення нескінченно малих відношенням еквівалентних величин: при знаходженні границі відношення нескінченно малих можна замінити їх еквівалентними величинами

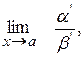де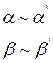

Еквівалентність деяких нескінченно малих (при ):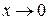

sin x ~ x, tg x ~ x, arcsin x ~ x,

arctg x ~ x, sin^kx ~x^k

Приклад:

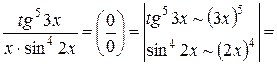
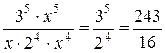
Дата добавления: 2014-01-04