КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Завдання додому
|
|
|
|
1. Конспект, підготовка до практичного заняття.
Питання для самоконтролю
1. Перша особлива границя 
2. Друга особлива границя 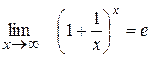
3. Натуральні логарифми.
4. Порівняння нескінченно малих.
Л Е К Ц І Я 14
Тема: Неперервність функції. Похідна. Диференціал функції у= f(x).
Мета: сформувати поняття неперервності функції; ознайомити з похідною, її метричним та економічним змістом, основними правилами диференціювання, таблицею похідних, похідною складної функції.
Література: [1, с. 191-222]; [6, с. 237-260].
П Л А Н
1. Неперервність функції у=f (x).
2. Похідна функції. Геометричний та економічний зміст.
3. Основні правила диференціювання.
4. Таблиця похідних.
5. Похідна складної функції.
6. Означення диференціала та його зміст.
7. Інваріантність форми диференціала.
8. Застосування диференціала в наближених обчисленнях.
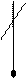 |  | ||
 1. Розглянемо у=f (x),
1. Розглянемо у=f (x),
 У х є [a; b]
У х є [a; b]



 dy х0 – початкова точка
dy х0 – початкова точка
 B у=f (x)
B у=f (x)
 Δу
Δу
 Дамо х0 приріст Δх, одержимо
Дамо х0 приріст Δх, одержимо
 A C
A C 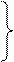


 f (x0+Δx) функцію f (x0+Δ)
f (x0+Δx) функцію f (x0+Δ)
Δx
f (x0)

 0 х0 х0+Δх х
0 х0 х0+Δх х
Різниця f (x0+Δ)-f (x0)=Δy називається приростом функції, відповідним приросту аргументу Δ х.
Означення. Функція у=f (х) називається неперервною в точці х0, якщо ця функція визначена в деякому околі точці х0 і якщо  Δу=0, тобто нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції.
Δу=0, тобто нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції.
Якщо границя приросту функції при  не дорівнює 0, то функція в точці х0 має розрив.
не дорівнює 0, то функція в точці х0 має розрив.
 у
у

х0 х
1. Означення. Функція у=f (х) називається неперервною на деякому проміжку
[ ], якщо вона неперервна в кожній точці цього проміжку.
], якщо вона неперервна в кожній точці цього проміжку.
2. Означення. Похідною функції у=f (х) називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.


Похідна позначається символами:
 .
.
Геометричний зміст похідної:
З Δ АВС: 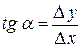
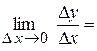
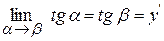
Похідна визначає тангенс кута нахилу дотичної до осі абсцис в початковій точці х0.
Економічний зміст похідної:
Продуктивність праці є похідною об’єму продукції за часом.
Похідна визначає швидкість зміни функції точці.
Операція знаходження похідної від функції y=f (x) називається диференціюванням цієї функції.
Нехай функція u=u (x) та v=v (x) – неперервні.
1) 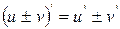
2) 
3) 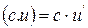 с – const
с – const
4) 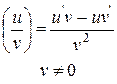
 с – const
с – const
 c – сonst
c – сonst
4. Таблиця похідних
| 1. | с’=0, с – const | |
| 2. | х’=1 | |
| 3. | 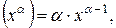 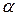 - довільне число - довільне число
| 3. 
|
| 4. | 
| 4. 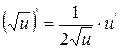
|
| 5. | 
| 5. 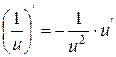
|
| 6. | 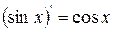
| 6. 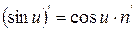
|
| 7. | 
| 7. 
|
| 8. | 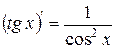
| 8. 
|
| 9. | 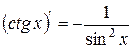
| 9. 
|
| 10. | 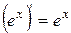
| 10. 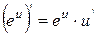
|
| 11. | 
| 11. 
|
| 12. | 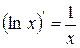
| 12. 
|
| 13. | 
| 13. 
|
| 14. | 
| 14. 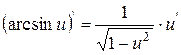
|
| 15. | 
| 15. 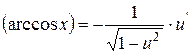
|
| 16. | 
| 16. 
|
| 17. | 
| 17. 
|
Приклад: 
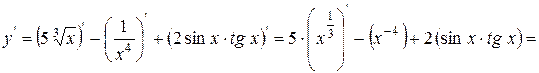
=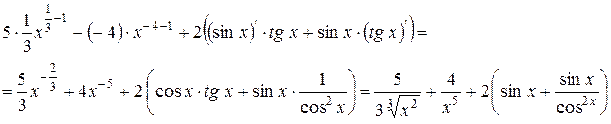
5. Нехай дана складна функція у=f (g (x)).
Щоб знайти похідну складної функції потрібно похідну від зовнішньої функції помножити на похідну від внутрішньої функції.
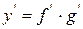 Приклади:
Приклади:
1) 
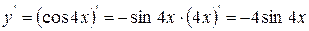
2) 

6. у= f(x), х є D, 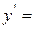

За властивістю границі маємо:
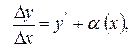 де
де 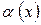 - нескінченно мала;
- нескінченно мала;

Доданок 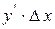 називається головною частиною приросту функції, її ще називають диференціалом функції:
називається головною частиною приросту функції, її ще називають диференціалом функції:
|
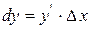
|
Геометричний зміст диференціала
Диференціал визначає приріст ординати дотичної, яка проведена в точці х0 до графіка функції у= f(x).
7. Інваріантність форми диференціала – незмінність: перший диференціал функції у= f(x) визначається за однією і тією самою формулою незалежно від того, чи змінна х є незалежною змінною, чи вона є функцією іншої змінної.
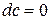
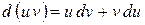

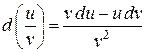
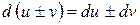
8. Диференціал функції застосовується в наближених обчисленнях.
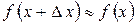
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 426; Нарушение авторских прав?; Мы поможем в написании вашей работы!