П Л А Н. 2. Опуклість і вгнутість кривих

Завдання додому.

1) Конспект; [1] с. 265, [2] с. 212-238.

Питання для самоконтролю

1. Екстремум функції.

2. Опуклість і вгнутість кривих.

3. Асимптоти кривої.

4. Схема дослідження функції та побудова графіка.

Л Е К Ц І Я 16

Тема: Функції багатьох змінних. Частинні похідні.

Мета: Сформувати поняття функції багатьох змінних; ознайомити з границею функції z=f (x; y), частинними та повним приростами функції z=f (x; y), частинними похідними.

Література: [1, с. 284-300]; [6, с. 276-307].

1. Означення функції багатьох змінних. Символіка.

2. Границя функції z=f (x; y).

3. Частинні та повний прирости функції z=f (x; y).

4. Частинні похідні.

1. Нехай задано множину D упорядкованих пар

y чисел (х; у).

y Означення. Якщо кожній парі значень (х; у) з

множини D за певним законом ставиться у відповідність

одне значення z, то говорять, що на множині D

0 х визначено функцію z від двох змінних х і у і записують

z=f (x; y)

Множина D є областю визначення функції z=f (x; y)

Способи задання функції:

1) символічний: z=f (x; y), z=F (x; y), z=z (x; y).

2) аналітичний: ;

3) табличний	у х	-2	-4	-5	z=xy;
	-1
	-3
	-5

5) графічний:

функція z=f (x; y) зображається у

z=f (x; y) вигляді поверхні, проекцією якої на

z площину Оху є множина D

y

D

x

Побудуємо: 1)

z

y

x

2) x² + y² + z²=1 – сфера

3) z=x² +y² - параболоїд обертання

z

y

х

2. Означення. Число А називається границею функції z=f (x; y) при і

, якщо для всіх пар значень (х; у), які як завгодно мало відрізняються від (х₀; у₀) відповідні значення функції як завгодно мало відрізняються від числа А.

Всі властивості і правила обчислення границі такі ж, як і для границь функцій однієї змінної.

3. Розглянемо функцію z=f (x; y), х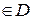, у.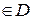

Нехай (х₀; у₀) – початкова точка, дамо приріст , а 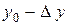. Одержимо нову точку .

Повним приростом функції z=f (x; y) називається різниця .

Якщо дати приріст тільки 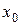, а 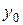залишити без зміни, то різниця

називається частинним приростом функції Z по аргументу х.

Аналогічно визначається частинний приріст функції Z по аргументу у:

4. Частинною похідною функції z по змінній х називається границя відношення частинного приросту функції по змінній х до приросту змінної х пр умові, якщо приріст аргумента х прямує до нуля.

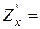
Аналогічно дається означення частинної похідної функції z по змінній у:

Частинні похідні позначаються символами:

, ; ;

, ; ;

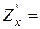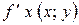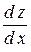Правила знаходження частинних похідних

1) Якщо знаходиться похідна по змінній х, то у є постійною величиною.

2) Якщо знаходиться похідна по змінній у, то х є постійною величиною.

Приклад:

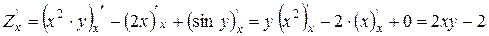
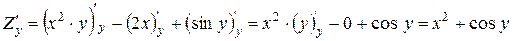
Дата добавления: 2014-01-04